Исследование методов оптимизации энергосбережения в электроприводах в системе ПЧ-АД
Автор: Мельничук Валерий Геннадьевич
Рубрика: 5. Энергетика
Опубликовано в
III международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2016)
Дата публикации: 31.03.2016
Статья просмотрена: 480 раз
Библиографическое описание:
Мельничук, В. Г. Исследование методов оптимизации энергосбережения в электроприводах в системе ПЧ-АД / В. Г. Мельничук. — Текст : непосредственный // Технические науки: теория и практика : материалы III Междунар. науч. конф. (г. Чита, апрель 2016 г.). — Чита : Издательство Молодой ученый, 2016. — С. 77-78. — URL: https://moluch.ru/conf/tech/archive/165/9975/ (дата обращения: 23.04.2024).
В данной статье рассматривается методика выбора параметров управляемого асинхронного электропривода, обеспечивающая снижение потери электроэнергии, используемых электроприводов. Решение задачи выбора параметров (синтеза) управляемого электропривода осуществляется на основе линеаризованной замкнутой системы ПЧ-АД.
Ключевые слова: асинхронный электропривод, математическая модель, обратная связь, система MATLAB, переходные процессы.
This article discusses methods of choosing the parameters of controlled asynchronous electric drive, ensuring the reduction of losses of electric energy used by electric motors. The selection of the parameters (synthesis) controlled drive is carried out based on the linearized closed-loop system FC-AD.
Key words: asynchronous electric drive, mathematical model, feedback, MATLAB, transients.
Промышленные электроприводы большинства производственных механизмов имеют завышенную мощность, превышающую в 2–3 раза необходимую и не соответствующую потребностям механизма, а средняя загрузка двигателей по отношению к установленной мощности не превышает 0,4–0,6 [1]. В связи с этим задача выбора параметров управляемого асинхронного электропривода, обеспечивающая снижение потери электроэнергии, является одной из необходимых задач минимизации затрат электроэнергии используемых электроприводов. Решение задачи выбора параметров (синтеза) управляемого электропривода осуществляется на основе линеаризованной замкнутой системы ПЧ-АД [2], структурная схема которой представлена на рисунке 1 в среде MATLAB.
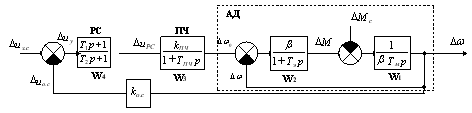
Рис. 1. Структурная схема системы ПЧ-АД
На схеме приняты следующие обозначения: β — модуль жесткости механической характеристики АД; Тэ — электромагнитная постоянная времени цепей статора и ротора АД; kПЧ — передаточный коэффициент функции ПЧ; ТПЧ — постоянная времени цепи управления ПЧ; Тм — электромеханическая постоянная времени.
Уравнение движения можно записать в следующем виде:
Дифференциальное уравнение электромагнитного момента запишется:
![]() .(2)
.(2)
Уравнение преобразователя частоты имеет вид:
![]() ,(3)
,(3)
А уравнение регулятора скорости запишется в следующем виде:
![]() .(4)
.(4)
Приращение ![]() запишем в следующем виде:
запишем в следующем виде:
![]() ,(5)
,(5)
где ![]() — приращение задающего сигнала;
— приращение задающего сигнала; ![]() — коэффициент обратной связи по скорости.
— коэффициент обратной связи по скорости.
Приведем вышеуказанные уравнения к задаче нелинейного программирования с ограничением на независимые переменные [3]. Для этого, производные переменных уравнений (1), (2), (3) и (4) приравниваем нулю. После несложных преобразований указанных уравнений мощность асинхронного двигателя, как функция многих переменных имеет следующий вид:
где![]() мощность асинхронного двигателя (символы приращения опущены);
мощность асинхронного двигателя (символы приращения опущены); ![]() напряжение на выходе регулятора скорости;
напряжение на выходе регулятора скорости; ![]() угловая скорость двигателя.
угловая скорость двигателя.
Ограничение на независимые переменные запишется в виде:
![]() (7)
(7)
здесь ![]() коэффициент обратной связи по скорости двигателя,
коэффициент обратной связи по скорости двигателя, ![]() задающий сигнал. Отметим, что в уравнениях (6) и (7) неизвестными параметрами являются коэффициент передачи преобразователя частоты и коэффициент обратной связи по скорости двигателя. С целью удобства решения поставленной задачи, задачи минимизации мощности асинхронного двигателя с одновременным определением численных значений коэффициентов преобразователя частоты и коэффициента обратной связи по скорости двигателя, введем замену переменных
задающий сигнал. Отметим, что в уравнениях (6) и (7) неизвестными параметрами являются коэффициент передачи преобразователя частоты и коэффициент обратной связи по скорости двигателя. С целью удобства решения поставленной задачи, задачи минимизации мощности асинхронного двигателя с одновременным определением численных значений коэффициентов преобразователя частоты и коэффициента обратной связи по скорости двигателя, введем замену переменных![]() В связи с этим уравнение (6) и (7), с параметрами двигателя 4А160М6У3 (15 кВт), принимают вид:
В связи с этим уравнение (6) и (7), с параметрами двигателя 4А160М6У3 (15 кВт), принимают вид:
![]() (8)
(8)
![]() (9)
(9)
где ![]() ограничение и
ограничение и![]() .
.
Программа решения задачи нелинейного программирования с неизвестными параметрами ![]() и
и![]() функции
функции ![]() и ограничения
и ограничения ![]() составленная на алгоритмическом языке системы MATLAB имеет вид:
составленная на алгоритмическом языке системы MATLAB имеет вид:
function Sintes_Parametrov
globalKpr; globalKoc; global T1; global T2;
disp('Программа метода сканирования');
h=0.1; e=0.01; f1=1e6;
Kpr=1/exp(rand)*20; Koc=1/exp(rand);
T1=1/exp(rand); T2=1/exp(rand);
x1=1; while x1<=100
x2=1; while x2<=50
g1=Koc*x1+x2;
if abs(g1-5)
f=abs(16.3*Kpr*x1*x2-16.3*x1^2);
if f<=f1 y1=x1;end
if f<=f1 y2=x2;end
end
x2=x2+h; end
x1=x1+h; end
disp('Результаты счета');
disp('f1='); disp(f1); m=0;
s1=0; s3=0; s5=0; s7=0;
for i=1:100
m=m+1;
s1=s1+Kpr; s2=sqrt(s1/m)^2; s3=s3+Koc;
s4=sqrt(s3/m)^2; s5=s5+T1; s6=sqrt(s5/m)^2;
s7=s7+T2; s8=sqrt(s7/m)^2;
end
Kpr=s2; disp('Kpr='); disp(Kpr)
Koc=s4; disp('Koc='); disp(Koc)
T1=s6; disp('T1='); disp(T1)
T2=s8; disp('T2='); disp(T2)
x0=[0;0;0;0]; interval=[0 2];
[T,X]=ode45(@systm,interval,x0);
plot(T,X(:,1)*4,'k-',T,X(:,2),'r-');
grid
function dx=systm(t,x)
Kpr=s2; T1=s6; Koc=s4; T2=s8; u=1;
dx=zeros(4,1);
dx(1)=0.61*x(2);
dx(2)=815*x(3)-815*x(1)-50*x(2);
dx(3)=1000*Kpr*x(4)-1000*x(3);
dx(4)=(1/T2)*5-((Koc/T1)/(1.63*T2))-(Koc/T2)*x(1);
end
end
Отметим, что в программе метод сканирования [4] используется для минимизации мощности двигателя. Для расчета кривых переходного процесса скорости и электромагнитного момента двигателя замкнутой системы ПЧ-АД, при полученных параметров ![]() и
и ![]() , в программе используется численный метод Рунге-Кутта [5]. По кривым переходного процесса визуально определяется качество переходных процессов и выбирается наиболее приемлемый процесс с позиции перерегулирования и времени регулирования системы. Численные значения начальных приближений искомых параметров задаются случайными числами. На рисунке 2 приведены переходные процессы скорости и электромагнитного момента системы ПЧ-АД, с рассчитанными параметрами
, в программе используется численный метод Рунге-Кутта [5]. По кривым переходного процесса визуально определяется качество переходных процессов и выбирается наиболее приемлемый процесс с позиции перерегулирования и времени регулирования системы. Численные значения начальных приближений искомых параметров задаются случайными числами. На рисунке 2 приведены переходные процессы скорости и электромагнитного момента системы ПЧ-АД, с рассчитанными параметрами ![]() и
и ![]() .
.
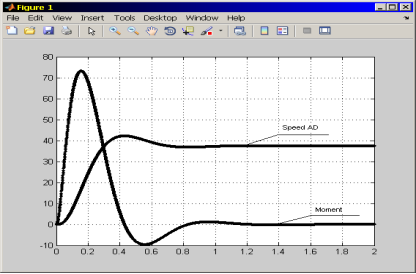
Рис. 2. Кривые переходного процесса скорости и момента асинхронного двигателя
Результаты счета:
Выводы. Перерегулирование и время регулирования, при расчитанных параметрах на ЭВМ в пределах нормы.
Литература:
- Браславский И. Я., Ишматов З. Ш., Поляков В. Н. Энергосберегающий асинхронный электропривод. — М.: Издательский центр «Академия», 2004. — 256 с.
- Терехов В. М., Осипов О. И. Системы управления электроприводов. — М.: Издательский центр «Академия», 2008. — 304 с.
- Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: Кн. 2. Пер. с англ. — М.: Мир, 1986. — 320 с.
- Бояринов А. И., Кафаров В. В. Методы оптимизации в химической технологии. — М.: Химия, 1975. — 576 с.
- Алексеев Е. Р., Чеснокова О. В. MATLAB 7. — М.: НТ Пресс. 2006. — 404 с.
Ключевые слова
математическая модель, переходные процессы, обратная связь, асинхронный электропривод, Система MATLAB, переходные процессы.Похожие статьи
Исследование нелинейной системы «Преобразователь частоты...»
Структурная схема нелинейной системы ПЧ-АД создана на основе линеаризованной системы ПЧ-АД с обратной связью по скорости [2]. Как видно из рисунка 1 в структурной схеме замкнутой нелинейной системы...
Анализ устойчивости замкнутой нелинейной системы...
В статье приведена линеаризованная структурная схема системы ПЧ-АД. Дается математическое описание замкнутой системы
Фазовая траектория замкнутой нелинейной системы «Преобразователь частоты — асинхронный двигатель» приведена на рисунке 3.
Исследование параметров управляющего устройства...
Рассматривается алгоритм синтеза параметров управляющего устройства асинхронного электропривода с системой преобразователь частоты — асинхронный двигатель на ЭВМ. Ключевые слова: асинхронный электропривод, преобразователь частоты, среда MATLAB...
Математическая модель САР скорости линейного асинхронного...
, гдеτ – полюсное деление линейного асинхронного двигателя (рассмотрим двухполюсную машину); fc – частота
% Программирование задатчика интенсивности Matlab-Script.
Замкнутая САР скорости линейного асинхронного двигателя показана на рис. 11.
Моделирование моментов нагрузки электродвигателей в MATLAB
Широко распространенным инструментом решения задач электромеханики является пакет «Matlab – Simulink», где
Асинхронный короткозамкнутый двигатель (Asynchronous Mashine) имеет следующие паспортные данные и параметры схемы замещения
Математическая модель САР скорости линейного асинхронного...
Замкнутая САР скорости линейного асинхронного двигателя показана на рис. 11.
График скорости и момента в замкнутой системе.
Функциональная схема модели САР скорости асинхронного двигателя в Matlab-Script.
Математическая модель асинхронного двигателя во...
Моделирование САР скорости асинхронного двигателя...
Программирование линейного асинхронного двигателя с числом... Рис. 1. а) Линейный асинхронный двигатель (2р = 2, Z1 = 6); б)
Функциональная схема модели САР скорости асинхронного двигателя в Matlab-Script.
Математическая модель электропривода на базе синхронного...
блок, ABC, асинхронный двигатель, векторное управление, параметр блоков, преобразователь координат, регулятор скорости, параметр блока, параметр
4. Нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
Исследования нелинейного корректирующего устройства...
Нелинейное корректирующее устройство замкнутой системы «Преобразователь частоты – асинхронный двигатель» с короткозамкнутым ротором аналогично звену переменной структуры.
Похожие статьи
Исследование нелинейной системы «Преобразователь частоты...»
Структурная схема нелинейной системы ПЧ-АД создана на основе линеаризованной системы ПЧ-АД с обратной связью по скорости [2]. Как видно из рисунка 1 в структурной схеме замкнутой нелинейной системы...
Анализ устойчивости замкнутой нелинейной системы...
В статье приведена линеаризованная структурная схема системы ПЧ-АД. Дается математическое описание замкнутой системы
Фазовая траектория замкнутой нелинейной системы «Преобразователь частоты — асинхронный двигатель» приведена на рисунке 3.
Исследование параметров управляющего устройства...
Рассматривается алгоритм синтеза параметров управляющего устройства асинхронного электропривода с системой преобразователь частоты — асинхронный двигатель на ЭВМ. Ключевые слова: асинхронный электропривод, преобразователь частоты, среда MATLAB...
Математическая модель САР скорости линейного асинхронного...
, гдеτ – полюсное деление линейного асинхронного двигателя (рассмотрим двухполюсную машину); fc – частота
% Программирование задатчика интенсивности Matlab-Script.
Замкнутая САР скорости линейного асинхронного двигателя показана на рис. 11.
Моделирование моментов нагрузки электродвигателей в MATLAB
Широко распространенным инструментом решения задач электромеханики является пакет «Matlab – Simulink», где
Асинхронный короткозамкнутый двигатель (Asynchronous Mashine) имеет следующие паспортные данные и параметры схемы замещения
Математическая модель САР скорости линейного асинхронного...
Замкнутая САР скорости линейного асинхронного двигателя показана на рис. 11.
График скорости и момента в замкнутой системе.
Функциональная схема модели САР скорости асинхронного двигателя в Matlab-Script.
Математическая модель асинхронного двигателя во...
Моделирование САР скорости асинхронного двигателя...
Программирование линейного асинхронного двигателя с числом... Рис. 1. а) Линейный асинхронный двигатель (2р = 2, Z1 = 6); б)
Функциональная схема модели САР скорости асинхронного двигателя в Matlab-Script.
Математическая модель электропривода на базе синхронного...
блок, ABC, асинхронный двигатель, векторное управление, параметр блоков, преобразователь координат, регулятор скорости, параметр блока, параметр
4. Нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
Исследования нелинейного корректирующего устройства...
Нелинейное корректирующее устройство замкнутой системы «Преобразователь частоты – асинхронный двигатель» с короткозамкнутым ротором аналогично звену переменной структуры.











