В данной статье разработан алгоритм шифрования по правилам криптосистемы RSA, а также описывается Windows-приложение, реализующее данный алгоритм.

Ключевые слова: шифрование, криптосистема RSA.

На данный момент в современном мире защита информации играет немаловажную задачу. Этой задачей обеспокоены не только крупные банковские системы и системы управления, но и простые пользователи. На помощь к решению такой задачи приходит наука криптография. Криптография — это наука о методах преобразования (шифрования) информации с целью защиты с использованием математических методов. Она приводит к сведению на минимум потерь в управлении, вызванных нарушением целостности данных, их конфиденциальности или доступности.

Криптография с открытым ключом. Криптосистема RSA

На основе открытий, сделанных Хелманом и Диффи в криптографии возникло новое направление называющееся криптография с открытым ключом.

Принципиальная разница данного подхода от использовавшихся ранее криптографических систем, заключается в использование двух разных алгоритмов для шифрования и дешифрования данных. В связи с этим такие шифры получили название асимметрические.

Криптосистема с открытым ключом составляют следующие элементы:

КЕ — открытый (незащищенный) ключ, используемый для шифрования данных.

КD — закрытый ключ, используемый для дешифрования данных

Е(m) — односторонняя функция позволяющая зашифровать открытый текст m с использованием ключа КЕ.

D(S) — односторонняя функция позволяющая дешифрованию шифр-текст S с использованием закрытого ключа КD

Очевидно, что D(Е(m))=m.

Строение криптосистемы RSA

Пусть имеется два пользователя, связанных друг с другом общественным каналом связи. Каждый пользователь в самом начале протокола выбирает два очень больших простых числа p и q. Определяется число n=p*q. Зная состав сомножителей числа n и несложно вычислить φ(n).

Затем пользователи получают случайное целое число е в диапазоне , такое, что: НОД

Отметим, что говоря о случайном выборе, мы подразумеваем, что число выбирается с помощью датчика случайно (псевдослучайных) чисел.

Таким образом пользователь А сгенерировал числа naи ea

такие, что:

В дальнейшем пользователь А вычисляет число da, обратное относительно умножения к , т. е.

В дальнейшем ключ шифрования Кea составляет пара чисел naи ea (отметим, что Кeaесть открытый ключ). А ключ дешифрования Кda составляет пара чисел naи da(закрытый ключ)

В этих терминах шифр преобразования есть отображение

Z/nZ -> Z/nZ

(полная система вычетов по модулю n) и определяется следующее выражением

а обратное дешифрование

Рассмотрим пример. Зашифровать с помощью алгоритма RSA сообщение «YES»

Будем считать, что открытый текст составлен из триграмм (по три символа), а шифр-текст состоит из четырехграмм (по 4 символа) 26 буквенного алфавита.

Определим в начале числовой эквивалент для открытого текста

Y E S

В дальнейшем используем ключ

pqe

и получаем по формуле

затем переводим в буквы, получаем:

передаем пользователю В полученное сообщение:

С=21166

Несмотря на кажущуюся простоту криптосистемы RSA анализ её устойчивости позволяет сделать вывод: стойкость RSA существенно зависит от выбора p и q. В частности при не удачном выборе этих параметров задача криптоанализа может быть решена за сравнительно малое время. Таким образом на p и q накладываются следующие ограничения:

а)                                                                                                                                                                                                                                                                                                                        эти простые числа не должны быть слишком близки друг к другу;

б)                                                                                                                                                                                                                                                                                                                        числа p-1и q-1должны иметь маленький НОД:

в)                                                                                                                                                                                                                                                                                                                        числа p-1и q-1должны иметь по очень большому делителю каждое.

Описание приложения

Так как данных подобных приложений не было найдено в свободном доступе, следует сделать его интуитивно простым, чтобы показать сущность алгоритма.

1.                Генерируем ключи с помощью кнопки «Сгенерировать ключи», далее в текстовое окно вводим слово MISHA, вычисляем числовой эквивалент и зашифровываем. (Рис.1)
2.                Проверяем правильность работы программы, используя кнопку «Дешифровать» и также получаем слово MISHA (Рис.2).

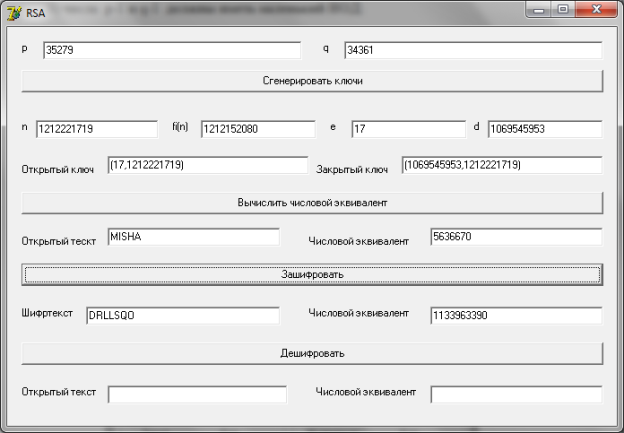
Рис.1. пример шифрования

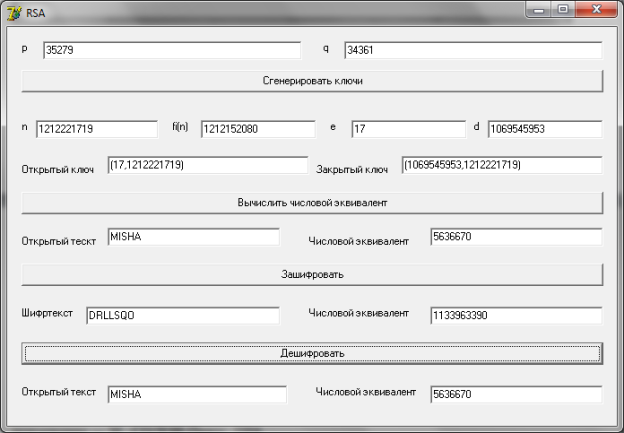
Рис.2. пример дешифрования

Данное приложение можно усовершенствовать, добавив разные языки для шифрования и дешифрования текста.

Литература:

1. Бунин О. Занимательное шифрование // Журнал «Мир ПК» 2003 № 7.
2. М. А. Иванов Криптография. Криптографические методы защиты информации в компьютерных системах и сетях, Изд. КУДИЦ-Образ,2001, ISBN: 5–93378–021–9
3. Лукашов И. В. Криптография? Железно! //Журнал «Мир ПК». 2003. № 3
4. Тарасюк М. В. Защищенные информационные технологии. Проектирование и применение — М.: СОЛОН-Пресс, 2004.
5. Партыка Т. Л., Попов И. И. Информационная безопасность. Учебное пособие для студентов учреждений среднего профессионального образования.— М.: ФОРУМ: ИНФРА-М, 2004.
6. С. Бернет, С. ПэйнКриптография. Официальное руководство RSA Security, Бином, 2002, ISBN: 5–9518–0003-Х