Исследование нелинейной динамической цепи с тиристорными элементами в системе электроснабжения

В статье рассмотрены исследование переходные процессы в нелинейных динамических цепях, приведено решение дифференциальных уравнений состояния численным методом в системе электроснабжения.

In article transition processes in nonlinear dynamic chains are considered research, the solution of the differential equations of a state by a numerical method is provided in system of power supply.

Необходимость повышения производительности труда и усложнения технических процессов обуславливает широкое применение на промышленных предприятиях силовых полупроводниковых устройств, которые позволяют осуществлять безударный пуск электродвигателей, ограничивают токи короткого замыкания и используются для уменьшения перенапряжения в момент коммутации.

При этом находят широкое применение нелинейные динамические цепи с тиристорами.

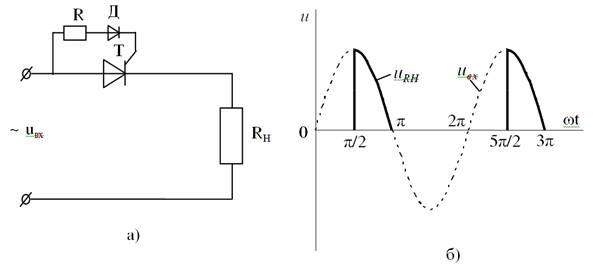
Рис. 1.

Рассмотрим цепь, когда тиристор последовательно подключается к сети через активное сопротивление, а в цепь управления подается ток из сети через активное сопротивление R и диод Д (рис.1.,а). В данной цепи угол открытия тиристора зависит от амплитуды управляющего сигнала. Если медленно повышать величину входного напряжения, то при определенном значении входного напряжения U₁, тиристор открывается при угле α=90⁰ (рис. 1.,б), дальнейшее увеличения напряжения приводит к уменьшению угла почти до нуля, т. е. тиристор будет пропускать полную положительную полуволну напряжения источника питания [1]. Величина напряжения при котором тиристор открывается скачком, зависит от величины параметров R и R_Н.

Для уменьшения пульсации на нагрузке R_Н подключим параллельно к нему емкость С (рис.2.,а).

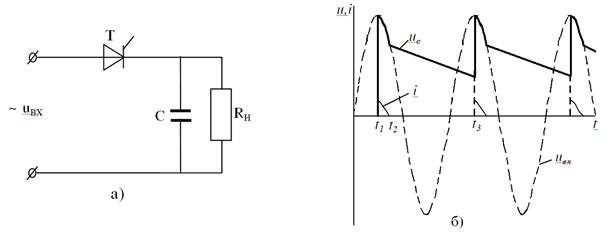
Рис. 2.

Проведем теоретический анализ неавтономной динамической цепи находящийся под воздействием внешнего синусоидального напряжения. Известны различные способы анализа таких цепей [2,3,4], нами для этой цели предлагается использовать численное решения уравнения состояния цепи. При этом необходимо определить на некотором отрезке приближенное решение уравнения:

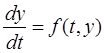                                                                                                             (1)

Допустим, что напряжение источника питания изменяется по синусоидальному закону и тиристор имеет идеальную характеристику.

Очевидно, что до момента t=t₁ тиристор будет закрыт, напряжение на емкости С будет равно нулю. В момент t=t₁ тиристор скачком открывается и к емкости С будет приложено напряжение:

,

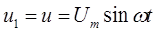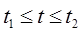
где, t₂–момент времени, когда ток протекающий через тиристор принимает нулевое значение.

Запишем выражение тока протекающего через тиристор:

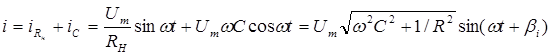         (2)

где, .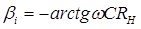

Ток обратится в нуль при 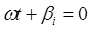 т. е. при .

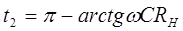В момент t₂ напряжение на емкости С будет равно напряжению источника, т. е. 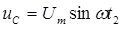, а тиристор Т закрыт, поэтому происходит разряд конденсатора на сопротивление R_Н. Для определения закона изменения напряжения на емкости необходимо решить следующее уравнение состояния цепи:

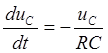                                                                                                            (3)

Определим значение u_c для различных точек от t₁до t₂ задаваясь шагом интегрирования h.

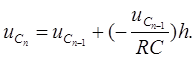                                                                                      (4)

На рис.2.,б представлен график напряжения на емкости, полученный численным решением уравнений 3.

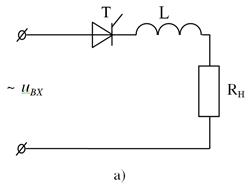
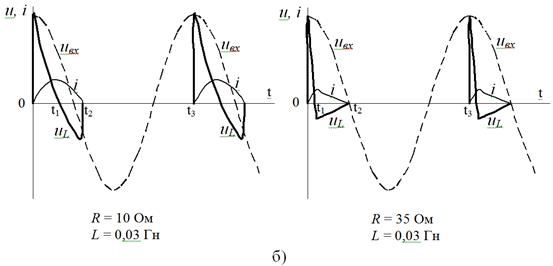
Рис. 3.

Рассмотрим цепь, состоящую из последовательно соединенных тиристора, индуктивной катушки и активного сопративления (рис.3.,а). Уравнение данной цепи, имеет следующий вид:

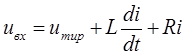                                                                                        (5)

Принимаем характеристику тиристора идеальной, тогда для открытого состояния тиристора уравнение 5 примет вид:

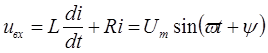
для :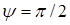

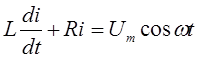                                                                                     (6)

Или

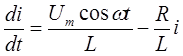                                                                                         (7)

Отсюда

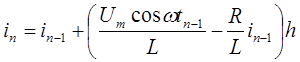                                                            (8)

На рис.3.б показаны кривые напряжения на зажимах элементов L и R и тока, построенных решением уравнения 7 численным методом с применением ЭВМ. Как видно из этого рисунка ток постепенно нарастает и происходит затягивание момента прекращения тока относительно момента перехода фазного напряжения через нулевое значение. Вид формы кривой тока зависит от соотношения параметров цепи L и R.

В заключении отметим, что анализ неавтономной динамической цепи, состоящей из тиристора, соединенного последовательно с параллельным контуром, включающим емкость и активное сопротивление, а также цепи состоящей из последовательно соединенных тиристора, индуктивности и активного сопротивления можно осуществить численным решением уравнений состояния цепи.

Предложенная методика позволяет производить качественный анализ установившихся режимов и переходных процессов цепей при различных вариациях параметров.

Литература:

1.      Кублановский Я. С., Тиристорные устройства., М.: Энергия., 1981 г.

2.      Шопен Л. В., Бесконтактные электрические аппараты автоматики., М.: Энергоатомиздат., 1986 г.

3.      Г. И. Атабеков «Нелинейные электрические цепи», часть 2, М., «Энегия», 1979, 81–87 с.

4.      П. Н. Матханов «Основы анализа электрических цепей», Высшая школа, М., 1977, 232–233 с.

5.      Т. М. Кадыров, У. З. Узаков, Д. Н. Касымова «Анализ электрических цепей методом численного решения уравнений состояния», Вестник ТашГТУ, № 2, Ташкент, 2005, 56–60 с.

6.      Усмонов Э. Г., Абдураимов Э. Х., Каримов Р. Ч., Нелинейная динамическая цепь с тиристором, Журнал: «Проблемы информатики и энергетики», Ташкент, 2006 г, № 2–3, стр. 37–41.