В работе представлен пакет расширения, реализованный авторами в рамках системы Mathematica и предназначенный для исследования модели безопасности Take-Grant. Приведено описание функций и команд, используемых в данном пакете.
Введение
Теоретические основы информационной безопасности могут быть описаны в виде схематических рисунков и математических выкладок, в то время как рассмотрение практически важных примеров требует применения компьютеров и специализированного программного обеспечения. Возникает проблема: как представить работающий метод в максимально наглядной форме. В данной статье рассматривается одна из классических моделей безопасности, получивших широкое распространение для систем с дискреционным разделением доступа — модель Take-Grant [1, 2]. Авторами описывается библиотека подпрограмм для исследования указанной модели, разработанная средствами системы компьютерной алгебры Wolfram Mathematica [3]. Библиотека представляет так называемый пакет расширения, дополняющий стандартный функционал среды Mathematica.
Авторы считают, что интеграция данного пакета расширения в образовательный процесс позволит организовать современный учебный материал, обеспечивающий студентов инструментарием самообучения и самоконтроля, позволит проводить интерактивные занятия с визуализацией разных сценариев работы модели Take-Grant. Выбор Wolfram Mathematica в качестве основы для создания пакета расширения обусловлен тем, что это универсальная система, которая осуществляет численные и символьные вычисления, помимо языка программирования и среды разработки, в стандартный пакет поставки входит обширная справочная система. Отличительной особенностью данной системы является очень гибкая работа со списками и возможность описания моделей в виде графов. Списки относятся к числу базовых структур данной системы [3], а графы предоставляют возможность наглядно продемонстрировать преобразования исследуемой модели. Это дает явное преимущество по сравнению с другими системами компьютерной алгебры касательно реализации модели Take-Grant.
1 Описание модели Take-Grant
Напомним основные положения классической модели Take-Grant [1, 2].
В рамках модели Take-Grant компьютерная система представляется совокупностью следующих компонент:
- множеством объектов доступа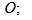 
- множеством субъектов доступа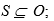 
- множеством прав доступа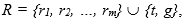 
где t (take) — право брать права доступа, g (grant) — право давать права доступа;
- конечный помеченный ориентированный без петель граф доступов, описывающий состояние системы — G = (S, O, E);
- множества S, О соответствуют вершинам графа;
- элементы множества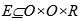 
представляют ребра графа, помеченные непустыми подмножествами из множества прав доступа R.
Состояние системы описывается соответствующим ему графом доступов. В данной модели возможно наличие прав доступа не только у субъектов к объектам, но и у объектов к объектам. Порядок перехода системы из состояния в состояние определяется правилами преобразования графа доступов, такими как:
1. Правило «Брать» — take(a,x,y,z). Субъект x берет права a у субъекта y на объект z;
2. Правило «Давать» — grant(a,x,y,z). Субъект x дает объекту y право α на доступ к объекту z;
3. Правило «Создать» — create(a,x,y). Субъект x создает объект y с правами доступа на него α ⊆ R;
4. Правило «Удалить» — remove(a,x,y). Субъект x удаляет права доступа α на объект y.
При выполнении данных правил происходит преобразование графа G0 в граф G1.
Передача прав между субъектами определяется с помощью предиката «Возможен доступ»(a,x,y,G0).
Основной задачей в рамках модели Take — Grant является задача о проверке возможности передачи прав данного субъекта другому субъекту. Указанная задача решается посредством необходимых и достаточных условий передачи права, выраженных в виде соответствующих теорем. В данной работе мы ограничимся приведением формулировки теоремы для случая, когда граф доступов содержит только вершины-субъекты. Предварительно введем следующее определение.
Определение 1. Вершины графа доступов являются tg-связными, если (без учета направления дуг) в графе между ними существует такой путь, что каждая дуга этого пути помечена t или g.
Теорема 1. Пусть G0= (S0, S0, Е0) — граф доступов, содержащий только вершины-субъекты. Тогда предикат «Возможен доступ»(a,x,y,G0) истинен тогда и только тогда, когда выполняются следующие условия:
Условие 1. Существуют субъекты s1,..., sm, такие, что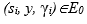 
для i = 1,...,m и
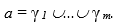
Условие 2. Субъект х соединен в графе G0 tg-путем с каждым субъектом si для i=1,...,т.
Приведенная нами теорема может быть обобщена и для произвольного графа доступов. При этом условия возможности передачи прав немного усложняются. Не приводя здесь окончательной формулировки, укажем лишь одно важное понятие, требуемое для проверки возможности передачи права.
Определение 2. Островом в произвольном графе доступов G0 называется его максимальный tg-связный подграф, состоящий только из вершин субъектов.
Выделение островов в графе доступов является важнейшей задачей, имеющей отношение к проблеме передачи прав субъектов.
2 Реализация модели Take-Grant в рамках системы компьютерной алгебры Mathematica
Исходя из описания модели Take-Grant, изложенного выше, нами была предложена следующая методика реализации данной модели.
Хотя модель отображается в элементах теории графов, для удобства ее можно представить и виде матрицы доступов. Т. к. субъекты могут быть объектами, а объекты могут иметь права на другие объекты, матрица доступов у нас будет квадратная. В процессе использования реализации модели всегда можно просмотреть текущее состояние системы. Это делается с помощью команды CurrentState. После выполнения данной команды выводятся матрица доступов и соответствующий ей граф (пример на рис. 1).
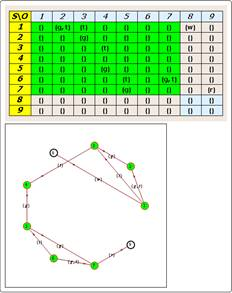
Рис. 1. Текущее состояние системы
В матрице доступов субъекты отображаются в начале списка и закрашены зеленым цветом, в графе номера вершин соответствуют матрице, и субъекты также закрашены зеленым цветом.
Пользователь должен иметь возможность задавать начальное состояние системы G0, т. е. создавать субъекты и объекты и устанавливать им права. Для этого нами реализованы следующие функции: CreateSubject, CreateObject и SetRight [SubjectNumber, ObjectNumber, Rights], где SubjectNumber –номер субъекта-объекта по матрице доступов, ObjectNumber — номер объекта по матрице доступов, Rights — предоставляемые права субъекту-объекту на объект (задается списком {g,r,t,w}). Указание фигурных скобок в данном параметре обязательно.
При создании субъекта или объекта в матрицу доступа добавляются строка и столбец, соответствующие новому элементу в системе, где строки — это субъекты-объекты, а столбцы — объекты. Вершина же в графе появится только после того, как субъекту-объекту будут даны какие-либо права на объект, и соответственно отобразиться ребро с этими правами.
Из рис. 1 видно, что в рамках приведенного нами примера в системе присутствуют 7 субъектов и 2 объекта. Каждому субъекту-объекту даны некоторые права на объекты.
Для удаления субъектов и объектов, создана функция RemoveElement[Elem],где Elem — номер субъекта или объекта в матрице прав доступов.
После задания начального состояния системы G0, пользователь может приступить к исследованию системы, преобразуя ее в граф G1 с помощью описанных выше правил. Суть модели Take-Grant дать ответ на вопрос: возможно ли субъектом получить некоторые права доступа на объект ранее не имеющего эти права?
Для реализации данных правил созданы соответствующие функции:
1. TakeRight [Rights, SubjectNumber, ObjectNumber1, ObjectNumber2], где Rights — права (задаются из списка {g,r,t,w}), SubjectNumber, ObjectNumber1, ObjectNumber2 — номера субъектов или объектов в матрице доступов или графе. Пояснение: SubjectNumber берет у ObjectNumber1 права Rights на ObjectNumber2 (Что→Кто→У_кого→На_что);
2. GrantRight [Rights, SubjectNumber, ObjectNumber1, ObjectNumber2]. Пояснение: SubjectNumber дает ObjectNumber1 права Rights на ObjectNumber2 (Что→Кто→Кому→На_что);
3. Create [SubjectNumber, Rights]. Пояснение: SubjectNumber создает объект с правами Rights на него. Объект добавляется в конец списка;
4. Удаление или изменение прав выполняется уже упомянутой ранее функцией SetRight [SubjectNumber, ObjectNumber, Rights]. Пояснение: у SubjectNumber удаляются (Rights={}) или перезаписываются (с исключением удаляемого) права Rights на ObjectNumber.
В дальнейшем из определений и теоремы все действия проводятся в TG-графе, который отображается с помощью функции tgGraph [Directed]. Для гибкости в некоторые функции авторами была добавлена возможность выбирать тип графа: ориентированный или неориентированный. Соответственно Directed — 1 или 0. На рис. 2 приведен пример неориентированного tg -графа.
Рис. 2. Неориентированный tg –граф системы
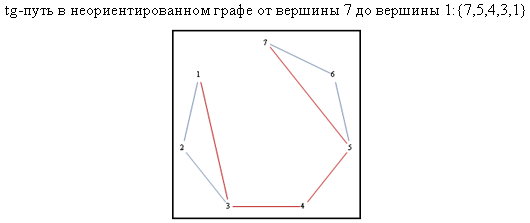
Рис. 3. Короткий путь в tg-графе между двумя вершинами
Для поиска короткого пути в tg-графе между двумя вершинами создана функция FindTG[SubjectNumber1, SubjectNumber2, Directed] (рис. 3).
Для отображения островов по определению 2 создана функция ShowIslandTG[Directed] (рис. 4).
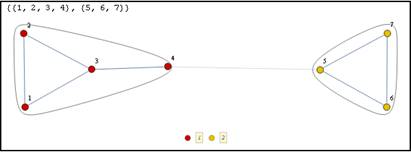
Рис. 4. Отображение островов системы
Также нами были созданы дополнительные функции, которые могут пригодиться для более глубокого исследования модели, например, TableDistance [Right, Directed], где Right принимает значение t или g. В результате выполнения данной функции выводится таблица длин коротких путей и граф, ребра которого имеют определенное право (рис. 5).
t — связь в неориентированном графе
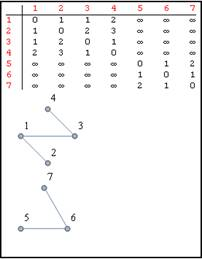
Рис. 5. Таблица длин коротких путей и граф с правом t
Заключение
В настоящей статье описан пакет расширения системы Mathematica, реализующий основные положения модели безопасности Take-Grant. Разработанная библиотека позволяет существенно расширить возможности изучения политик безопасности и повысить уровень и качество обучения студентов по соответствующим дисциплинам.
Литература:
1. Девянин П. Н. Модели безопасности компьютерных систем: Учеб. пособие для вузов. — М.: Академия, 2005. — 144 с.: ил.
2. Lipton R. J., Snayder L. A linear time algorithm for deciding subject security // Journal of ACM (Addison-Wesley). N.3. 1977. P.455–464
3. Computation meets knowledge. Wolfram Language & System. Documentation Center [Электронный ресурс]. URL: http://reference.wolfram.com/language/
