Интерполяция сплайнами 7-го порядка с дефектом 4

Пусть на плоскости OXY даны n опорных точек 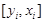, , 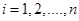интерполирующая функция  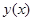удовлетворяет следующей системе уравнений

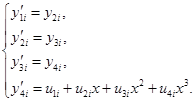                                                                                          (1)

Начальные условия для интегрирования имеют вид

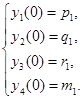
При этом 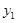 является описанием интерполирующей функции, 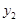,,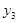 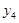- соответственно описаниями первой, второй и третьей производных функции; 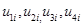- коэффициенты сплайна, которые необходимо определить. Решая систему (1), получаем окончательное описание функции и первых трех производных:

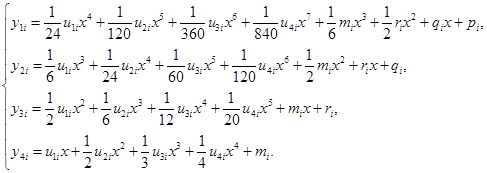                 (2)

Рассмотрим интерполирующую функцию на отрезке 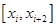 (рис. 1).

Обозначим 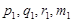 значения интерполирующей функции и первых трех ее производных на левом конце элементарного отрезка интерполяции, а 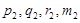,  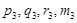— соответствующие значения в средней точке и на правом конце этого отрезка. Обозначим также ; , .

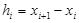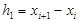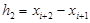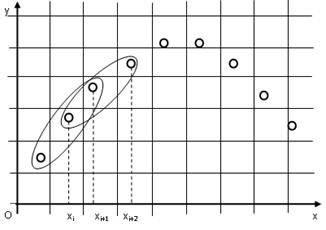
Рис. 1. Разбиение исходных точек на отрезки

 

Тогда для описанных условий система (2) для второй точки примет вид:

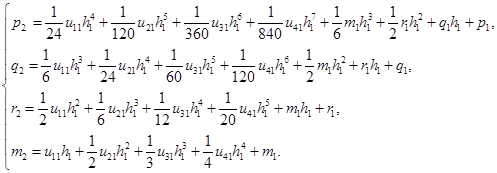
А для третьей точки вид:

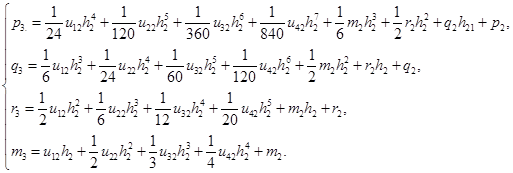
Система (2) в матричной форме ,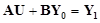

где ; ;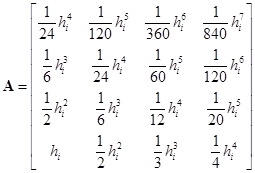

;      ;     .

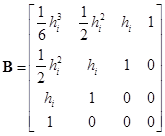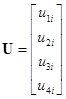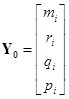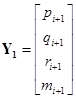Решение системы имеет вид:

.

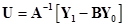Получим

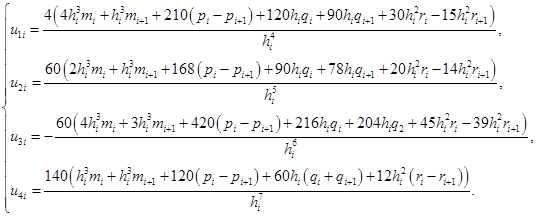
Выразим коэффициенты 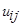 (i=1,2,3,4; j=1,2) через значения сплайна и его первых двух производных в граничных точках участков

При этом , .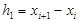

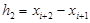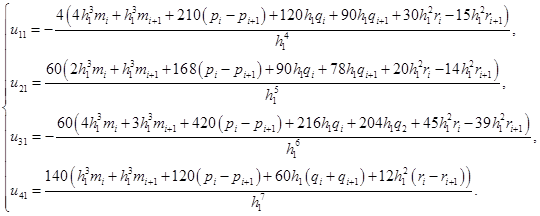    (3)

 

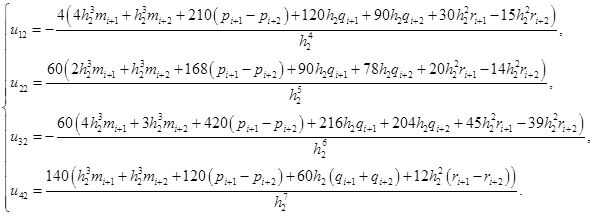     (4)

В качестве минимизируемой целевой функции будем использовать суммарный квадрат третьей производной, т. е. формально задача оптимизации имеет вид:

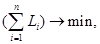
где 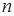 — количество элементарных отрезков интерполяции;

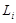- значение целевой функции (оценка кручения) на элементарном интервале интерполяции, определяемое по формуле:

,

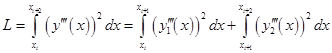С учетом системы (2), получим:

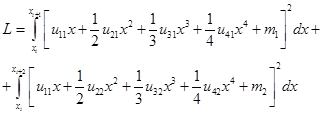                                                           (5)

Запишем выражение (5) в функциональной форме:

.

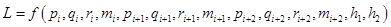Для определения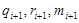, возьмем частные производные от L по переменным  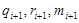и приравняем их к нулю:

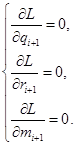
Решая данную систему, получим:

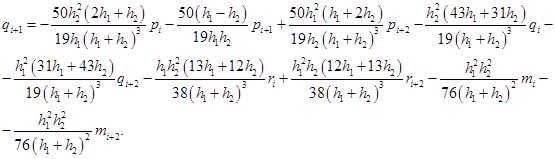
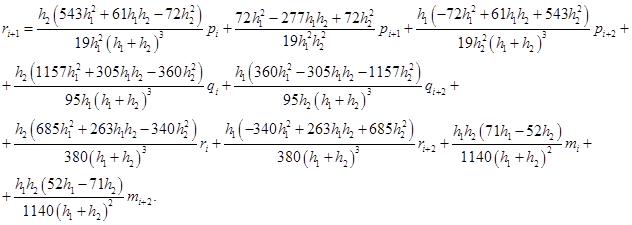
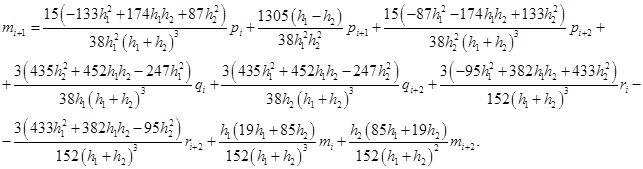
Подставляя полученные выражения в формулы (3) и (4) получим коэффициенты сплайна на отрезках .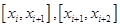

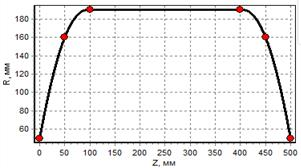
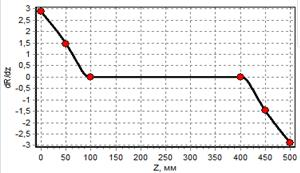
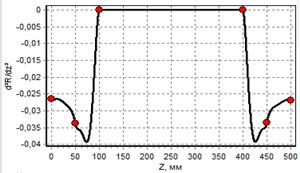
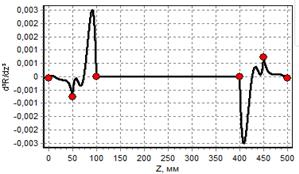
Результаты интерполяции исходных точек (образующая баллона наматывания) сплайнами 5 и 7 порядка представлены на рисунках 2 и 3. Из графиков видно, что сплайны 7-го порядка обеспечивают непрерывность третьей производной. Кроме того, сплайны 7-го порядка позволяют задавать значения как первых и вторых, так и третьих производных.

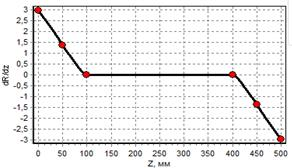
a)                  график функции	б) график первой производной
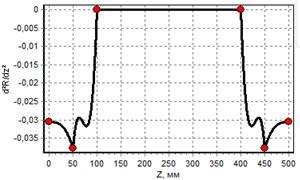
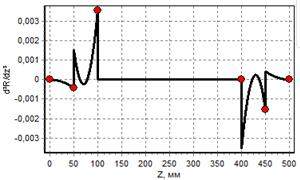
в) график второй производной	г) график третьей производной

Рис. 2. Графики для баллона, построенного сплайном 5-го порядка

 

а) график функции	б) график первой производной
в) график второй производной	г) график третьей производной

Рис. 3. Графики для баллона, построенного сплайном 7-го порядка

 

Литература:

 

1.                  Маринин В. И., Князев Д. Н. Интерполяция с использованием сплайнов пятого порядка. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. Спецвыпуск,– 2002.

2.                  Маринин В. И., Князев Д. Н. Использование сплайнов пятого порядка при построении образующих поверхностей вращения // Материалы Междунар. науч.-практ. конф. «Методы и алгоритмы прикладной математики в технике, медицине и экономике». Ч. 4. Новочеркасск, 2001.