Математическая модель композитного баллона, изготовленного непрерывной жгутовой намоткой
Авторы: Исаева Виктория Геннадьевна, Князев Дмитрий Николаевич
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015)
Дата публикации: 29.12.2014
Статья просмотрена: 786 раз
Библиографическое описание:
Исаева, В. Г. Математическая модель композитного баллона, изготовленного непрерывной жгутовой намоткой / В. Г. Исаева, Д. Н. Князев. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 118-122. — URL: https://moluch.ru/conf/tech/archive/124/7024/ (дата обращения: 20.04.2024).
В работе представлена модель композитного баллона давления изготавливаемого непрерывной жгутовой намоткой в виде системы дифференциальных уравнений, удобная для численного анализа, позволяющая получить конструкцию, образованную равнонапряженными нитями, уложенными вдоль геодезических линий на поверхности оправки.
Ключевые слова: композитный баллон давления, жгутовая намотка, геодезическая траектория, оптимальное армирование.
Рассмотрим композитный баллон давления в виде цилиндрической оболочки с днищами, выполненный методом намотки. Примем, что нить на днище совпадает с геодезической линией на поверхности (положение, которое нить стремится принять на гладкой поверхности при натяжении).
Под проектированием баллона давления будем понимать определение формы образующей баллона и схемы армирования баллона нитями. При этом оптимальным проектом является такой, который позволяет получить композитную конструкцию, образованную равнонапряженными нитями.
Как правило, при проектировании баллона давления в качестве исходных используют следующие данные (рис. 1):
— радиус оболочки на экваторе (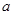 );
);
— радиус полюсного отверстия (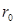 ).
).
Для геодезической намотки угол намотки на экваторе определяется по формуле:
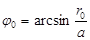 (1)
(1)
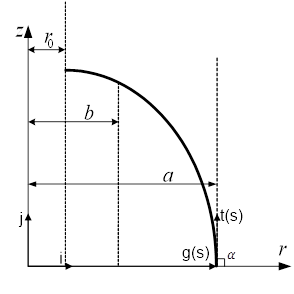
Рис. 1. — Профиль образующей днища: 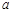 — радиус оболочки на экваторе;
— радиус оболочки на экваторе; 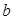 — максимальный радиус фланца;
— максимальный радиус фланца; 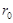 — радиус полюсного отверстия
— радиус полюсного отверстия
Принято [1, с.356; 2, с.54] искомую оптимальную форму образующей днища составлять из двух участков: участка от a до 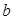 и участка от
и участка от 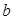 до
до 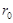 . При этом на первом участке форма днища определяется уравнением
. При этом на первом участке форма днища определяется уравнением
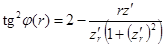 (2)
(2)
а на втором участке — уравнением
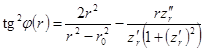 (3)
(3)
где 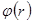 — угол намотки.
— угол намотки.
Уравнения (2) и (3) обеспечивают связь между углом намотки и формой образующей днища баллона для получения геодезической схемы армирования и равнонапряженности нитей в композитной конструкции.
Очевидным способом получения расчетной схемы на основе уравнений (2) и (3) является составление системы дифференциальных уравнений относительно 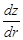 и
и 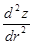 . Однако, возникает трудность с заданием начальных условий для интегрирования такой системы, поскольку в начальной точке — точке
. Однако, возникает трудность с заданием начальных условий для интегрирования такой системы, поскольку в начальной точке — точке 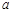 — значение производной
— значение производной 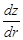 равно бесконечности (рис. 1).
равно бесконечности (рис. 1).
Получим систему дифференциальных уравнений используя натуральное уравнение плоской кривой [3, с.141]. Пусть 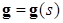 — плоская кривая, зависящая от натурального параметра
— плоская кривая, зависящая от натурального параметра 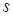 . Тогда можно записать:
. Тогда можно записать:
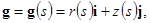
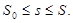
Условимся отсчитывать 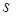 в положительном направлении, связанном с данной кривой. Произвольной остается только начальная точка отсчета.
в положительном направлении, связанном с данной кривой. Произвольной остается только начальная точка отсчета.
Обозначим через 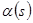 угол, образованный единичным касательным вектором [3]
угол, образованный единичным касательным вектором [3]
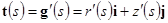
c положительным направлением оси 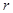 .
.
Тогда справедливы следующие равенства:
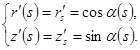 (4)
(4)
Найдем выражения для 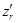 и
и 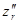 , входящих в (1) и (2), с учетом последних равенств:
, входящих в (1) и (2), с учетом последних равенств:
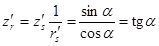
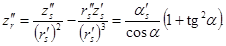
Окончательно получим:
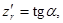 (5)
(5)
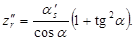 (6)
(6)
Подставляя (4) и (5) в (1) и выражая 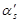 , получим:
, получим:
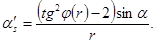 (7)
(7)
Объединяя уравнения (4) и (7), получим следующую систему дифференциальных уравнений для определения профиля днища и закона изменения угла намотки при 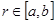 :
:
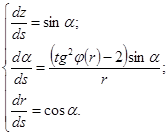 (8)
(8)
В этой системе дифференциальных уравнений начальный угол 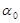 нельзя выбирать произвольно, так как
нельзя выбирать произвольно, так как 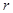 является функцией
является функцией 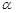 . Система (8) справедлива при
. Система (8) справедлива при 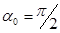 .
.
Аналогичным образом может быть получена система дифференциальных уравнений при 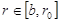 . Она имеет следующий вид:
. Она имеет следующий вид:
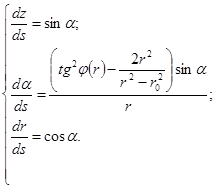 (9)
(9)
Решения систем (8) и (9) должны удовлетворять условиям сопряжения участков.
Результаты расчета профилей днищ представлены на рисунке 2, на котором профиль (1) соответствует радиусу на экваторе — 150мм, радиусу полюсного отверстия — 20мм, радиусу фланца (b1) — 24,5; профиль (2) соответствует радиусу на экваторе — 130, радиусу полюсного отверстия — 30, радиусу фланца (b2) — 36,75; профиль (3) соответствует радиусу на экваторе — 100, радиусу полюсного отверстия — 40, радиусу фланца (b3) — 49.
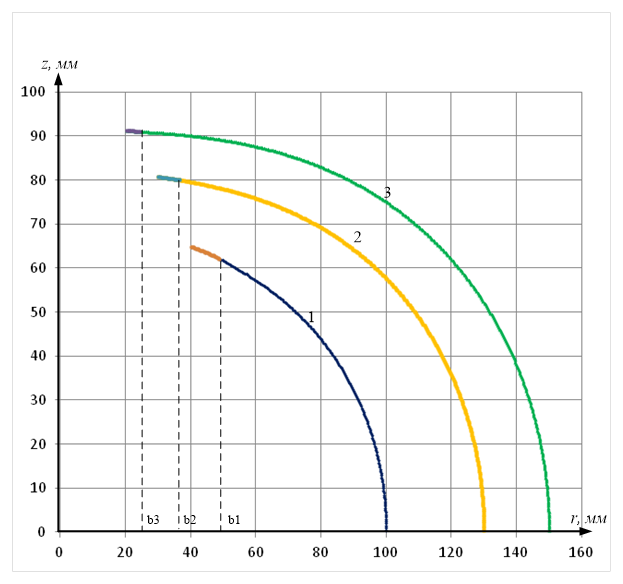
Рис. 2. Профили днищ
На рисунках 3, 4 и 5 представлены соответствующие трехмерные модели оболочек и их схемы армирования.
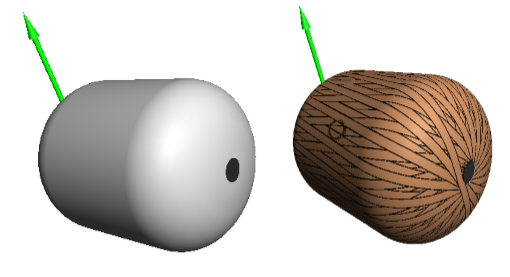
Рис. 3. Трехмерная модель оправки и схема армирования для профиля (1)
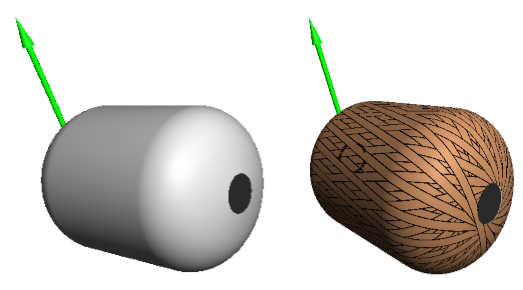
Рис. 4. Трехмерная модель оправки и схема армирования для профиля (2)
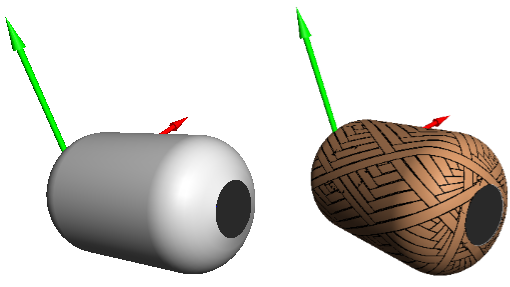
Рис. 5. Трехмерная модель оправки и схема армирования для профиля (3)
Литература:
1. Композиционные материалы: Справочник. — М.: Машиностроение, 1990.
2. В. В. Васильев, И. Ф. Образцов, В. А. Бунаков — Оптимальное армирование оболочек вращения из композиционных материалов методом намотки. — М., «Машиностроение», 1977.
3. П. К. Рашевский — Курс дифференциальной геометрии. Изд. 4-е, исправленное. — М.: Едиториал УРСС, 2003.
Ключевые слова
композитный баллон давления, жгутовая намотка, геодезическая траектория, опти-мальное армированиеПохожие статьи
Композитные материалы на основе углеродных волокон
Излишки смолы удаляются или вакуумформованием или давлением.
3. Намотка. Нить, ленту, ткань наматывают на цилиндрическую заготовку для изготовления труб.
Похожие статьи. Исследование электрических свойств композитного углеродного... Таблица.
Расчет сопряжения стенки цилиндрического резервуара с днищем...
Для составления расчетной схемы узла сопряжения из стенки и днища стального резервуара высотой H и радиусом R вырезаются полосы
Рис.2 Модель сваи в грунте.
При построении эпюры избыточного давления на плоские вертикальные и наклонные поверхности встречаются...
Применение композиционных материалов в конструкции БПЛА
При проектировании интегральных конструкций из композиционных материалов стараются реализовать следующие
выбор материалов и схем армирования с учетом величины и характера действующих нагрузок
Усиление металлических конструкций композитными...
Разработка методики выбора параметров армирования для...
Рис. 1. Трехосная схема армирования трубчатого элемента.
На рис. 2. показаны зоны и . Заметим, что по технологическим ограничениям угол армирования должен быть более 15о и объемное содержание
Исследование электрических свойств композитного углеродного...
Определение взаимосвязи сносов реакций опорной поверхности...
Полез-ные модели.
Статический радиус колеса: Давление колеса на опорную поверхность будет состоять из силы тяжести колеса , которая постоянна всем пятне контакта и силы созданной...
Моделирование точечного камуфлетного взрыва в грунте
, где - давление на границе полости взрыва, определяется следующим уравнением [3]
Результаты моделирования. Описанная выше схема реализована для расчета параметров
Рис. 4. Изменение радиуса камуфлетной полости взрыва и области дробления породы.
Использование технологии 3D-печати на этапе проектирования...
Основной конструктивной особенностью деталей семейства «Кронштейн» является схема базирования по двум отверстиям и базовой плоскости.
По большей части, в современные CAD-системы входят модули моделирования трехмерной объемной конструкции (детали) и...
Результаты расчета оценочных параметров устойчивости...
Углов разворота,̊ Пути, м. Торможение с АБС в правом повороте радиуса 35 м.
Определение линии действия эпюры давления колеса на опорную...
Параметрическая идентификация линеаризованных уравнений...
Моделирование распределения нагрузок по бандажной ленте...
В качестве исходного уравнения при моделировании методом систем с распределенными параметрами принято уравнение колебания
Рис. 1. Моделирование нагрузок давление пара и центробежных сил.
Рис. 2. График напряженности по радиусу и длине бандажной ленты.
Похожие статьи
Композитные материалы на основе углеродных волокон
Излишки смолы удаляются или вакуумформованием или давлением.
3. Намотка. Нить, ленту, ткань наматывают на цилиндрическую заготовку для изготовления труб.
Похожие статьи. Исследование электрических свойств композитного углеродного... Таблица.
Расчет сопряжения стенки цилиндрического резервуара с днищем...
Для составления расчетной схемы узла сопряжения из стенки и днища стального резервуара высотой H и радиусом R вырезаются полосы
Рис.2 Модель сваи в грунте.
При построении эпюры избыточного давления на плоские вертикальные и наклонные поверхности встречаются...
Применение композиционных материалов в конструкции БПЛА
При проектировании интегральных конструкций из композиционных материалов стараются реализовать следующие
выбор материалов и схем армирования с учетом величины и характера действующих нагрузок
Усиление металлических конструкций композитными...
Разработка методики выбора параметров армирования для...
Рис. 1. Трехосная схема армирования трубчатого элемента.
На рис. 2. показаны зоны и . Заметим, что по технологическим ограничениям угол армирования должен быть более 15о и объемное содержание
Исследование электрических свойств композитного углеродного...
Определение взаимосвязи сносов реакций опорной поверхности...
Полез-ные модели.
Статический радиус колеса: Давление колеса на опорную поверхность будет состоять из силы тяжести колеса , которая постоянна всем пятне контакта и силы созданной...
Моделирование точечного камуфлетного взрыва в грунте
, где - давление на границе полости взрыва, определяется следующим уравнением [3]
Результаты моделирования. Описанная выше схема реализована для расчета параметров
Рис. 4. Изменение радиуса камуфлетной полости взрыва и области дробления породы.
Использование технологии 3D-печати на этапе проектирования...
Основной конструктивной особенностью деталей семейства «Кронштейн» является схема базирования по двум отверстиям и базовой плоскости.
По большей части, в современные CAD-системы входят модули моделирования трехмерной объемной конструкции (детали) и...
Результаты расчета оценочных параметров устойчивости...
Углов разворота,̊ Пути, м. Торможение с АБС в правом повороте радиуса 35 м.
Определение линии действия эпюры давления колеса на опорную...
Параметрическая идентификация линеаризованных уравнений...
Моделирование распределения нагрузок по бандажной ленте...
В качестве исходного уравнения при моделировании методом систем с распределенными параметрами принято уравнение колебания
Рис. 1. Моделирование нагрузок давление пара и центробежных сил.
Рис. 2. График напряженности по радиусу и длине бандажной ленты.











