Треугольный конечный элемент с узловыми неизвестными в виде перемещений и их производных (функции формы для перемещений)
Авторы: Сорокина Елена Ивановна, Мелихов Константин Михайлович, Маковкина Лилия Николаевна
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015)
Дата публикации: 05.01.2015
Статья просмотрена: 648 раз
Библиографическое описание:
Сорокина, Е. И. Треугольный конечный элемент с узловыми неизвестными в виде перемещений и их производных (функции формы для перемещений) / Е. И. Сорокина, К. М. Мелихов, Л. Н. Маковкина. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 134-137. — URL: https://moluch.ru/conf/tech/archive/124/7004/ (дата обращения: 25.04.2024).
Приводятся расчет объемного конечного элемента треугольной формы поперечного сечения при различных вариантах аппроксимации перемещений.
Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации, перемещения, двумерный полином, матрица.
Если в качестве неизвестных в узле дискретного треугольного элемента принять и частные производные перемещений, то вектор узловых неизвестных конечного элемента с узлами i, j, k в глобальной системе координат будет иметь вид
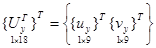 , (1)
, (1)
где
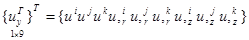 ;
;
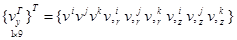 . (2)
. (2)
Для аппроксимации полей перемещений внутренних точек треугольного конечного элемента через узловые неизвестные обычно используется двумерный полином в локальной системе координат х, у. Полный двумерный полином содержит десять членов и имеет вид
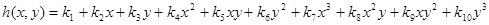 , (3)
, (3)
где коэффициенты ki являются неизвестными величинами, подлежащими определению.
Основная трудность при получении функций формы заключается в определении коэффициентов ki через компоненты вектора узловых неизвестных, так как число условий для определения коэффициентов ki всегда меньше их числа в полном двумерном полиноме(3). Поэтому приходится привлекать дополнительные условия.
Обоснованием корректности дополнительных условий являются результаты сопоставления на их основе приближенных решений с решениями других авторов или с точными решениями там, где это возможно.
В данной работе для определения коэффициентов аппроксимирующих полиномов дополнительным условием является добавление в столбец узловых неизвестных смешанной производной перемещения i-го треугольного конечного элемента 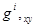 . Столбец узловых неизвестных в локальной системе координат имеет вид
. Столбец узловых неизвестных в локальной системе координат имеет вид
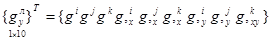 . (4)
. (4)
Перемещение внутренней точки конечного элемента выражается через узловые неизвестные величины соотношением
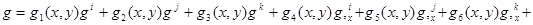
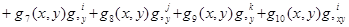 , (5)
, (5)
где под символом q понимается перемещение u или ν, а под символом qi(х, у)(i = 1…10) — аппроксимирующие функции формы.
Частные производные полного двумерного полинома (3) определяются выражениями
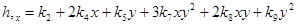 ;
;
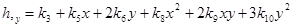 ;
;
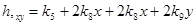 . (6)
. (6)
Для получения интерполяционных полиномов qn(х, у)(n = 1…10), составляется матричная зависимость вида
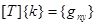 , (7)
, (7)
где
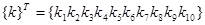 — столбец искомых коэффициентов, подлежащих определению для какой-либо одной функции qn(х, у);
— столбец искомых коэффициентов, подлежащих определению для какой-либо одной функции qn(х, у);
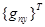 — матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой матрицы с номером n равен 1, остальные равны нулю). Например для функции q1(х, у) матрица-строка узловых значений имеет вид
— матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой матрицы с номером n равен 1, остальные равны нулю). Например для функции q1(х, у) матрица-строка узловых значений имеет вид
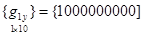 ,
,
для функции q4(х, у)
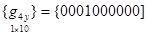 ,
,
а для функции q10(х, у)
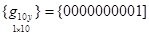 .
.
Элементы матрицы [T] представляют собой численные значения множителей при неизвестных коэффициентах ki полинома (1.3) и его производных (1.6) в узлах i, j, k конечного прямоугольного треугольника.
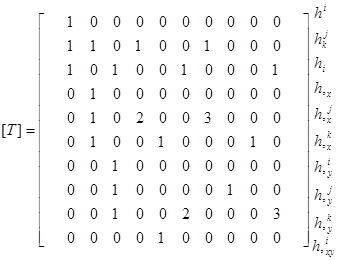 .
.
Решением системы уравнений для десяти столбцов 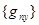 определяются коэффициенты km(m = 1…10) десяти аппроксимирующих функций q1(х, у), q2(х, у) … q10(х, у), входящих в (5).
определяются коэффициенты km(m = 1…10) десяти аппроксимирующих функций q1(х, у), q2(х, у) … q10(х, у), входящих в (5).
Смешанную производную перемещения узла i локального треугольника с использованием способа конечных разностей можно выразить через первые производные узловых перемещений по формуле
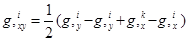 . (8)
. (8)
Если в локальной системе координат ввести вектор узловых неизвестных в виде
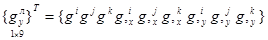 , (9)
, (9)
то на основании (8) между векторами 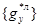 и
и 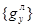 можно сформировать матричную зависимость
можно сформировать матричную зависимость
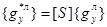 , (10)
, (10)
где матрица преобразования имеет вид
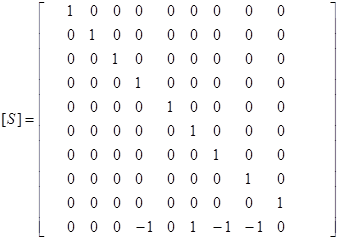 .
.
Перемещение внутренней точки конечного элемента с использованием узлового вектора (1.9) теперь можно аппроксимировать выражением
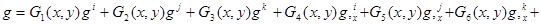
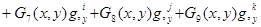 , (11)
, (11)
где под символом q по прежнему понимается перемещение u или осевое смещение ν, которые можно записать в матричном виде
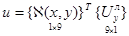 ;
;
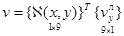 , (12)
, (12)
где строка 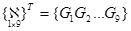 — матрица-строка аппроксимирующих функций.
— матрица-строка аппроксимирующих функций.
Аппроксимирующие полиномы Gi(x, y) (i = 1…9) определяются через полиномы qm(x, y) (m = 1…10) следующими выражениями [1]
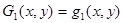 ;
; 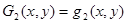 ;
;
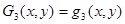 ;
; 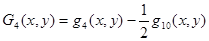 ;
;
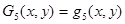 ;
; 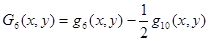 ;
;
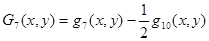 ;
;
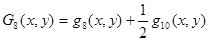 ;
;
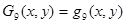 . (13)
. (13)
Окончательные выражения аппроксимирующих функций имеют следующий вид
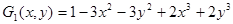 ;
;
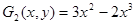 ;
;
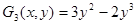 ;
;
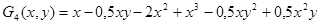 ;
;
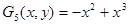 ;
;
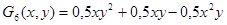 ;
;
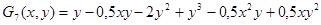 ;
;
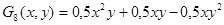 ;
;
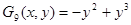 . (14)
. (14)
Частные производные перемещений внутренней точки конечного элемента определяются выражениями
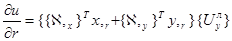 ;
;
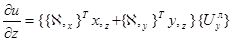 ;
;
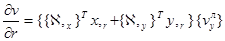 ;
;
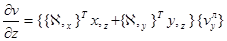 . (15)
. (15)
Литература:
1. Киселев, В. А. Строительная механика. Общий курс / В. А. Киселев. — М.: Стройиздат, 1986. — 520 с.
Ключевые слова
напряжения, перемещения, оболочка, деформации, матрица, объемный треугольный конечный элемент, несжимаемый материал, двумерный полиномПохожие статьи
конечный элемент, полный двумерный полином, локальная...
...координат, неизвестная, перемещение, выражение, вид, треугольный конечный элемент, двумерный полином, коэффициент.
конечный элемент, гидростатическое давление, неизвестная, локальная система координат, объемный конечный элемент, площадь...
Аппроксимация полиномов n степени методом наименьших...
Треугольный конечный элемент с узловыми неизвестными в виде... Столбец узловых неизвестных в локальной системе координат имеет вид. Частные производные полного двумерного полинома (3) определяются выражениями.
Комбинаторные приложения треугольника Паскаля
Треугольный конечный элемент с узловыми неизвестными... — матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой. . Решением системы уравнений для десяти столбцов определяются коэффициенты km(m.
Определение топологических компонентов диаграмм узловых...
Отсюда полином Джонса будет равен: Применяем другую форму записи полинома Джонса
Информационно-кибернетические исследования и проектирования сложных систем.
Алгоритмы формирования матрицы жесткости треугольного конечного элемента (краткий...
Алгоритмы формирования матрицы жесткости треугольного...
гидростатическое давление, треугольный конечный элемент, конечный элемент, площадь четырехугольника, поперечное сечение, объемный конечный элемент, неизвестная, координата, компонент вектора, вид...
Решение задач гидродинамики с помощью метода конечных...
Треугольный конечный элемент с узловыми неизвестными в виде... Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации, перемещения, двумерный полином, матрица.
Алгоритм получения матрицы жесткости четырехугольного...
конечный элемент, гидростатическое давление, неизвестная, локальная система координат, объемный конечный элемент, площадь четырехугольника, перемещение, матричная зависимость, осевое перемещение...
Многомерная интерполяция сеточной вектор-функции
Выпишем явные формулы для одномерной, двумерной, трехмерной интерполяции, записав выражения для относительных координат t1, t2
Вместе с тем для многих традиционных задач построения полиномов высоких степеней m, интерполирующих одной «глобальной» формулой...
К вопросу об алгоритмической сложности задачи Рейдемейстера
Множество важных инвариантов можно определить таким образом, включая полином
В сравнении с традиционным двумерным MOSFET-транзистором (МДП-транзистор основанный
При представлении графа обязательными являются 5 элементов структуры: имя графа (тип...
Похожие статьи
конечный элемент, полный двумерный полином, локальная...
...координат, неизвестная, перемещение, выражение, вид, треугольный конечный элемент, двумерный полином, коэффициент.
конечный элемент, гидростатическое давление, неизвестная, локальная система координат, объемный конечный элемент, площадь...
Аппроксимация полиномов n степени методом наименьших...
Треугольный конечный элемент с узловыми неизвестными в виде... Столбец узловых неизвестных в локальной системе координат имеет вид. Частные производные полного двумерного полинома (3) определяются выражениями.
Комбинаторные приложения треугольника Паскаля
Треугольный конечный элемент с узловыми неизвестными... — матрица-строка узловых значений функции qn(х, у) или ее производных (элемент этой. . Решением системы уравнений для десяти столбцов определяются коэффициенты km(m.
Определение топологических компонентов диаграмм узловых...
Отсюда полином Джонса будет равен: Применяем другую форму записи полинома Джонса
Информационно-кибернетические исследования и проектирования сложных систем.
Алгоритмы формирования матрицы жесткости треугольного конечного элемента (краткий...
Алгоритмы формирования матрицы жесткости треугольного...
гидростатическое давление, треугольный конечный элемент, конечный элемент, площадь четырехугольника, поперечное сечение, объемный конечный элемент, неизвестная, координата, компонент вектора, вид...
Решение задач гидродинамики с помощью метода конечных...
Треугольный конечный элемент с узловыми неизвестными в виде... Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации, перемещения, двумерный полином, матрица.
Алгоритм получения матрицы жесткости четырехугольного...
конечный элемент, гидростатическое давление, неизвестная, локальная система координат, объемный конечный элемент, площадь четырехугольника, перемещение, матричная зависимость, осевое перемещение...
Многомерная интерполяция сеточной вектор-функции
Выпишем явные формулы для одномерной, двумерной, трехмерной интерполяции, записав выражения для относительных координат t1, t2
Вместе с тем для многих традиционных задач построения полиномов высоких степеней m, интерполирующих одной «глобальной» формулой...
К вопросу об алгоритмической сложности задачи Рейдемейстера
Множество важных инвариантов можно определить таким образом, включая полином
В сравнении с традиционным двумерным MOSFET-транзистором (МДП-транзистор основанный
При представлении графа обязательными являются 5 элементов структуры: имя графа (тип...











