Модель сингулярного эстиматора частоты основного тона речи
Автор: Вольф Данияр Александрович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015)
Дата публикации: 20.12.2014
Статья просмотрена: 119 раз
Библиографическое описание:
Вольф, Д. А. Модель сингулярного эстиматора частоты основного тона речи / Д. А. Вольф. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 5-9. — URL: https://moluch.ru/conf/tech/archive/124/6961/ (дата обращения: 23.04.2024).
Применение аппарата сингулярного спектрального анализа для обработки речи. Разработана модель сингулярного эстиматора мгновенной частоты основного тона речи.
Ключевые слова: речь, фонема, модель, сингулярный спектральный анализ речи, сингулярное оценивание частоты основного тона.
Современные информационные технологии находят все более широкое применение в вычислительных и телекоммуникационных системах. Актуальной становится задача разработки и внедрения новых методов средств анализа информации для обеспечения потребителя максимальными данными об исследуемых объектах.
Предметом данной статьи является процесс оценивания одного из основных параметров устной речи — частоты колебаний голосовых связок при произнесении вокализованной речи, называемой основным тоном — F0 (величина обратная периоду T0 = 1/F0).
В настоящее время популярными алгоритмами оценивания частоты основного тона речевого сигнала являются RAPR, YIN и SWIPE’ Популярность перечисленных алгоритмов обусловлена хорошей функциональностью, низким процентом грубых ошибок и наличием свободно распространяемых версий их реализаций [1, с.49].
Большинство современных оценщиков основного тона состоят из трех основных модулей (рис. 1): 1 — модуль предобработки или приведения сигнала к требуемым характеристикам, 2 — генератор кандидатов действительного искомого периода основного тона, 3 — модуль постобработки или выбор наилучшего кандидата с последующим уточнением значения частоты основного тона.
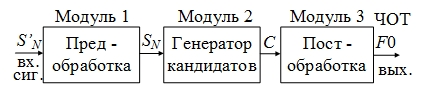
Рис.1.Схема типового оценщика основного тона
Главным недостатком подобных алгоритмов является зависимость от точности нахождения пиков. Наличие пиков и их амплитуда зависят от длины и вида окна анализа, а также от класса звука, что довольно часто приводит к ошибкам. Более того, точность зависит от значения частоты основного тона и от частоты дискретизации [9, с.16].
Еще одно ограничение обусловлено периодической (стационарной) моделью сигнала, лежащей в их основе, которая подразумевает точное повторение периода основного тона и не допускает его изменения на протяжении анализируемого фрейма. Например, при появлении модуляций –изменений частоты основного тона, точность оценок также существенно снижается.
В процессах исследования речевых сигналов, обычно используется математические аппараты спектрального анализа Фурье или вейвлет-анализ (wavelet-analysis). Однако в настоящей работе применен аппарат сингулярного спектрального анализа (ССА «Гусеница»), разработанного и обоснованного в конце 20 века сотрудниками Санкт-Петербургского государственного университета [7, с.5], [8, с.1]. Также в современной зарубежной литературе описан достаточно широкий класс методов, алгоритмически и идейно близких к методу «Гусеница», в основном метод известен как Singular Spectrum Analysis (SSA).
Метод основан на анализе главных компонент и позволяет исследовать стационарные и не стационарные временные ряды. Связь между классическими методами анализа стационарных временных рядов и методом главных компонент рассматривается в работах Бриллинджера [2, c.1].
Например, в работе Bagshaw [10, с.1] утверждается, что, методы, работающие во временной области, обладают наименьшей, по сравнению с другими методами (частотными), ошибкой принятия решения о присутствии голоса в речи (voicing decision error rate) –не более 17 %. Кроме того, в работе [11, с.399] показано, что такие методы являются наиболее робастными в отношении принятия решения о вокализованности или невокализованности сегмента речи в условиях шума (voiced-unvoiced decision), искажений и побочных помех в сигнале.
Результаты проводимых исследований в работах Вольф [3, с.114], [4, с.69] позволили построить модель процесса сингулярного оценивания мгновенной частоты основного тона речи, полученную модель предлагается рассмотреть ниже.
Концептуальная модель. Начнем с рассмотрения общего вида концептуальной модели сингулярного эстиматора основного тона речи (рис. 2):
1) Входные данные: SN — фонемный ряд гласных звуков речи длины N отсчетов с выборкой Fd кГц;
2) Выходные данные: F0 — частота основного тона речи, содержащаяся во временном кадре t мс; Amp — средняя амплитуда гармоники, соответствующая частоте основного тона речи; T0N — временной ряд, соответствующий квазигармонической составляющей (субфонеме) с частотой основного тона речи.

Рис. 2. Модель SEPT
Проведем декомпозицию обобщенной модели (рис. 3, 4):
1) Одномерный массив данных SN равностоящих значений (набор из квантов по уровню), полученных в результате дискретизации непрерывного множества S(t), поступает на вход системы осуществляющей расщепление в элементарный спектр временных рядов, генерируемых каждым резонатором речевого тракта. На выходе такой системы соответственно многомерный массив данных равностоящих значений TL,N — временной пучок (субфонемный спектр). Данный процесс эквивалентен классическому процессу генерации кандидатов искомого периода основного тона (рис. 1), однако в отличии от кросскорреляционных подходов в данном случае происходит генерация заранее известных функций (генератор сингулярных кандидатов частоты основного тона речи или генератора сингулярного спектра).
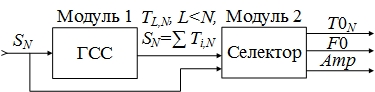
Рис. 3. Декомпозиция модели SEPT: SN — входной сигнал; TL,N — временной спектр; ГСС — генератор сингулярного спектра; SN — входной сигнал; T0N — трек с ЧОТ; F0 — ЧОТ; Amp — амплитуда.
2) Субфонемный спектр TL,N поступает на вход селектора и сохраняется в некотором блоке управления матрицы временного спектра (УМВС). Известно, что частота обертоновых составляющих речи кратна частоте основного тона, а также известны границы ее существования, таким образом ставиться задача уменьшения плотности временного пучка L до величины K, обеспечивая сужение границ поиска f0ϵ [fmin, fmax]. С помощью быстрого преобразования Фурье в блоке измерения частоты временного спектра (ИЧВС) осуществляется процесс измерения частотной характеристики элементов субфонемного спектра TL,N. На выходе блока измерения частоты временного спектра соответственно частотный ряд длины K, который поступает на вход блока выбора частоты основного тона (ВЧОТ). Далее решается задача выбора частоты основного тона речи из полученного спектра. В качестве критерия выбора ЧОТ взята наименьшая кратная величина частоты
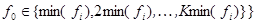 .
.
Ряд T0n вычисляется как процедура математической свертки. Далее на заданном промежутке времени (определяется N и частотой дискретизации) вычисляется средняя величина частоты основного тона F0 и амплитуда Amp.
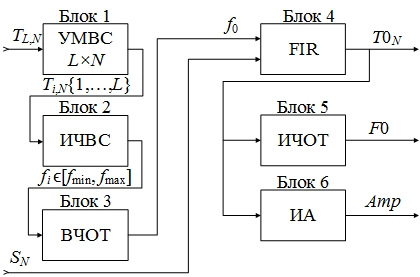
Рис. 4. Декомпозиция селектора модели SEPT: УМВС — блок управления матрицей временного спектра; ИЧВС — блок измерения частоты временного спектра; ВЧОТ — блок выбора ЧОТ; FIR — блок фильтрации; ИЧОТ — блок измерения ЧОТ; ИА — блок измерения амплитуды.
Математическая модель. Выше была рассмотрена концептуальная модель сингулярного эстиматора ЧОТ, теперь рассмотрим ее математическую интерпретацию в виде следующей системы:
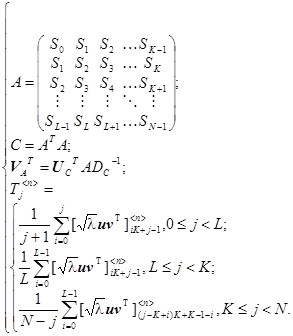 (1)
(1)
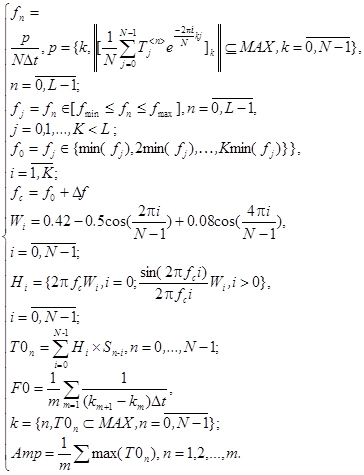 (2)
(2)
где:
(1) — математическая модель процесса, протекающего в генераторе сингулярного спектра (ГСС);
(2) — математическая модель процесса, протекающего в селекторе;
SN — исходный временной ряд;
N — длина ряда;
L — размер спектрального окна;
A — траекторная (Ханкелевая) матрица наблюдений;
C — бисимметричная матрица;
UC — левая сингулярная матрица поворота
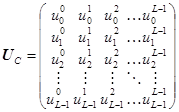 };
};
VAT — правая сингулярная матрица поворота;
u<n> — левый сингулярный вектор;
v<n> — правый сингулярный вектор;
D — диагональная матрица, состоящая из собственных значений λi бисимметричной матрицы C и края спектра значений исходной матрицы A
{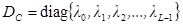 ,
, 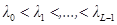 ;
;
Tin — спектр временных рядов (субфонемный спектр);
fn — одномерное, частотное представление временного спектра Tin при условии, что f0ϵ [fmin, fmax], где f0 — искомая частота основного тона такая, что
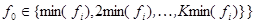
наименьшая кратная величина частоты;
p — индекс с максимальной амплитудой от преобразований Фурье в n-й квазигармонике (субфонеме);
∆t — частота дискретизации;
fc — частота среза;
Wi — ряд численно описывающий окно Блэкмена;
Hi — ряд численно описывающий конечно-импульсную характеристику фильтра нижних частот (ФНЧ);
T0N — временной ряд, соответствующий субфонеме с частотой основного тона речи;
F0 — средняя частота основного тона речи такая, что
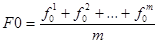 ,
,
где m — количество обратных величин равных периодам умещающихся в ряде T0N (f0m — мгновенная частота тона)
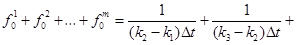 …
…
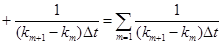 ,
,
где km — номер индекса в точке максимума
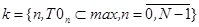 ;
;
Amp — средняя амплитуда гармоники (средняя величина по максимумам в ряде T0N) соответствующая частоте основного тона речи.
Система (1–2) описывает математическую модель процесса сингулярного оценивания частоты основного тона речи:
1) В (1) протекает процесс разложения исходного речевого сигнала (одномерного ряд) SN в спектр квазигармонических компонент (многомерный ряд) Tin, [i=0,1,…,N-1; n=0,1,…,L-1];
2) В (2) протекает процесс который решает следующие задачи:
- выбор одномерного ряда T0N, соответствующего частоте основного тона речи, из многомерного ряда Tin, соответствующего временному спектру;
- оценивается средняя частота основного тона речи F0 (с учетом модуляции), содержащаяся во временном ряде T0N;
- вычисляется средняя амплитуда временном ряде T0N.
Сингулярные матрицы UC и VA задают базис в линейном пространстве, порождаемый столбцами и строками исходной матрицы A.
Решение задачи сингулярного спектрального разложения одномерного временного ряда в многомерный (поиск величин u<n>, v<n>, λi) рассматривается в работах [5, с.81], [6, с.129].
Заключение. Рассмотрена модель процесса сингулярного оценивания мгновенной частоты основного тона речи. Данная модель описывает новый класс оценщиков частоты основного тона речи — сингулярный эстиматор частоты основного тона речи (singular estimator pitch tracking). Оценка адекватности и достоверности полученной модели требует дополнительной работы.
Литература:
1. Азаров И. С., Вашкевич М. И., Петровский А. А. Алгоритм оценки мгновенной частоты основного тона речевого сигнала / Цифровая обработка сигналов, № 4, 2012. —С.49–57.
2. Бриллинджер Д. Временные ряды. Обработка данных и теория. — М: Мир, 1980. —536 с.
3. Вольф Д. А. Выделение частоты основного тона речи методом сингулярного спектрального анализа / Системы управления и информационные технологии, № 2.1(56), 2014. —С.114–120.
4. Вольф Д. А. Автоматизация детектирования квазигармонических компонент, содержащих частоту основного тона речи в методе сингулярного спектрального анализа SSAPD / Системы управления и информационные технологии, № 3(57), 2014. — С.69–75.
5. Вольф Д. А. Программная реализация подсистемы быстрого сингулярного спектрального анализа речи // Системы управления и информационные технологии, № 4(54), 2013. —С. 81–86.
6. Вольф Д. А. Спектральная теорема для решения частичной проблемы собственных чисел степенным методом в задачах сингулярного спектрального анализа речи / Системы управления и информационные технологии, № 3.1(57), 2014. — С.129–135.
7. Голяндина Н. Э. Метод «Гусеница» — SSA: анализ временных рядов / Учебное пособие / Санкт-Петербург, 2004. — C.5–6.
8. Данилов Д. Л., Жиглявский А. А. Главные компоненты временных рядов: метод «Гусеница» / Под ред. Д. Л. Данилова, А. А. Жиглявского / СПб: Пресском, 1997. —308 с.
9. Конев А. А. Модель и алгоритмы анализа и сегментация речевого сигнала / Диссертация на соискание ученой степени кандидата технических наук по специальности 05.13.18 математическое моделирование, численные методы и комплексы программ / Федеральное агентство по образованию РФ. Томский государственный университет систем управления и радиоэлектроники: Томск, 2007. —128 с.
10. Bagshaw P. C. Automatic prosodic analysis for computer aided pronunciation teaching / Univ. of Edinburgh, Edinburgh. PhDThesis 1994 / — [Электронный ресурс] — Режим доступа. — URL: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.55.3401 (дата обращения: 30.11.2014).
11. Rabiner L. R., Cheng M. J., Rosenberg A. E. A comparative study of several pitch detection algorithms / IEEE Trans. Acoust. Speech, № 24, 1976. — Р. 399–423.
Ключевые слова
модель, речь, фонема, сингулярный спектральный анализ речи, сингулярное оценивание частоты основного тона., сингулярное оценивание частоты основного тонаПохожие статьи
Построение концептуальной модели сингулярного эстиматора...
Основные термины (генерируются автоматически): основной тон речи, основной тон, SEPT, временный спектр, сингулярный спектральный анализ, концептуальная модель процесса, речевой сигнал, сингулярное оценивание, частота, входной сигнал.
Обработка данных геомониторинга на основе сингулярного...
Модель сингулярного эстиматора частоты основного тона речи. SN — исходный временной ряд; N — длина ряда; L — размер спектрального окна; A — траекторная (Ханкелевая) матрица наблюдений.
Выделение границ фонем речевого сигнала с помощью...
Модель сингулярного эстиматора частоты основного тона речи. Ключевые слова: речь, фонема, модель, сингулярный спектральный анализ речи. В процессах исследования речевых сигналов, обычно используется математические.
Анализ математических моделей речевого тракта
Модель сингулярного эстиматора частоты основного тона речи. Разработана модель сингулярного эстиматора мгновенной частоты основного тона речи. Предметом данной статьи является процесс оценивания одного из основных параметров устной речи...
Подходы к выделению речи из исходного сигнала для системы...
Модель сингулярного эстиматора частоты основного тона речи. Разработана модель сингулярного эстиматора мгновенной частоты основного тона речи. В процессах исследования речевых сигналов, обычно используется математические аппараты...
Сегментация, шумоподавление и фонетический анализ в задаче...
Модель сингулярного эстиматора частоты основного тона речи. Ключевые слова: речь, фонема, модель, сингулярный спектральный анализ речи, сингулярное оценивание частоты основного тона.
Применение метода кросс-вейвлетов для анализа финансовых...
Модель сингулярного эстиматора частоты основного тона речи. В процессах исследования речевых сигналов, обычно используется математические аппараты спектрального анализа Фурье или вейвлет-анализ (wavelet-analysis).
Статьи по ключевому слову "сингулярный спектральный анализ...
Построение концептуальной модели сингулярного эстиматора мгновенной частоты основного тона речи. IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015) — Вольф Д. А.
Предварительная обработка речевых сигналов для системы...
Построение концептуальной модели сингулярного эстиматора... 1) Разложение исходного речевого сигнала в спектр квазигармонических компонент (задача 1); 2) Выбор квазигармонической составляющей соответствующей частоте основного тона речи (задача 2).
Похожие статьи
Построение концептуальной модели сингулярного эстиматора...
Основные термины (генерируются автоматически): основной тон речи, основной тон, SEPT, временный спектр, сингулярный спектральный анализ, концептуальная модель процесса, речевой сигнал, сингулярное оценивание, частота, входной сигнал.
Обработка данных геомониторинга на основе сингулярного...
Модель сингулярного эстиматора частоты основного тона речи. SN — исходный временной ряд; N — длина ряда; L — размер спектрального окна; A — траекторная (Ханкелевая) матрица наблюдений.
Выделение границ фонем речевого сигнала с помощью...
Модель сингулярного эстиматора частоты основного тона речи. Ключевые слова: речь, фонема, модель, сингулярный спектральный анализ речи. В процессах исследования речевых сигналов, обычно используется математические.
Анализ математических моделей речевого тракта
Модель сингулярного эстиматора частоты основного тона речи. Разработана модель сингулярного эстиматора мгновенной частоты основного тона речи. Предметом данной статьи является процесс оценивания одного из основных параметров устной речи...
Подходы к выделению речи из исходного сигнала для системы...
Модель сингулярного эстиматора частоты основного тона речи. Разработана модель сингулярного эстиматора мгновенной частоты основного тона речи. В процессах исследования речевых сигналов, обычно используется математические аппараты...
Сегментация, шумоподавление и фонетический анализ в задаче...
Модель сингулярного эстиматора частоты основного тона речи. Ключевые слова: речь, фонема, модель, сингулярный спектральный анализ речи, сингулярное оценивание частоты основного тона.
Применение метода кросс-вейвлетов для анализа финансовых...
Модель сингулярного эстиматора частоты основного тона речи. В процессах исследования речевых сигналов, обычно используется математические аппараты спектрального анализа Фурье или вейвлет-анализ (wavelet-analysis).
Статьи по ключевому слову "сингулярный спектральный анализ...
Построение концептуальной модели сингулярного эстиматора мгновенной частоты основного тона речи. IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015) — Вольф Д. А.
Предварительная обработка речевых сигналов для системы...
Построение концептуальной модели сингулярного эстиматора... 1) Разложение исходного речевого сигнала в спектр квазигармонических компонент (задача 1); 2) Выбор квазигармонической составляющей соответствующей частоте основного тона речи (задача 2).











