Применение экстремальных значений интеграла Шоке при принятии решений по оптимизации распределения инновационных ресурсов предприятий
Автор: Лавриченко Олег Вячеславович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015)
Дата публикации: 18.11.2014
Статья просмотрена: 160 раз
Библиографическое описание:
Лавриченко, О. В. Применение экстремальных значений интеграла Шоке при принятии решений по оптимизации распределения инновационных ресурсов предприятий / О. В. Лавриченко. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 9-14. — URL: https://moluch.ru/conf/tech/archive/124/6501/ (дата обращения: 20.04.2024).
Показана актуальность инновационных самоорганизующихся бизнесобразующих технологий в современных условиях экономического развития России. Рассмотрены основы авторской теории экономики активного коннекта. Обоснована необходимость снижения действия антропогенных факторов на эффективность аддитивных моделей и алгоритмов принятия решений. Показана необходимость экононормирования антропогенных сукцессий в рамках концепции сбалансированного распределения инновационных ресурсов промышленных предприятий между объектами инноваций. Исследованы существующие подходы к задаче оптимизации интеграла Шоке и возможности его применения при принятии решений для устранения диспаритета в распределении инновационных ресурсов между объектами инноваций.
Ключевые слова:инновационные ресурсы; экономика активного коннекта; антропогенные факторы; антропогенные сукцессии; инновационные самоорганизующиеся бизнесобразующие технологии; интеграл Шоке.
Информационные и когнитивные технологии входят в перечень критических технологий современной России, определенный в Указе Президента России № 899 от 7 июля 2011 года, а также являются приоритетными направлениями развития науки, технологий и техники согласно «Прогнозу научно-технологического развития Российской Федерации на период до 2030 года».
К информационным технологиям относятся и инновационные самоорганизующиеся бизнесобразующие технологии (ИСБОТ), являющиеся эндогенной основой авторской научной концепции сбалансированного распределения инновационных ресурсов между объектами инноваций.
Простые инновационные бизнесобразующие технологии были рассмотрены нами в ранее опубликованных работах [1], были определены не только как алгоритм действий по внедрению идеи, но и как технологии общения между участниками процесса реализации инновационной стратегии развития промышленного предприятия, методики обмена и структурирования информации между ними. Это способ общения и формирования не только инновационных стратегий, но и информационного сознания. Их можно описать как в виде сокращенного алгоритма, в виде элементарной понятийной схемы, состоящей из минимального количества элементов, так и создать в подробнейшем самосовершенствующемся мультимедийном формате. Идеальная инновационная бизнесобразующаяся технология — это самосовершенствующийся цифровой организм, интерактивная модель в структуре интеграционной модели реализации инновационной стратегии развития [2].
Основы авторской теории экономики активного коннекта
В современных условиях экономического развития России, характеризующихся усиливающимися санкционными мерами стран ЕС и США, особую роль приобретают технологии более высокого уровня — уровня самоорганизации. Характерной чертой самоорганизующейся инновационной бизнесобразующей технологии (ИСБОТ) является капитализация интеллектуального «сырья» в виде идей и действий, которые необходимо совершить для получения новых инноваций или нового знания, то есть они призваны не только отвечать на вопросы, но и формировать их, отправляя импульсы организаторам инновационных процессов на промышленном предприятии. Участники, включенные в процесс реализации инновационных стратегий развития, совместно принимают решение, а также вносят необходимые изменения в раздел инновационных бизнесобразующих технологий, за который он отвечает. [3] Таким образом, путем обмена информацией происходит принятие управляющего решения. Инновационные самоорганизующиеся бизнесобразующие технологии (ИСБОТ) как средство корпоративного общения и технологии обмена информацией способны создавать новое знание постоянно, да еще и в полуавтоматическом режиме.
Таким образом, в инновационных самоорганизующихся бизнесобразующих технологиях (ИСБОТ) отражены все возможные модели и алгоритмы действий по созданию объектов инноваций, их брендингу, производству и выводу на рынок. То есть, это системообразующий многоуровневый гипертекст, заключенный в форму четкой и понятной интерактивной инструкции. [4]
Как нами было уже неоднократно сказано [5], новая экономика — это не просто экономика информации или экономика коммуникаций (от латинского- делаю общим, контакт, связь, то есть подразумевает линии как материального, так и информационного обеспечения того или иного объекта). Это уже экономика коннекта (коннект в переводе с английского означает: соединять, устанавливать взаимоотношения, налаживать контакты, связываться, соединяться, ассоциировать, то есть ставить в причинную связь, быть согласованными, устанавливать непосредственную связь и т. д.).
Таким образом, концепция самоорганизующихся инновационных бизнесобразующих технологий (ИСБОТ) потребовала от нас своего исследования не только в ином направлении экономической мысли, но и выявила необходимость разработки данного направления как самостоятельной области экономических знаний — экономической теории активного коннекта (эконоконнекта).
Термин «теория экономики активного коннекта» впервые был введен автором [6] и до сих пор пока не применялся, однако в современной экономической науке потребность в нем имеется уже давно и его необходимо воспринимать как изменение в современных российских условиях не только характера труда, но и всего социума.
Теория экономики активного коннекта — это целостная, развивающаяся система знания, исследующая хозяйственную деятельность человека, которая предусматривает широкое применение информационных и когнитивных технологий в процессах производства, распределения и потребления общественных благ.
Актуальность авторского подхода — в возможности снизить действие неопределенности антропогенных факторов как основных факторов неустойчивости аддитивных моделей и алгоритмов. За счет чего? За счет увеличения инвестиций на разработку саморазвивающихся инновационных бизнесобразующих технологий (ИСБОТ), одной из целей которых является экононормирование антропогенных факторов, так как трансакционные издержки не должны превышать размер выгод от решения проблем внешних воздействий на аддитивные модели и алгоритмы.
Новизна авторского подхода заключается в необходимости учета трансакционных издержек длительности и интенсивности информационного активного коннекта между сотрудниками всех уровней и на всех итерациях процесса реализации интеграционной модели на основе инновационных самоорганизующихся бизнесобразующих технологий ИСБОТ). Источник этих трансакционных издержек — асиммитричность информационного активного коннекта между разработчиками интеграционной модели и ее реализаторами на всех итерациях.
Основную идею теории экономики активного коннекта (эконоконнекта) мы определяем как эндогенный информационно-коннектный подход к поведению сотрудников предприятия при реализации ими интеграционной модели реализации инновационной стратегии устойчивого развития с целью достижения им конкурентноспособности и возможности максимизации стоимости предприятия. [7]
Фундаментальная характеристика теории экономического коннекта — антропогенные факторы, влияющие прямо или косвенно на эффективность процессов формирования, реализации и саморазвития инновационных бизнесобразующих технологий. Антропогенные факторы опосредуются через кадровые ресурсы, задействованные в интегрированной модели реализации инновационной стратегии устойчивого развития промышленного предприятия. [8]
Результат негативного влияния антропогенных факторов — антропогенные сукцессии. Для ограничения их влияния необходима разработка мониторинга или их экононормирование, которое автор предложил осуществлять в рамках концепции сбалансированного распределения инновационных ресурсов между объектами инноваций.
Данный аспект проблемы автор уже рассматривал с позиций многомерных структур неоднородной совокупности на основе случайных выборок [9] и отношения Парето [10].
На наш взгляд, задачи принятия решений для оптимального распределения инновационных ресурсов между объектами инноваций перспективно рассматривать, применяя методы поиска экстремальных значений интеграла Шоке.
Интеграл Шоке в задачах принятия решений
Существующие подходы к задаче оптимизации интеграла Шоке в современных исследованиях.
До настоящего времени основная часть исследований по оптимизации интеграла Шоке была посвящена решению многокритериальных версий задач комбинаторной оптимизации. Так, например, в статье Галанда Л. и его коллег [11] рассматриваются задачи минимального покрывающего дерева в поисках кратчайшего пути в графах, где каждое ребро имеет несколько весов. Получающееся в результате дерево (путь) таким образом характеризуется некоторым вектором. Для того, чтобы выбрать из различных вариантов наилучший, авторы предлагают использовать интеграл Шоке для агрегации таких векторов в интегральные оценки. Таким образом, задача формулируется как задача минимизации интеграла Шоке на дискретном множестве. Авторы предлагают метод ветвей и границ, где верхняя грань вычисляется с помощью следующего свойства:
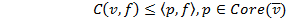
где 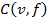 - интеграл Шоке по некоторой емкости
- интеграл Шоке по некоторой емкости 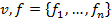 - функции весов,
- функции весов, 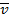 — емкость, сопряженная к
— емкость, сопряженная к 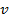 , то есть
, то есть 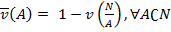 , и
, и 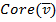 - ядро, которое (как уже было упомянуто ранее) определяется как множество вероятностей
- ядро, которое (как уже было упомянуто ранее) определяется как множество вероятностей 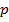 таких, что
таких, что 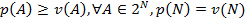 .
.
Авторы рассматривают только случай 2-чередующейся (субмодулярной) емкости (т. е. 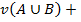
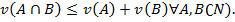
Расширение данного подхода было предложено Дюбуа Д. [12], где авторами представлен метод вычисления нижней границы без введения предположения о субмодулярности емкости и продемонстрировано его применение к многокритериальной задаче о кратчайшем пути в графе. Еще одно приложение интеграла Шоке в задачах комбинаторной оптимизации было представлено в работе [13]. Авторами решается задача программирования в ограничениях. Анализируемая проблема содержит три критерия, агрегация которых производится с помощью интеграла Шоке. Целью задачи является нахождение подмножества допустимого множества, на котором значение интеграла лежит в некотором заданном варианте:
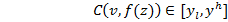
Интересен подход М.Тимонина к рассмотрению задачи максимизации интеграла Шоке без предположений о характере емкости и для произвольных вогнутых функций ценности, а также к задаче робастного программирования для случая, когда предпочтения лиц, принимающих решения, не позволяют однозначно определить выбор. [14]
Авторский метод поиска экстремальных значений интеграла Шоке и его применение в задачах принятия решений.
Фундаментальным вопросом теории экономики активного коннекта является задача построения корректного отображения бинарных отношений (т.н. «предпочтений») при выборе инновационных ресурсов предприятия на некотором абстрактном множестве объектов инноваций между элементами множества R. Математически данная задача может быть сформулирована как задача построения гомоморфизма между структурой, состоящей из абстрактного множества X и некоторого числа отношений на этом множестве, и структурой, состоящей из подмножества множества действительных чисел R, и привычных отношений, таких как «+» и др. Решение данной проблемы опирается на два основных класса теорем. Утверждения теорем представимости связывают определенные фундаментальные характеристики исходной структуры с принципиальной возможностью построения гомоморфизма. Утверждения теорем единственности описывают множество гомоморфизмов, связывающих характеризованную аксиомами структуру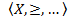 с одной и той же структурой
с одной и той же структурой 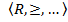 .
.
Важным классом задач принятия решений являются задачи принятия решений по сбалансированному распределению инновационных ресурсов между объектами инноваций в условиях неопределенности инновационной деятельности промышленных предприятий.
В ряде работ, опубликованных в 30–50 годах прошлого века, дается достаточно точный ответ на этот вопрос. Если предпочтения менеджеров предприятия, принимающих решения, согласуются с рядом фундаментальных свойств (аксиом), то возможно отображение этих предпочтений с помощью так называемой ожидаемой полезности (т. е. аддитивной модели).
Введем формальное определение задачи принятия решений в условиях неопределенности, которым будем называть «ансамбль» (S, X, F,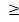 ), где S — множество состояний баланса инновационных ресурсов между объектами инноваций; X — множество исходов выбора объектов инноваций; F — множество действий функции из S на X;
), где S — множество состояний баланса инновационных ресурсов между объектами инноваций; X — множество исходов выбора объектов инноваций; F — множество действий функции из S на X;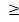 — отношение предпочтения на F.
— отношение предпочтения на F.
Таким образом, при условии, что предпочтения менеджеров, принимающих решения устранения диспаритетности баланса распределения инновационных ресурсов между объектами инноваций характеризуются «ансамблем», решение принимается так, как если бы существовало некоторое вероятностное распределение или субъективная вероятность, описывающее насколько возможно возникновение того или иного исхода, а наиболее предпочтительное решение при этом максимизирует ожидаемую полезность.
Вторым классом задач принятия решений данного характера являются многокритериальные задачи. Первым этапом является отбор объектов инноваций на основе Парето-оптимальности, то есть их поиск с недоминированными векторами оценок. Содержание данного этапа нами было рассмотрено в ранее опубликованных работах.
Многокритериальной задачей принятия решения будем называть «ансамбль» (N, X,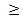 ), где N — множество критериев параметризации баланса распределения инновационных ресурсов предприятия между объектами инноваций;
), где N — множество критериев параметризации баланса распределения инновационных ресурсов предприятия между объектами инноваций;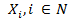 — множество значений критериев;
— множество значений критериев;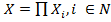 — множество «альтернатив» выбора объектов инноваций;
— множество «альтернатив» выбора объектов инноваций;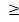 –отношение предпочтения выбора инновационных ресурсов на X.
–отношение предпочтения выбора инновационных ресурсов на X.
Теперь становится возможным привести теорему, характеризующую модель с аддитивной функцией ценности для случая не менее трех критериев:
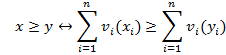 (1)
(1)
Частным случаем аддитивной модели является взвешенное арифметическое среднее:
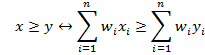 (2)
(2)
Неоспоримым преимуществом аддитивной модели является ее простота. В статье американского ученого Саваж Л. [15] впервые была предложена аксиоматизация принятия решений в условиях неопределенности, предпочтения, согласующиеся с упомянутыми аксиомами были названы рациональным поведением. Такая характеристика вызвала значительную критику, одним из наиболее известных примеров которой является так называемый парадокс Эллсберга Д. [16].
В многокритериальных задачах можно говорить о «взаимодействии» критериев: взаимодополнении, взаимозамещении, корреляции и т. д. В то же время, в задачах принятия решений в условиях неопределенности, нарушение аксиомы независимости могут появляться в задачах, характеризующихся недостаточной информацией, например, в случаях, когда возможное развитие событий описывается не одним, а несколькими возможными вероятностными распределениями.
Для разрешения проблем, связанных с интенциональными условиями аксиомы независимости, Шмейдлер Д. [17] предложил ослабить аксиоматику аддитивной модели, заменив независимость на так называемую комонотонную независимость, которая имеет следующий вид:
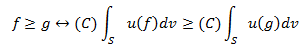 (3)
(3)
где 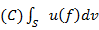 - интеграл Шоке, а дискретным интегралом Шоке является:
- интеграл Шоке, а дискретным интегралом Шоке является:
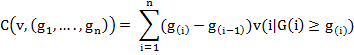 (4)
(4)
Данная модель является непосредственным обобщением аддитивной модели. С одной стороны, присутствие независимости подразумевает также и комонотонную независимость, а с другой — вероятность является частным случаем аддитивной емкости, а интеграл Шоке в данном случае совпадает с интегралом Лебега.
Результаты, полученные Шмейдлером Д., позволили получить средства для решения проблем, моделирование которых в рамках классических моделей было невозможным. Таким образом,был расширен сам язык моделирования задач принятия решений. В частности, неотображаемый в аддитивных моделях феномен «уклонения от неопределенности» возможно смоделировать с помощью интеграла Шоке.
Интеграл Шоке стал применяться также и в мнгокритериальных задачах принятия решений, а в последние годы получает все более широкое распространение. Также как и в случае с задачами принятия решений в условиях неопределенности, и даже в многокритериальных задачах интеграл Шоке позволил существенно расширить язык моделирования предпочтений менеджеров промышленных предприятий, принимающих решения по оптимизации распределения инновационных ресурсов между объектами инноваций.
Отсутствие аддитивности при моделировании процесса оптимизации распределения инновационных ресурсов между объектами инноваций несколько затрудняет анализ в интерпретации модели. Вместо «весов» критериев, т. е. значений меры на единичных элементах, в неаддитивном случае необходимо также учитывать все подмножества множества N, в которые входит интересующий нас критерий. Для проведения такого анализа, как правило, применяется широко известный в теории кооперативных игр вектор Шепли. Значения вектора Шепли лежат в интервале [0,1], а сумма всех значений равняется 1. Для анализа взаимодействия критериев индекс Шепли был обобщен на подмножества N произвольного размера и получил название индекса взаимодействия.
В таких условиях естественным критерием в многокритериальных задачах является Парето-доминирование: если некоторый элемент множества решений имеет значения по всем критериям не худшие, чем у некоторого другого элемента и превосходит его хотя бы по одному, то первый элемент является более предпочтительным. Аддитивные модели обеспечивают выполнение данного свойства. Однако, в неаддитивных моделях, учитывающих взаимодействие между критериями, может возникнуть ситуация, при которой два элемента будут иметь равную оценку, при том, что один из них Парето-доминирует.
В результате исследования выявлены несколько методов, позволяющих обеспечить соблюдение принципа Парето-доминирования при использовании интеграла Шоке:
- выбрать из множества оптимальных вариантов распределения инновационных ресурсов между объектами инноваций Парето-оптимальный. Поскольку 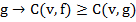 , то среди максимизаторов
, то среди максимизаторов 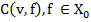 всегда найдется Парето-оптимальное решение.
всегда найдется Парето-оптимальное решение.
- установить Xₒ равным множеству Парето-оптимальных точек, то есть задача максимизации интеграла Шоке будет являться задачей уточнения решения среди Парето-оптимальных вариантов. Во многих прикладных задачах, такой переход может быть осуществлен сравнительно легко. Например, в задаче с ограничением распределения инновационных ресурсов предприятия между объектами инноваций 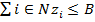 достаточно перейти к множеству
достаточно перейти к множеству 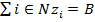 .
.
- уточнение емкости «ансамбля». Для случая, когда предпочтениям менеджеров предприятия удовлетворяет не одна, а несколько емкостей, предложены методы, которые позволяют уточнить емкость «ансамбля», с тем, чтобы Парето-доминирование соблюдалось как можно сильнее.
Выводы:
1. Независимость бинарных отношений инновационных ресурсов и объектов инноваций не выполняется в подавляющем большинстве практических задач по исследованию диспаритетности баланса распределения ресурсов. Ослабление данной аксиомы является необходимым условием для построения корректных моделей в задачах по принятию решений менеджерами предприятий для сбалансированного распределения инновационных ресурсов между объектами инноваций.
2. Интеграл Шоке позволяет отражать предпочтения менеджеров предприятий, нарушающие независимость «ансамбля» альтернатив их выбора. Его применение существенно расширяет возможности решений менеджеров, являющихся как многокритериальной задачей, так и задачей принятия решений в условиях неопределенности, позволяя моделировать, с одной стороны, разнообразные виды взаимодействия между критериями параметризации баланса распределения инновационных ресурсов, а с другой, ситуации принятия решений в условиях недостаточной информации для выбора объектов инноваций с целью оптимизации баланса распределения инновационных ресурсов.
3. На сегодняшний день методы поиска экстремальных значений интеграла Шоке и их применение в задачах принятия решений недостаточно исследованы, опубликованные работы обладают существенными ограничениями. Поэтому развитие данного направления исследования и создание более эффективных методик и алгоритмов на основе интеграла Шоке перспективно как в практическом, так и в теоретическом плане.
Литература:
1. Лавриченко О. В. Инновационные бизнесобразующие технологии как эндогенная основа инновационной системы промышленного предприятия: монография. — М.: Изд-во МосГУ «Социум»,2014.- 136 с.
2. Лавриченко О. В. Интенциональность научной концепции сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций // Молодой ученый.-2014.-№ 4(63).-С.565–570.
3. Lavrichenko O. V. Foundations of the theory of the economy of the active connect [Text]:materials of the IV International scientific conference on May 25–26,2014.-Prague, Sociosfera-CZ Publ.-P.44–54.
4. Лавриченко О. В. Разработка математического обеспечения системы управления инновационными ресурсами промышленных предприятий // Молодой ученый.-2014.-№ 8(67).-С.191–196.
5. Лавриченко О. В. Научная концепция сбалансированного распределения инновационных ресурсов промышленного предприятия между объектами инноваций // Научная перспектива.-2014.-№ 5(51).-С.89–92.
6. Lavrichenko O. V. Intentionality of the theory of economic of active connect // Paradigmata poznani. — Prague,Sociosfera-CZ.Publ. — 2014. — no.3.-P.22–28.
7. Лавриченко О. В. Оптимизация инновационной системы предприятий в условиях сбалансированного распределения инновационных ресурсов между объектами инноваций // Научный обозреватель.-2014.-№ 7(43).-С.52–56.
8. Лавриченко О. В. Учет влияния антропогенного фактора на управление инновационной системой промышленного предприятия // Научная перспектива.-2014.-№ 3(49).-С.116–119.
9. Лавриченко О. В. Оптимизация распределения инновационных ресурсов предприятий между объектами инноваций методом анализа неоднородных совокупностей // Журнал научных и прикладных исследований.-2014.-№ 7.-С.38–41.
10. Лавриченко О. В. Функция сходства многомерных объектов и отношение Парето в оперативном управлении распределением инновационных ресурсов промышленного предприятия // Молодой ученый.-2014.-№ 12(71).-С.87–90.
11. Galand L., Parny P., Spanjard O. A branch and bound algorihm for Choquet opnimization in multicriteria problems // Multiple criteria decision making for sustainable energy and transportation systems.-2010.-P.355–365.
12. Fouchal H.,Gandibleux X.,Le Huede F. Preferred solutions computed with alabal setting algorihm based on Choquet integral for multi-objective shortest paths // Simposium on computational intelligence in multicriteria decision-making.-2011.-P.76–78.
13. Le Huede F.,Grabish M.,Labrenche C.,Saveaut P. MCS — a new algorihm for multicriteria optimization in constant programming // Annals of operational research.-2006.-Vol.147.-P.143–174.
14. Timonin M. Robust optimization of the Choque integral. [Электронный ресурс].URL:htpp://www.sciencedirect.com/science/article/pii/SO165011412001856 (дата обращения: 14.06.2014).
15. Savage L. J. The theory of statistical decision // Journal of the American statistical association.-1951.-Vol.46.-no.253.-P.55–67.
16. Ellsberg D. Risk,ambiguity and the Savage axioms // The Quarterly journal of economics.-1961.-Vol.75.-no.4.-P.643–669.
17. Dubois D., Fargier H. Capacity refinements and their application to qualitative decision avaluation. [Электронный ресурс]. URL:http://www.dx.doi.org/10.1007/978–3-642–02906–6_28 (дата обращения:14.06.2014).
Ключевые слова
инновационные самоорганизующиеся бизнесобразующие технологии, инновационные ресурсы, антропогенные факторы, , экономика активного коннекта, антропогенные сукцессии, интеграл ШокеПохожие статьи
Декомпозиция задачи оптимизации сбалансированного...
Ключевые слова: инновационные ресурсы промышленного предприятия, инновации
Кроме того, распределение инновационных ресурсов промышленного предприятия в
Литература: 1. Лавриченко О. В. Инновационные бизнесобразующие технологии как...
Инновационные технологии в современном учебном процессе.
самоорганизующаяся бизнесобразующая технологий, инновационная бизнесобразующая технологии, инновационная стратегия развития, промышленное предприятие... Ключевые слова: инновационные ресурсы промышленного...
Использование методов принятия решений в условиях...
Примерами задач принятия решения в условиях неопределённости могут служить: выбор направления развития предприятия, выбор варианта производимого товара, выбор банка для вклада или кредита, выбор проекта электростанции.
Интенциональность научной концепции сбалансированного...
...инновационная бизнесобразующая технологии, инновационная стратегия развития, промышленное предприятие, самоорганизующаяся бизнесобразующая технологии, инновационная бизнесобразующая технологий, инновационное развитие...
инновация, инновационная система предприятия, ресурс...
1. Лавриченко О. В. Инновационные бизнесобразующие технологии как эндогенная основа инновационной системы промышленного
инновация, инновационная система предприятия, сбалансированное распределение, ресурс, предприятие, инновационный...
Основные принципы и задачи инновационной деятельности...
Ключевыми задачами организации инновационной деятельности любого предприятия
В условиях рыночной экономики инновационная деятельность должна способствовать
Инновационная деятельность организации должна быть сосредоточена на решении главных...
инновация, инновационная система предприятия, ресурс...
Основные термины (генерируются автоматически): инновация, ресурс, сбалансированное распределение, инновационная система предприятия
В статье рассматривается концепция инновационных самоорганизующихся бизнесобразующих технологий, определены их...
инновации, инновационные ресурсы, научная концепция...
...инновация, инновационная система предприятия, сбалансированное распределение, ресурс, предприятие, инновационный ресурс
В статье рассматривается концепция инновационных самоорганизующихся бизнесобразующих технологий, определены их...
Почему именно инновационные бизнесобразующие технологии?
...необходимо сбалансированное (оптимальное) распределение инновационных ресурсов промышленных предприятий между объектами инноваций на основе инновационных самоорганизующихся бизнесобразующих технологий.
Похожие статьи
Декомпозиция задачи оптимизации сбалансированного...
Ключевые слова: инновационные ресурсы промышленного предприятия, инновации
Кроме того, распределение инновационных ресурсов промышленного предприятия в
Литература: 1. Лавриченко О. В. Инновационные бизнесобразующие технологии как...
Инновационные технологии в современном учебном процессе.
самоорганизующаяся бизнесобразующая технологий, инновационная бизнесобразующая технологии, инновационная стратегия развития, промышленное предприятие... Ключевые слова: инновационные ресурсы промышленного...
Использование методов принятия решений в условиях...
Примерами задач принятия решения в условиях неопределённости могут служить: выбор направления развития предприятия, выбор варианта производимого товара, выбор банка для вклада или кредита, выбор проекта электростанции.
Интенциональность научной концепции сбалансированного...
...инновационная бизнесобразующая технологии, инновационная стратегия развития, промышленное предприятие, самоорганизующаяся бизнесобразующая технологии, инновационная бизнесобразующая технологий, инновационное развитие...
инновация, инновационная система предприятия, ресурс...
1. Лавриченко О. В. Инновационные бизнесобразующие технологии как эндогенная основа инновационной системы промышленного
инновация, инновационная система предприятия, сбалансированное распределение, ресурс, предприятие, инновационный...
Основные принципы и задачи инновационной деятельности...
Ключевыми задачами организации инновационной деятельности любого предприятия
В условиях рыночной экономики инновационная деятельность должна способствовать
Инновационная деятельность организации должна быть сосредоточена на решении главных...
инновация, инновационная система предприятия, ресурс...
Основные термины (генерируются автоматически): инновация, ресурс, сбалансированное распределение, инновационная система предприятия
В статье рассматривается концепция инновационных самоорганизующихся бизнесобразующих технологий, определены их...
инновации, инновационные ресурсы, научная концепция...
...инновация, инновационная система предприятия, сбалансированное распределение, ресурс, предприятие, инновационный ресурс
В статье рассматривается концепция инновационных самоорганизующихся бизнесобразующих технологий, определены их...
Почему именно инновационные бизнесобразующие технологии?
...необходимо сбалансированное (оптимальное) распределение инновационных ресурсов промышленных предприятий между объектами инноваций на основе инновационных самоорганизующихся бизнесобразующих технологий.











