Анализ надежности Центра системы управления движением судов на примере порта Новороссийск
Автор: Тюфанова Анастасия Александровна
Рубрика: 9. Транспорт
Опубликовано в
Дата публикации: 17.07.2014
Статья просмотрена: 166 раз
Библиографическое описание:
Тюфанова, А. А. Анализ надежности Центра системы управления движением судов на примере порта Новороссийск / А. А. Тюфанова. — Текст : непосредственный // Современные тенденции технических наук : материалы III Междунар. науч. конф. (г. Казань, октябрь 2014 г.). — Т. 0. — Казань : Бук, 2014. — С. 69-76. — URL: https://moluch.ru/conf/tech/archive/123/6052/ (дата обращения: 20.04.2024).
В статье рассмотрен процесс функционирования системы управления движением судов. Для анализа надежности Центра системы управления движением судов использована математическая модель многоканальной системы массового обслуживания с отказами. В результате сделан вывод о том, что работу Центра системы управления движением судов можно рассматривать как диспетчерский пункт.
Ключевые слова: надежность, система управления движением судов, многоканальная система массового обслуживания, безотказная работа.
In clause process of functioning of Vessels Traffic Service (VTS) is considered. It is drawn a conclusion that at the analysis of reliability Center of Vessels Traffic Service its work can be considered as a control office consisting of operator VTS and the local computer network, including: the central computer, the equipment of data input in the central computer, switchboards and display units. The analysis of reliability of the Center Vessels Traffic Service with use as mathematical model of multichannel system of mass service with refusals is lead.
Keywords: reliability, Vessels Traffic Service, multichannel system of mass service, non-failure operation.
Для организации повседневной деятельности, эксплуатации технических средств, а также для размещения оборудования и персонала в составе системы управления движением судов (СУДС) созданы Центр СУДС (ЦСУДС) и информационные радиотехнические посты (РТП). РТП обеспечивают ЦСУДС информацией о навигационной обстановке в районе действия системы. ЦСУДС осуществляет обработка, хранение информации, взаимодействие СУДС с судами и организует деятельность операторов СУДС. Непрерывная круглосуточная деятельность системы обеспечивается сменно-вахтенной работой персонала. Каждую смену возглавляет начальник смены, руководящий деятельностью операторов СУДС, инженерно-технического и вспомогательного персонала, входящих в состав смены [1, с. 12].
В процессе функционирования СУДС береговые радиолокационные станции просматривают пространство в районе действия и обнаруживают суда, находящиеся в ней. Отраженные от судов радиолокационные сигналы расшифровываются, очищаются от помех и проходят предварительную обработку в аппаратуре съема данных. Далее эти данные преобразуются в такую форму, в которой они могут быть введены в вычислительное устройство (радар-процессор). Вычислительное устройство проводит обработки радиолокационной информации — первичную (определение координат точек локации) и вторичную (построение трасс движения судов) [2, с. 45].
При помощи средств голосовой ОВЧ связи с судном устанавливается двусторонняя связь. Сведения, поступающие с борта судов, позволяют выделить суда, направляющиеся в данный порт, и отсеять суда, следующие в другие порты. Дальнейшей обработке подвергается информация лишь о тех судах, которые направляются в данный порт. После дополнительной обработки эта информация через аппаратуру ввода данных передается в ЦСУДС. Связь с судами, следующими в другие порты, поддерживается только для передачи им метеорологических и гидрологических данных, сведений о радиомаяках и т. д.
Таким образом, центральное вычислительное устройство ЦСУДС поступает радиолокационная информация обо всех судах находящихся в районе действия. Центральное вычислительное устройство выполняет дополнительную обработку этой информации (интегрирование с данными автоматической идентификационной системы). Здесь решается задача анализа собранных данных и определения порядка обслуживания судов. В первую очередь определяется маршрут следования каждого судна, выделяется соответствующее место якорной стоянки и начинается радиолокационный контроль проводки судна. В этом случае СУДС может осуществлять несколько функций:
1) контроль за движением судна, при которой ЦСУДС передает на контролируемые суда информацию, предупреждения о развитии опасных ситуаций, а также рекомендации по их предотвращению;
2) помощь в судовождении, оказываемая по запросу судна или по решению ЦСУДС, преимущественно в сложных гидрометеорологических условиях, при выходе из строя или отсутствии на судне приборов, обеспечивающих безопасное движение судна, путем регулярной передачи Центром следующей информации: позиции судна по отношению к навигационному ориентиру, фарватеру и путевым точкам; путевого угла и путевой скорости судна; положений и намерений других судов; рекомендации по изменению курса и скорости [1, с. 16].
Следовательно, при анализе надежности ЦСУДС его работу можно рассматривать как диспетчерский пункт, состоящий из оператора СУДС и локальной вычислительной сети, включающей в себя: центральное вычислительное устройство, аппаратуру ввода данных в центральное вычислительное устройство, коммутаторы и устройства отображения информации. ЦСУДС представляет собой обслуживающий орган, предназначенный для оперирования над интенсивными потоками информации и структура которого приспособлена к выполнению специальных мероприятий, направленных на оптимальный сбор, хранение, переработку и выдачу больших массивов информации. Поток заявок ЦСУДС — суда, прибывающие в порт. Оператор может обслуживать несколько судов одновременно. Промежутки времени между заходами судов являются случайными. Возможен случай отказа ЦСУДС в заходе судна в порт с отправлением его в зону ожидания (на рейд). Это объясняется единственной причиной — гидрометеорологическими условиями («бора» и южный ветер). Поэтому ЦСУДС представляет собой многоканальную систему массового обслуживания (СМО) с отказами. Предположим, что интенсивность потока судов в районе действия СУДС Новороссийск есть величина постоянная и равная 2 судна в час, т. е. λ=2 час-1, интенсивность обслуживания судна диспетчером равна μ= 4 час-1. Так как интенсивность обслуживания μ>λ, то обслуживание судов было бы абсолютно надежным, если не существовала бы причина для отказа в принятии судна. Определим показатели надежности ЦСУДС: вероятность безотказной работы (PС(t)); среднее время безотказной работы (Т1); функцию готовности (КГ(t)); коэффициент готовности (КГ); наработку на отказ (Т) — в условиях случайности потока судов
Аналогом функционирования многоканальной СМО с отказами является восстанавливаемая система с резервированием по методу замещения с кратностью, равной числу n одновременно обслуживаемых заявок (рисунок 1, А) и Б)).
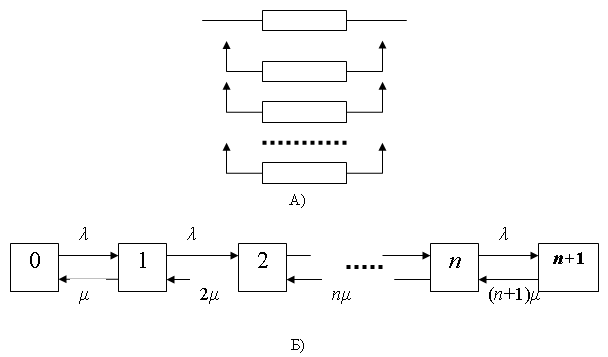
Рис. 1. Структурная схема (А) и граф состояний (Б) системы. λ — интенсивность отказов нерезервированной системы; μ — интенсивность восстановления; n — кратность резервирования, равная числу резервных элементов
Математическая модель функционирования СМО с отказами представим системой дифференциальных уравнений:
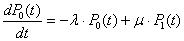 ;
;
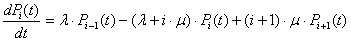 , i =1, 2, …, n-2; (1)
, i =1, 2, …, n-2; (1)
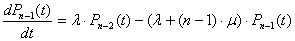 ;
;
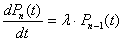 ,
,
где Р0(t) — вероятность того, что в момент t система находится в состоянии обслуживания заявок; Pi(t), i=1,2,…, n-1 — вероятность того, что в момент времениt система находится в состоянии обслуживания i заявок; Pn(t) — вероятность того, что в момент t система находится в отказовом состоянии, т. е. на обслуживании находится предельное число заявок и очередной заявке будет отказано в обслуживании.Pn(t) является вероятностью отказа системы в течение времени t.
Тогда вероятность безотказной работы системы PC(t) выражается зависимостью: PC(t)=1 — Pn(t) (2)
Получим математическую модель системы из состояния Sn в исправное состояние Sn+1,
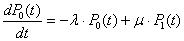 ;
;
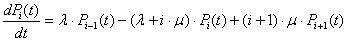 , i=1, 2, …, n-1; (3)
, i=1, 2, …, n-1; (3)
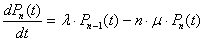 .
.
Вероятность Pn(t) имеет смысл неготовности системы принять очередную заявку в момент времени t (коэффициент простоя) [3, с. 23]. Тогда функцией готовности КГ(t) имеет следующее выражение:
КГ(t)=1 — Pn(t). (4)
При 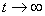 вероятности P0, Pi, Pn, стремятся к постоянным величинам, и система дифференциальных уравнений (3) превращается в систему алгебраических уравнений, которая имеет бесчисленное множество решений:
вероятности P0, Pi, Pn, стремятся к постоянным величинам, и система дифференциальных уравнений (3) превращается в систему алгебраических уравнений, которая имеет бесчисленное множество решений:
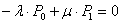 ;
;
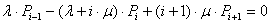 , i=1, 2, …, n-1; (5)
, i=1, 2, …, n-1; (5)
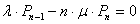 .
.
Однако существует уравнение P0+ P1+…+ Pn=1, которое замещает одно любое уравнение системы (5), при этом она имеет единственное решение. В (5) вероятность Pn — коэффициент неготовности системы, поэтому коэффициент готовности, как предельное значение функции готовности, определяется выражением:
КГ =1 — Pn. (6)
Вычисление вероятности безотказной работы ЦСУДС требует решения системы дифференциальных уравнений (1), для чего используем следующий метод:
- система (1) записывается в виде преобразования Лапласа;
- система алгебраических уравнений в преобразованиях Лапласа решается с помощью универсальных математических программных средств символьной математики (Mathematica, Maple, Derive, Mathcad, Mathlab) [4–5, с. 3, с. 12];
- находится обратное преобразование Лапласа с помощью тех же систем символьной математики;
- по вероятности безотказной работы находится среднее время безотказной работы, используя соотношение: 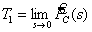 .
.
Система (1) в преобразовании Лапласа имеет вид:
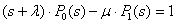 ;
;
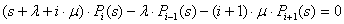 , i=1, 2, …, n-1; (7)
, i=1, 2, …, n-1; (7)
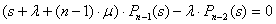 ;
;
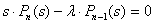 .
.
Предположим, что начальными условиями являются P0(0)=1, P1(0)= =P2(0)=…=Pn(0)=0. Решение этой системы уравнений выполнено с помощью математической программы Derive 5, результаты вычисления вероятности отказа Pn(s) приведены в диапазоне n от 1 до 7:
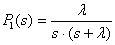 ;
;
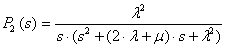 ;
;
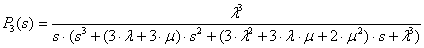 ;
;
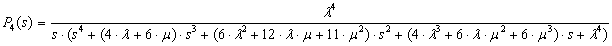 ;
;
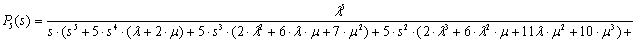
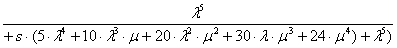 ;
;
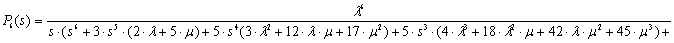
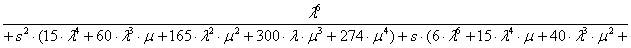
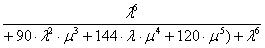 ;
;
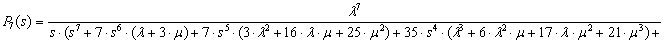
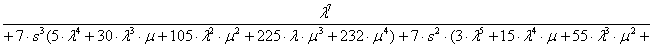
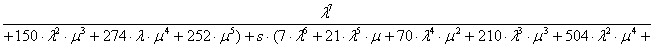
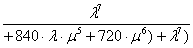 .
.
Формулы для вероятностей отказа в течение времени t получены в результате вычисления оригиналов функций Pn(s). Обратное преобразование Лапласа выполнено с помощью математической программы Mathematica, которая позволяет получить аналитические выражения при n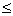 4. Далее приведены оригиналы функций P1(t) и P2(t) в символьном виде:
4. Далее приведены оригиналы функций P1(t) и P2(t) в символьном виде:
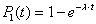 ,
,
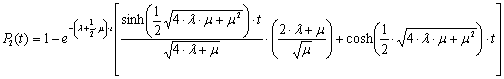 .
.
Расчетные соотношения при n>2 для ЦСУДС, когда значения λ =2, μ=4 имеют вид:
n=1, 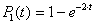 ;
;
n=2, 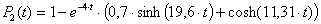 ;
;
n=3, 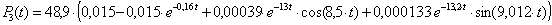 ;
;
n=4, 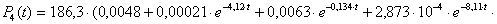
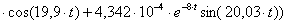 ;
;
n=5, 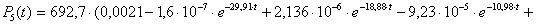
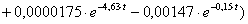 ;
;
n=6, 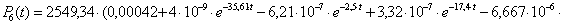
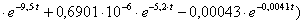 ;
;
n=7, 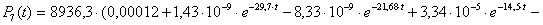
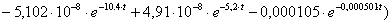 ;
;
В таблицах 1–3 приведены значения вероятностей отказа ЦСУДС при n=2 и n=7 в широком диапазоне времени работы системы от 1 до 10000 час.
Таблица 1
Значения вероятности отказа P2(t)
|
t, час |
P2(t) |
|
|
γ=1,25 |
γ=2 |
|
|
1 |
0,6987 |
0,7841 |
|
2 |
0,9194 |
0,9453 |
|
3 |
0,9479 |
0,9682 |
|
4 |
0,9921 |
0,9945 |
|
5 |
0,9978 |
0,9989 |
|
6 |
0,9991 |
0,9996 |
|
7 |
0,9994 |
0,9998 |
|
8 |
0,9998 |
0,9999 |
|
9 |
0,99993 |
0,99996 |
|
10 |
0,99995 |
0,99997 |
Таблица 2
Значения вероятности отказа P7(t)
|
t, час |
P7(t) |
|
|
γ=1,25 |
γ=2 |
|
|
0 |
0,021016 |
0,0560145 |
|
100 |
0,043431 |
0,9923401 |
|
200 |
0,088111 |
0,1560817 |
|
300 |
0,130697 |
0,2135687 |
|
400 |
0,171287 |
0,2965432 |
|
500 |
0,209975 |
0,3695104 |
|
600 |
0,245068 |
0,3952387 |
|
700 |
0,289719 |
0,4123256 |
|
800 |
0,315694 |
0,4598011 |
|
900 |
0,342674 |
0,5498756 |
|
1000 |
0,375987 |
0,5696363 |
Таблица 3
Значения вероятности отказа P7(t) (в другом диапазоне)
|
t, час |
P7(t) |
|
|
γ=1,25 |
γ=2 |
|
|
0 |
0,021016 |
0,123785 |
|
1000 |
0,377859 |
0,453622 |
|
2000 |
0,613804 |
0,897211 |
|
3000 |
0,759802 |
0,905583 |
|
4000 |
0,850144 |
0,953221 |
|
5000 |
0,906046 |
0,981232 |
|
6000 |
0,940637 |
0,988856 |
|
7000 |
0,962042 |
0,995102 |
|
8000 |
0,975286 |
0,998735 |
|
9000 |
0,983482 |
0,999101 |
|
104 |
0,988553 |
0,9994534 |
Из таблиц 1–3 следует, что вероятность безотказной работы существенно зависит от времени t, числа заявок n, одновременно обслуживаемых оператором СУДС, интенсивностей потока заявок λ и обслуживания μ. С увеличением времени безотказной работы системы и интенсивности потока требований вероятность безотказной работы убывает. Вероятность отказа в обслуживании зависит от числа заявок n, одновременно обслуживаемых оператором СУДС. При больших значениях n вероятность отказа в обслуживании слабо зависит от интенсивности λ.
Для получения формулы среднего времени безотказной работы используем выражения для вероятностей безотказной работы в преобразовании Лапласа. Преобразование Лапласа вероятности безотказной работы системы равно: 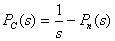 .
.
Для вычисления среднего времени безотказной работы воспользуемся предельным соотношением:
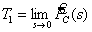 [3, с.34]. (8)
[3, с.34]. (8)
В результате вычислений с помощью Mathematica получены выражения:
n=1, 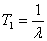 ;
;
n=2, 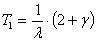 ;
;
n=3, 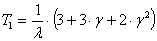 ;
;
n=4, 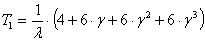 ;
;
n=5, 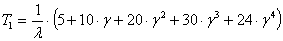 ;
;
n=6, 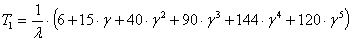 ;
;
n=7, 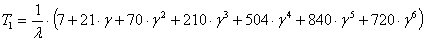 , где
, где 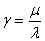 ,
,
которые позволяют получить общую формулу для среднего времени безотказной работы:
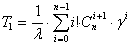 . (9)
. (9)
В таблице 4 приведены значения среднего времени безотказной работы при n=1, 2, …, 7 и при следующих значениях γ: 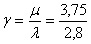 =1,25;
=1,25; 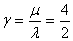 =2.
=2.
Таблица 4
Значения среднего времени безотказной работы
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
T1, час, γ=1,25 |
0,48 |
1,625 |
4.938 |
16,297 |
82,969 |
490,402 |
35470 |
|
T1, час, γ=2 |
0,5 |
2 |
8,5 |
44 |
364,5 |
355000 |
41520000 |
Из таблицы 4 видно, что среднее время безотказной работы существенно возрастает с увеличением числа операторов СУДС.
ЦСУДС является системой длительной работы, поэтому необходимо оценивать его готовность коэффициентом готовности (КГ). Критерии готовности системы во многом определяют показатели эффективности системы, риск, безопасность. Систему дифференциальных уравнений (3) решим, при начальных условиях: P0(0)=1, Pi(0)=0, i=1, 2, …, n, которая в преобразовании Лапласа будет иметь вид:
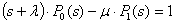 ;
;
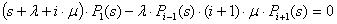 ,i=1, 2, …, n-1; (10)
,i=1, 2, …, n-1; (10)
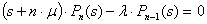 .
.
Относительно неизвестных P0(s), P1(s), …, Pn(s) (10) является системой линейных алгебраических уравнений с постоянным коэффициентами. Главный ее определитель М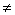 0, поэтому она имеет единственное решение, которое получено с помощью Derive 5. Полученные результаты решения системы уравнений для случаев n=1, 2, 3:
0, поэтому она имеет единственное решение, которое получено с помощью Derive 5. Полученные результаты решения системы уравнений для случаев n=1, 2, 3:
n=1: 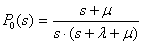 ,
, 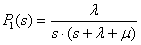 ;
;
n=2: 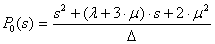 ,
, 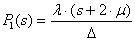 ,
, 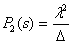 ,
,
где 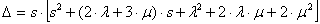 ;
;
n=3: 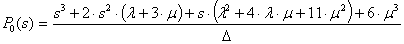 ,
,
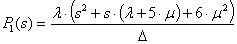 ,
, 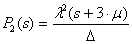 ,
, 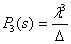 ,
,
где 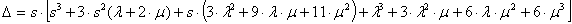 .
.
Для получения аналитических выражений вероятностей состояний во временной области находим обратные преобразования Лапласа, приведенных ранее решений. Решение получено с помощью Mathcad 2006. При n=1, 2 значения вероятностей имеют вид:
n=1: 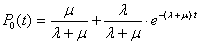 ,
, 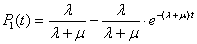 ;
;
n=2: 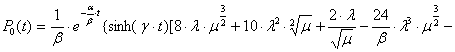
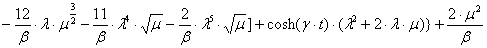 ,
,
где 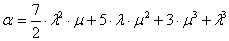 ;
; 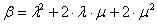 ;
; 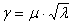 .
.
Подставляя числовые значения λ и μ, получим:
1) λ = 2,8 час-1, μ=3,75 час-1.
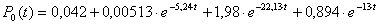 ;
;
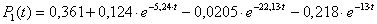 ;
;
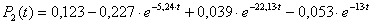 ;
;
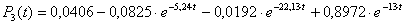 .
.
2) λ = 2 час-1, μ = 4 час-1.
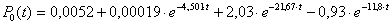 ;
;
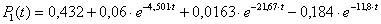 ;
;
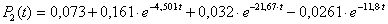 ;
;
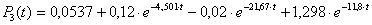 .
.
Воспользовавшись выражением КГ =1–Pn, определим коэффициент готовности. Значение Pn, полученное из графа состояний на рисунке 1, Б), имеет вид:
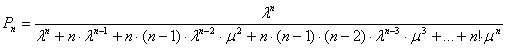 .
.
Разделив числитель и знаменатель на 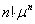 , получим следующую формулу:
, получим следующую формулу:
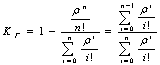 . (11)
. (11)
Подставляя значение 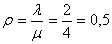 в формулу (11), получим значения коэффициента готовности (таблица 5).
в формулу (11), получим значения коэффициента готовности (таблица 5).
Таблица 5
Значения коэффициента готовности ЦСУДС
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
KГ |
0,86 |
0,97 |
0,998 |
0,999 |
0,9997 |
0,9998 |
0,99991 |
Из таблицы 5 видно, что коэффициент готовности существенно зависит от числа судов, одновременно обслуживаемых оператором СУДС.
Наработка на отказ рассчитывается по формуле: 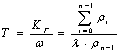 , поскольку
, поскольку 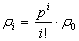 , то
, то 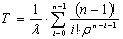 , или окончательно:
, или окончательно:
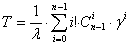 , (12)
, (12)
где 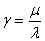 .
.
Подставляя в выражение (12) значение γ=2, получим значение наработки на отказ в зависимости от n. Значения наработки на отказ приведены в таблице 6.
Таблица 6
Значения наработки на отказ ЦСУДС
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Т, час |
0,65 |
0,87 |
2,94 |
8,83 |
41 |
338 |
2756 |
Из анализа надежности ЦСУДС порта Новороссийск, как диспетчерского пункта, можно сделать следующие выводы:
- вероятность безотказной работы существенно зависит от времени t, числа заявок n, одновременно обслуживаемых оператором СУДС, интенсивностей потока заявок λ и обслуживания μ;
- с увеличением времени безотказной работы системы и интенсивности потока требований вероятность безотказной работы убывает;
- вероятность отказа в обслуживании зависит от числа заявок n, одновременно обслуживаемых оператором СУДС.
Литература:
1. Положение о системах управления движением судов. М., 2002.
2. Бусленко, Н. П. Моделирование сложных систем// М.: Наука, 1978. — С. 400.
3. Половко, А. М. Основы теории надежности/А. М. Половко, С. В. Гуров//Спб.: БХВ-Петербург, 2006. — С. 704.
4. Половко, А. М. Derive 5для студентов// Спб.: БХВ-Петербург, 2005. — С.138.
5. Манзон, Б. М. Maple 5 Power Edition// М.: Филин, 1998. — С. 210.
6. Дьяков, В. П. Mathcad 8/2000 Специальный справочник//Спб.: Питер, 2000. — С. 367.
7. Дьяков, В. П. Системы символьной математики. Mathematica 2 и Mathematica 3// М.: СК Пресс, 1998. — С. 249.
Ключевые слова
надежность, система управления движением судов, многоканальная система массового обслуживания, безотказная работаПохожие статьи
безотказная работа, движение судов, вероятность, система...
Анализ надежности Центра системы управления движением... безотказная работа, движение судов, вероятность, система, центральное вычислительное устройство, коэффициент готовности, VTS, вероятность отказа, безотказная работа системы, число заявок.
Факторы, влияющие на эксплуатационную надежность технических...
- Характеристика безотказности — распределение времени безотказной работы системы. Рассмотрим процесс функционирования СУДС в реальных условиях, при которых неизбежны отказы ее технических средств.
Расчет надежности железобетонных элементов конструкций
Найдем вероятность безотказной работы по формуле (7), подставив полученное значение из (9): Далее рассмотрим прочностные свойства арматуры. Расчет вероятности отказа ибезотказной работы элемента по прочности арматуры на растяжение.
Ключевые слова:гидротехника, вероятность безотказной работы...
Противоположностью вероятности безотказной работы является вероятность отказов
Среднее время безотказной работы. где N0 — число узлов объекта до первого отказа для заданной партии.
Методы повышения уровня надежности систем АСУЗ
‒ — вероятность безотказного выполнения системой i-ой функции (вероятность безотказной работы i-ой функции АСУЗ) в течение заданного времени . Комплексными показателям безотказности и ремонтопригодности...
Вероятности безотказной работы элементов структурной схемы...
Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов определяет безотказность объекта. Показатель вероятности безотказной работы определяется статистической оценкой
Математическая модель анализа эксплуатационной надежности...
Действующие системы управления движением судов (СУДС) являются восстанавливаемыми, резервированными, дублированными, частично обслуживаемыми
Коэффициент готовности является комплексным показателем надежности, который характеризует безотказность и...
Роль ускоренных испытаний в определении надежности...
Анализ надежности Центра системы управления движением судов...
Наиболее высокая интенсивность отказов работы клапанов — регуляторов наблюдается на линиях сброса воды из первичных сепараторов...
Объект как система массового обслуживания: моделирование...
Определим время безотказной работы системы (режущий инструмент, покрышка колеса автомобиля и т. д.), а затем и поток отказов системы в этоминтервале. Если инструмент может получить повреждение с вероятностью , то вероятность того...
Похожие статьи
безотказная работа, движение судов, вероятность, система...
Анализ надежности Центра системы управления движением... безотказная работа, движение судов, вероятность, система, центральное вычислительное устройство, коэффициент готовности, VTS, вероятность отказа, безотказная работа системы, число заявок.
Факторы, влияющие на эксплуатационную надежность технических...
- Характеристика безотказности — распределение времени безотказной работы системы. Рассмотрим процесс функционирования СУДС в реальных условиях, при которых неизбежны отказы ее технических средств.
Расчет надежности железобетонных элементов конструкций
Найдем вероятность безотказной работы по формуле (7), подставив полученное значение из (9): Далее рассмотрим прочностные свойства арматуры. Расчет вероятности отказа ибезотказной работы элемента по прочности арматуры на растяжение.
Ключевые слова:гидротехника, вероятность безотказной работы...
Противоположностью вероятности безотказной работы является вероятность отказов
Среднее время безотказной работы. где N0 — число узлов объекта до первого отказа для заданной партии.
Методы повышения уровня надежности систем АСУЗ
‒ — вероятность безотказного выполнения системой i-ой функции (вероятность безотказной работы i-ой функции АСУЗ) в течение заданного времени . Комплексными показателям безотказности и ремонтопригодности...
Вероятности безотказной работы элементов структурной схемы...
Вероятность безотказной работы обратна вероятности отказа и вместе с интенсивностью отказов определяет безотказность объекта. Показатель вероятности безотказной работы определяется статистической оценкой
Математическая модель анализа эксплуатационной надежности...
Действующие системы управления движением судов (СУДС) являются восстанавливаемыми, резервированными, дублированными, частично обслуживаемыми
Коэффициент готовности является комплексным показателем надежности, который характеризует безотказность и...
Роль ускоренных испытаний в определении надежности...
Анализ надежности Центра системы управления движением судов...
Наиболее высокая интенсивность отказов работы клапанов — регуляторов наблюдается на линиях сброса воды из первичных сепараторов...
Объект как система массового обслуживания: моделирование...
Определим время безотказной работы системы (режущий инструмент, покрышка колеса автомобиля и т. д.), а затем и поток отказов системы в этоминтервале. Если инструмент может получить повреждение с вероятностью , то вероятность того...











