Использование анализа размерностей в геометрии
Авторы: Неграш Александр Сергеевич, Мазейкина Мара Юрьевна
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
международная научная конференция «Педагогическое мастерство» (Москва, апрель 2012)
Статья просмотрена: 1038 раз
Библиографическое описание:
Неграш, А. С. Использование анализа размерностей в геометрии / А. С. Неграш, М. Ю. Мазейкина. — Текст : непосредственный // Педагогическое мастерство : материалы I Междунар. науч. конф. (г. Москва, апрель 2012 г.). — Москва : Буки-Веди, 2012. — С. 165-169. — URL: https://moluch.ru/conf/ped/archive/22/1991/ (дата обращения: 25.04.2024).
Анализ размерностей физических величин и связанная с ним теория подобия физических явлений широко используются во многих технических приложениях физики. В то же время использованию этого анализа в школе не уделяется достаточного внимания при обучении физике.
Одной из причин этого является недостаточное количество учебных пособий для школы [1, 2, 3], где этот анализ представлен. Однако возможности использования этого анализа в школах имеются[4].
В данной работе представлены примеры использования анализа размерностей в геометрии, которые можно использовать на уроках физики как иллюстрацию возможностей такого анализа.
Подобие геометрических объектов это частный случай подобия физических объектов.
К удовлетворению учителей физики – сторонников использования активных форм анализа размерностейв школе – в учебниках геометрии сформулирована следующая теорема подобия геометрических фигур.
Теорема 1.Отношение площадей подобных фигур равно квадрату отношения их сходственных размеров.
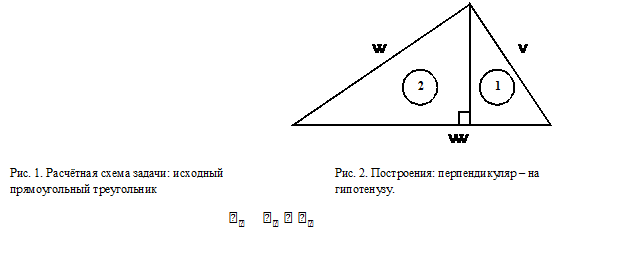
Такими сходственными размерами могут служить размеры, принятые за «характерные размеры». За характерные размеры можно принять, например, максимальные расстояния между точками подобных фигур.Для прямоугольных треугольников это будут их гипотенузы.
Докажем теорему Пифагора (теорему 2), применяя анализ размерностей, используемый в физике [3].
ТЕОРЕМА ПИФАГОРА
Задача № 1. Теорема 2 (теорема Пифагора)
Постановка задачи
Установить функциональную
зависимость между катетами
![]() прямоугольного
треугольника и гипотенузой
прямоугольного
треугольника и гипотенузой
![]() .
.
Исходные данные
Данный треугольник (![]() – прямоугольный – см. рис. 1.
– прямоугольный – см. рис. 1.
Вопрос задачи:
найти функциональную связь между сторонами
![]()
Обозначения
![]() – длины сторон
данного треугольника –
– длины сторон
данного треугольника –
![]() ,
,
![]() –
символ геометрического
подобия,
–
символ геометрического
подобия,
ИФ – итоговая формула.
Решение (доказательство)
Опустим
перпендикуляр из вершины прямого угла данного треугольника (![]() на гипотенузу
на гипотенузу![]() – см. рис. 2.
– см. рис. 2.
В результате![]() разбит на два прямоугольных треугольника: треугольник № 1 (
разбит на два прямоугольных треугольника: треугольник № 1 (![]() и треугольник №2 (
и треугольник №2 (![]() с гипотенузами
с гипотенузами
![]() ,
т. е.
,
т. е.
Треугольники
1 и 2 (![]() и
и
![]() )
подобны треугольнику 3 (
)
подобны треугольнику 3 (![]() ),
т. к. каждый из треугольников (1 и 2) имеет по одному общему острому
углу с данным треугольником
),
т. к. каждый из треугольников (1 и 2) имеет по одному общему острому
углу с данным треугольником
![]() ,
т. е.
,
т. е.
Т. о., все три треугольника подобны.
Выразим площадь каждого из треугольников через свой характерный размер – гипотенузу.
На основании анализа размерностей (чтобы сохранить равенство размерностей в формулах) длину гипотенузы необходимо возвести в квадрат.
Т. е.
|
. (ИФ3) |
-
Теорема 3 (теорема Пифагора)
В прямоугольном треугольнике квадрат гипотенузы равенсумме квадратов катетов.(3)
Теорема доказана (задача решена).
2.АНАЛИЗ РЕШЕНИЯ ЗАДАЧИ. ДОПОЛНИТЕЛЬНЫЕ ФОРМУЛИРОВКИ
ТЕОРЕМЫ ПИФАГОРА
Аналитическое выражение (ИФ3) теоремы графически можно представить другой расчётной схемой – квадратами, построенными на сторонах исходного прямоугольного треугольника и формулой (ИФ1) – см. рис. 3. Заметим, что все квадраты подобны друг другу.
Тогда вербальная формулировка аналитической формы (ИФ3) теоремы Пифагора примет вид теоремы 3.1.
|
Теорема 3.1 (теорема Пифагора – формулировка на языке площадей квадратов) |
|
Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе. (3.1) |
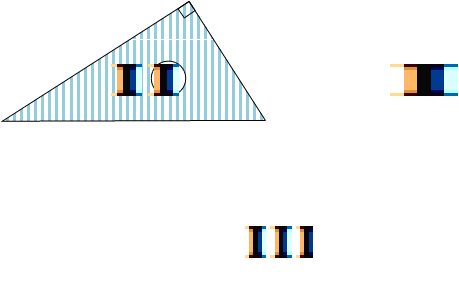
Если каждый из трёх прямоугольных треугольников, изображённых на рис. 2, отразить от своей гипотенузы как от плоского зеркала, то эти отражения, будут представлять собой прямоугольные треугольники, построенные на сторонах исходного прямоугольного треугольника – см. рис. 4. Тогда вербальная формулировка формулы (ИФ1) примет вид теоремы 3.2.
|
Теорема 3.2 (теорема Пифагора – формулировка на языке площадей прямоугольных треугольников) |
|
Сумма площадей подобных прямоугольных треугольников, построенных на катетах прямоугольного треугольника, равна площади подобного им прямоугольного треугольника, построенного на гипотенузе. (3.2) |
Анализируя рисунки 3, 4 и соответствующие им формулировки (3.1) и (3.2), можно сформулировать теорему 4(обобщённую теорему Пифагора).
|
Теорема 4 (обобщённая теорема Пифагора – формулировка на языке площадей подобных фигур) |
|
Сумма площадей подобных фигур, построенных на катетах прямоугольного треугольника, равна площади подобной им фигуре, построенной на гипотенузе. (4) |
Доказательство этой теоремы рассмотрено в задаче №2.
3. ОБОБЩЁННАЯ ТЕОРЕМА ПИФАГОРА
Задача № 2. Обобщённая теорема Пифагора
Постановка задачи
Доказать теорему 4, которая является обобщением теоремы Пифагора (3.1).
Комментарии к постановке задачи
Такими подобными фигурами могут быть не только квадраты, как в теореме Пифагора (3.1), но и любые другие правильные многоугольники: треугольники (см. рис. 6), пятиугольники, шестиугольники (см. рис. 8) и т. д. Такими фигурами могут быть и круги, полукруги (см. рис. 7) и любые подобные между собой фигуры (см. рис. 5).
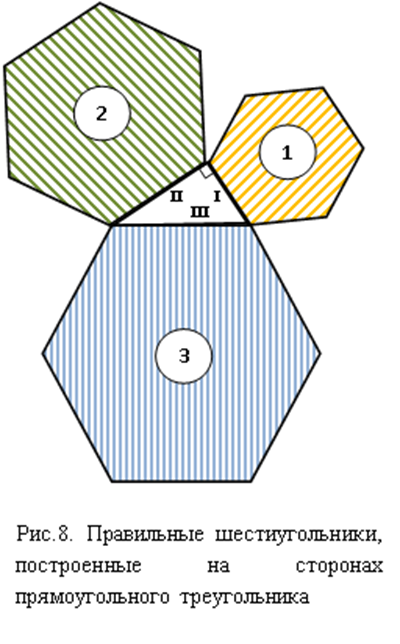
Здесь
I,
II,
III
– стороны прямоугольного треугольника. III
– гипотенуза;
![]() – площадиподобных
фигур, построенных на катетах прямоугольного треугольника;
– площадиподобных
фигур, построенных на катетах прямоугольного треугольника;
![]() – площадьфигуры,
подобной фигурам 1 и 2, построенной на гипотенузе прямоугольного
треугольника.
– площадьфигуры,
подобной фигурам 1 и 2, построенной на гипотенузе прямоугольного
треугольника.
Решение (доказательство)
Доказательство обобщённой теоремы Пифагора (4) с использованием анализа размерностей аналогично доказательству теоремы Пифагора (3).
На основании теоремы Пифагора имеем
На основании теоремы 1 о площадях подобных фигур имеем
Выразив из (5) квадраты сторон прямоугольного треугольника и подставив их в (4), получим
Умножив
обе части выражения (6) на число
![]() ,
получим
,
получим
|
. (ИФ7) |
Теорема доказана (задача решена).
Очевидно, что теорема 4 включает в себя теорему Пифагора (3.1), сформулированную на языке площадей квадратов, и имеет по сравнению с ней большую общность.
4. ТЕОРЕМА ГИППОКРАТА
Задача № 3. Теорема Гиппократа
На уроках геометрии (или физики) после доказательства обобщённой теоремы Пифагора можно предложить задачу, известную под названием «Теорема о лунках Гиппократа». При решении этой задачи обобщённая теорема Пифагора используется применительно к полукругам. Заметим, что все полукруги являются подобными фигурами.
Постановка задачи
Доказать теорему 5 (теорему Гиппократа).
|
Теорема 5 (теорема Гиппократа) |
|
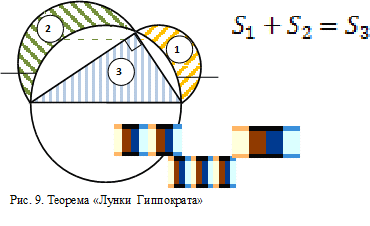
Сумма площадей фигур, образованных полуокружностями, построенными на сторонах прямоугольного треугольника, как на диаметрах, равна площади этого треугольника. (5) |
Лунками
Гиппократа называют серповидные фигуры, образованные пересечением
полуокружностей, построенных на сторонах
![]() как на диаметрах полуокружностей. Постановка задачи проиллюстрирована
рисунком 9.
как на диаметрах полуокружностей. Постановка задачи проиллюстрирована
рисунком 9.
Указания к доказательству
При доказательстве теоремы Гиппократа применение анализа размерностей сочетается с традиционными методами решения задач геометрии и логикой. Такое сочетание расширяет эффективность использования анализа размерностей. Доказательство этой теоремы здесь не приводится. Отметим лишь, что использование рисунков 7 и 9 здесь играет ключевую роль наряду с использованием обобщённой теоремы Пифагора (4).
С позиций геометрии эта задача характерна тем, что сумма площадей двух криволинейных фигур (лунок) равна площади фигуры с прямолинейными границами (прямоугольного треугольника).
Решение задач № 2 и 3 без использования анализа размерностей более сложное.
ЗАКЛЮЧЕНИЕ
Из этих примеров следует, что сочетание активной формы использования анализа размерностей с традиционными приёмами геометрии приводит к новым теоремам, к новым уровням обобщения наших знаний в геометрии. Такие обобщения способствуют более глубокому освоению учениками тем «геометрическое подобие» и «теорема Пифагора».
Предложенные задачи можно использовать как на уроках физики, так и на уроках геометрии. Они иллюстрируют возможности анализа размерностей и межпредметных связей.
Литература:
Аленицын А.Г., Бутиков Е.И., Кондратьев А.С. Краткий физико-математический справочник. – М.: Наука, 1990. – 368 с.
Иванов Б.Н. Законы физики. – М.: Высш. шк., 1986. – 335 с.
Баренблатт Г.И. Анализ размерностей: Уч. пос. – М.: МФТИ, 1987. – 168 с.
Неграш А.С., Мазейкина М.Ю. Сборник трудов докладов Всероссийского Съезда учителей физики. Москва, МГУ, 2011. – с.332-334
Похожие статьи
Теорема Стюарта и применение её для решения задач
Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
П. С. Моденов, Экзаменационные задачи по математике с анализом их решения, Москва «Книга по требованию».
Некоторые способы активизации мыслительной деятельности...
Теорема Стюарта и применение её для решения задач. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
Противоречивые задачи в школьном курсе математики
Рассмотрим следующую задачу: Сумма катетов прямоугольного треугольника равна 16 см, гипотенуза равна 10 см. Найти произведение синусов острых углов треугольника.
Доказательства теоремы Пифагора с точки зрения психологии
В современных учебниках геометрии теорема написана так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Доказательства теоремы Пифагора.
Интегрированный урок на тему «Треугольник и его виды»
Теорема Стюарта и применение её для решения задач. Дано: АВС-равнобедренный треугольник, АД-медиана к боковой стороне. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
Переопределенные задачи в школьном курсе математики
Теорема доказана (задача решена). 2.анализ решения задачи. Здесь I, II, III – стороны прямоугольного треугольника.
Рассмотрим следующую задачу: Сумма катетов прямоугольного треугольника равна 16 см, гипотенуза равна 10 см. Найти произведение...
Решение задач с применением метода геометрических...
Теорема Стюарта и применение её для решения задач. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
GeoGebra как средство решения стереометрических задач
Решение задачи, неважно какой сфере она принадлежит, начинается с её анализа: выделения условия (что дано) и вопроса (что найти/доказать).
Применяя теорему Пифагора, построим прямоугольный треугольник, катет которого будет иррациональным числом равным .
Решение задач строительной механики по определению...
соответствует правильному треугольнику, точка 1 — равнобедренному прямоугольному треугольнику; кривая 0–1
‒ подобрать функцию вида F = KQ(Kf)n, где Q обобщенная физико-геометрическая константа для конкретной рассматриваемой задач теории пластинок
Похожие статьи
Теорема Стюарта и применение её для решения задач
Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
П. С. Моденов, Экзаменационные задачи по математике с анализом их решения, Москва «Книга по требованию».
Некоторые способы активизации мыслительной деятельности...
Теорема Стюарта и применение её для решения задач. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
Противоречивые задачи в школьном курсе математики
Рассмотрим следующую задачу: Сумма катетов прямоугольного треугольника равна 16 см, гипотенуза равна 10 см. Найти произведение синусов острых углов треугольника.
Доказательства теоремы Пифагора с точки зрения психологии
В современных учебниках геометрии теорема написана так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Доказательства теоремы Пифагора.
Интегрированный урок на тему «Треугольник и его виды»
Теорема Стюарта и применение её для решения задач. Дано: АВС-равнобедренный треугольник, АД-медиана к боковой стороне. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
Переопределенные задачи в школьном курсе математики
Теорема доказана (задача решена). 2.анализ решения задачи. Здесь I, II, III – стороны прямоугольного треугольника.
Рассмотрим следующую задачу: Сумма катетов прямоугольного треугольника равна 16 см, гипотенуза равна 10 см. Найти произведение...
Решение задач с применением метода геометрических...
Теорема Стюарта и применение её для решения задач. Найти: стороны треугольника АВС. Решение: Так как АВС — прямоугольный треугольник, то гипотенуза АВ=2R, значит АВ=30см.
GeoGebra как средство решения стереометрических задач
Решение задачи, неважно какой сфере она принадлежит, начинается с её анализа: выделения условия (что дано) и вопроса (что найти/доказать).
Применяя теорему Пифагора, построим прямоугольный треугольник, катет которого будет иррациональным числом равным .
Решение задач строительной механики по определению...
соответствует правильному треугольнику, точка 1 — равнобедренному прямоугольному треугольнику; кривая 0–1
‒ подобрать функцию вида F = KQ(Kf)n, где Q обобщенная физико-геометрическая константа для конкретной рассматриваемой задач теории пластинок