Технология развивающего обучения в вузах

В статье рассмотрена технология развивающего обучения в вузах на примере теоретической механики, которая в технических высших учебных заведениях преподается на первых — вторых курсах.

Ключевые слова: технология, развивающее обучение, технические вузы

 

Keywords: technology, developing training, technical colleges

 

Под развивающим обучением автор понимает создание условий для активно-деятельностной работы студентов над изучаемыми научными дисциплинами, в частности над теоретической механикой, с целью совершенствования их инженерной, профессионально-практической, творческой и мировоззренческой подготовки.

Составные части технологии указаны в названиях разделов статьи.

1.      Усиление теоретической подготовки студентов.

Автор сделал краткий экскурс в историю развития механики, чтобы показать, что явления механики изучали и открывали ведущие ученые мира, которые публиковали свои открытия и обучали на них своих учеников. Например, древнейший ученый Архимед (III в. до н. э.) изложил свои изыскания по механике в сочинении «О рычагах». Французский механик Л. Пуансо разработал новые элементы статики и изложил их в трактате “Элементы статики”, который вышел в 1804 г. Итальянский ученый Галилей изложил свои изыскания по механике в труде «Механика» (1593). Английский ученый И. Ньютон сформулировал основные законы динамики и изложил их в своем трактате «Математические начала натуральной философии», вышедшем в 1687 г. Ньютон подытожил достижения своих предшественников и указал пути дальнейшего развития механики. Ученый Л. Эйлер издал свой труд «Механика» (1736). Лагранж, который в двухтомном сочинении «Аналитическая механика» (1788) рассмотрел аналитическую динамику несвободной системы. Такой же подход к механике наблюдается и у русских ученых. Софья Ковалевская — «Задача о движении твердого тела вокруг неподвижной точки» (1888). В сочинении Н. Е. Жуковского «О прочности движения» (1882 г.). Совместно с Н. Е. Жуковским работал С. А. Чаплыгин, который также внес большой вклад в развитие авиации. Он защитил докторскую диссертацию на тему «О газовых струях». Рассмотрение важнейших задач теории устойчивости движения принадлежат А. М. Ляпунову, которые изложены им в фундаментальном труде «Общая задача об устойчивости движения» (1892).

Ученик Н. Е. Жуковского и С. А. Чаплыгина И. М. Воронков, ставший профессором в 1930 году, написал учебник «Курс теоретической механики» [1], претерпевший большое количество изданий, и используемый как в нашей стране, так и за рубежом.

В 1958 г. появился учебник для высших технических учебных заведений С. М. Тарга [2] «Краткий курс теоретической механики». Учебник С. М. Тарга стал одним из основных учебников по теоретической механике. Он выдержал уже 15 изданий в нашей стране и переведен на 14 языков мира.

В 1962 появился учебник «Курс теоретической механики» А. А. Яблонского [3], который претерпел также большое количество изданий, и используется как в нашей стране, так и за ее пределами. Широко используется и пособие для курсовых работ, разработанное под руководством и непосредственном участии профессора А. А. Яблонского [4].

Существует еще большое количество учебников и учебных пособий в нашей стране, написанных замечательными учеными и методистами. Автор преследовал единственную цель в этом кратком обзоре — показать, что с развитием общества, и по мере развития механики, учебники по этой науке составлялись ведущими учеными мира. Они имеют весьма высокий уровень изложения теоретических вопросов по всем разделам механики. Такая традиция сохранилась до настоящего времени. Студенты имеют прекрасную возможность овладевать законами классической механики и быть грамотными специалистами.

Занимаясь теоретической механикой со студентами, автор, однако, заметил один существенный недостаток существующих учебников и учебных пособий, они все рассматривают неизменяемые схемы механизмов, устройств, конструкций, не позволяющих проводить студентам научные исследования. Научные же исследования усиливают значение теории по теоретической механике особенно для студентов первых курсов, поэтому автор решил устранить этот недостаток включением в пособие [5] заданий исследовательского характера.

Гносеологические аспекты опытов весьма объективно выражены профессором А. А. Космодемьянским: «История науки показывает, что внутренние количественные закономерности новых реальных явлений природы и техники, подвергающиеся систематическому изучению, не всегда могут быть адекватно переданы закономерностями уже известных математических алгоритмов и операций, рожденных, быть может, другими реальными связями и отношениями. Поэтому изучение явлений путем постановки опытов является в теоретической механике началом многих наиболее прогрессивных теорий».

По ходу изложения материала по теме сходящихся сил доказывается теорема о трех силах. Для проверки полученных результатов разработана экспериментальная установка [6], схема которой представлена на рис. 1.

Установка содержит станину, состоящую из цилиндрической направляющей 1, закрепленной в стойках 2. На цилиндрической направляющей расположены клеммы 3, 4 и 5. С клеммой 3 шарнирно соединен стержень 6, на который наклеен тензодатчик 7. Другой конец стержня 6 шарнирно связан с пластинами 8 и подвесом 9 с грузом 10 (см. также разрез «А-А»). Шарнирное соединение стержня 6, пластин 8 и подвеса 9 осуществляет палец 11, который удерживается от осевого перемещения шайбами 12 и шплинтами 13. В пазах пластин 8 расположен палец 14 с лысками под ключ (см. разрез «Б-Б»), который одновременно находится в отверстиях клеммы 4. Пластины 8 жестко закреплены к пальцу 14 посредством резьбовых крепежных элементов 15 и 16. На пластины 8 наклеены тензодатчики 17.

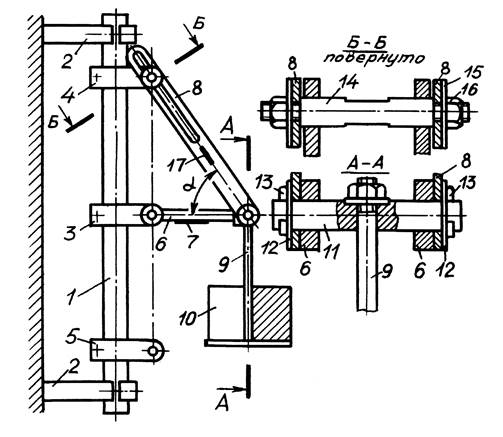
Рис. 1. Схема экспериментальной установки

 

Перемещением клемм, например, 3 и 4 вдоль направляющей станины 1 и закреплением их в нужном положении, а также перемещением пластин 8 относительно пальца 14 и закреплением их резьбовыми крепежными элементами 15 и 16 в нужном положении получают одну из систем стержней, изображенных на рис. 1.1 и 1.2, а, б. Поместив груз 10 на подвес 9, с помощью тензодатчиков 7 и 17, а также тензометрической аппаратуры, которая на схеме не показана, измеряют усилие в стержне 6 и 8.

Чтобы получить системы стержней, изображенные на рис. 2, в-д, достаточно пластины 8 перекинуть с клеммы 4 на клемму 5 (рис. 1).

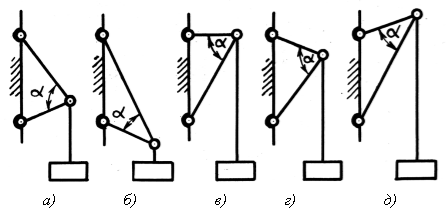
Рис. 2. Схемы стержневых систем

 

Кроме исследования различных видов стержневых систем, изменением углов a можно исследовать экспериментально зависимость возникающих сил в стержнях от углов их наклона.

На рис. 3 представлены результаты теоретического и экспериментального исследований сил в стержнях системы, представленной на рис. 2, в, при изменении угла a наклона стержня ВС. После построения силового треугольника силы, возникающие в стержнях, определены по формулам

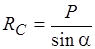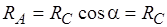; ∙ ctga.                                                         (1)

Экспериментальные данные получены с помощью установки, представленной на рис.1.

Автор включает в пособие такие задания исследовательского характера, которые имели хотя бы одно готовое исследование, а остальные возможные случаи исследований студенты осуществляли бы самостоятельно.

Убедившись в эффективности подобных заданий для развития студентов, автор разработал устройства с изменяемыми линейными параметрами почти по всем темам теоретической механики.

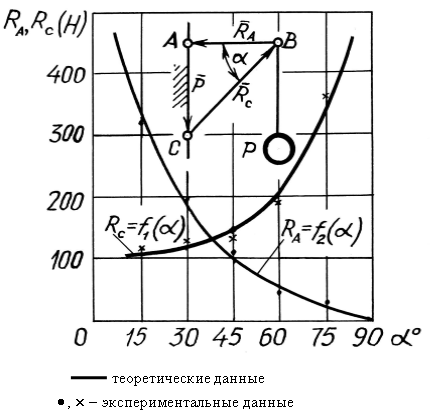
Рис. 3. Графическая зависимость усилий в стержнях от угла a наклона стержня ВС

 

2.      Индивидуализация аудиторных и домашних заданий студентам.

Она заключается в том [7], что студенты получают индивидуальные задания: аудиторные (на практических занятиях, на занятиях по самоподготовке) или домашние (для изучения и решения задач в домашних условиях). Этот прием был реализован первоначально в пособии [8, 18], в котором материал раздела «Статика» разделен на 13 тем, материал раздела «Кинематика» - на 14 тем, а раздел «Динамика» - на 18 тем (всего 45 тем). Для каждой темы сформулированы вопросы для изучения, представлена литература, по которой студенты должны изучать требуемый материал и решать на эту тему задачи. Для каждой темы составлены контрольные карты с вопросами и задачами (по 30 карт к каждой теме). Ниже представлены примеры тем статики.

Занятие № 1

Раздел: статика твердого тела.

Тема: история развития и основные понятия и определения механики.

Вопросы:

1.      Механика — наука о механическом движении и взаимодействии материальных тел.

2.      История развития механики.

3.      Основные понятия и определения механики и статики.

4.      Понятие силы и классификация сил.

5.      Аксиомы статики.

Рекомендуемая литература

1.      Маркин Ю. С., Петрушенко Ю. Я. Теоретическая механика, часть I, Статика твердого тела: Учеб. пособие. — 2-е изд., перераб. и доп. — Казань: КГЭУ, 2006. § 1.1, 1.2.

2.      Тарг С. М. Краткий курс теоретической механики. — М.: Наука, 1972. § 18,19; § 42, 45.

3.      Яблонский А. А. и Никифорова В. М. Курс теоретической механики. — М.: Издательство «Лань», 2002. § 19, 14–16.

Составить краткий конспект теоретических вопросов и решить задачи, приведенные в рекомендуемой литературе.

К каждой теме составлены контрольные карты, на вопросы которых должны отвечать студенты.

Примеры контрольных карт к занятию № 1

Занятие № 1

Статика Контрольная карта № 1

1.      Дайте определение силы.

2.      Сформулируйте первую аксиому статики.

3.      Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.

4.      Кто является основоположником статики?

Занятие № 1

Статика Контрольная карта № 2

1.      Дайте определение системе сил.

2.      Сформулируйте вторую аксиому статики.

3.      Дайте определение абсолютно твердому телу.

4.      Кто является основоположником теории механизмов и машин?

Пример контрольной карты по теме «Связи и реакции связей.

Занятие № 2

Статика Контрольная карта № 1

1.      Дайте определение несвободного твердому телу.

2.      Нанесите реакции связей (рис. 4).

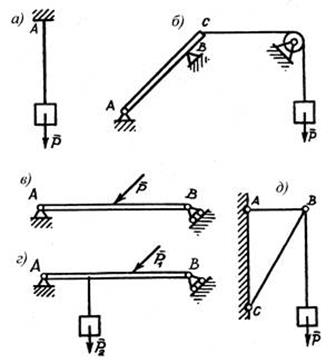
Рис. 4. Схемы вариантов заданий

 

Примеры контрольных карт к теме «Сложение сходящихся сил»

Сходящиеся силы можно складывать геометрически с помощью аксиомы о параллелограмме сил и построением силового многоугольника, а также аналитически. Это и предусмотрено в каждом индивидуальном задании.

Занятие № 3

Статика Контрольная карта № 1

1.      Дайте определение системе сходящихся сил.

2.      Сложите силы с помощью аксиомы о параллелограмме сил, векторным многоугольником и аналитически (рис. 5).

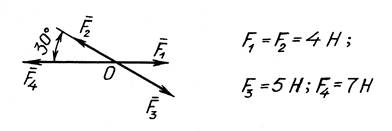
Рис. 5. Схема сходящейся системы сил

 

Занятие № 3

Статика Контрольная карта № 2

1.      Как геометрически складываются две силы, приложенные к телу в одной точке под углом α?

2.      Сложите силы с помощью аксиомы о параллелограмме сил, векторным многоугольником и аналитически (рис. 6).

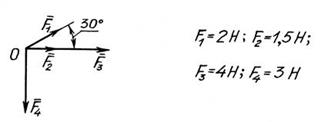
Рис. 6. Схема сходящейся системы сил

 

И так в каждом из 13 занятий. Аналогичные пособия составлены по кинематике [9, 8] (14 занятий) и по динамике [10, 5] (18 занятий).

Первоначально проверка студенческих ответов на вопросы контрольных карт производилась непосредственно преподавателем. Учитывая, что это очень трудоемкая работа, автор составил тесты по каждому разделу теоретической механики, например, [11, 4]. Со временем автор убедился в целесообразности преобразования тестов в форму вопросов и ответов и составил три новых пособия [12, 5; 13, 6; 14, 7].

Индивидуализация аудиторных и домашних заданий способствует обязательному их выполнению каждым студентом и отвечает условиям развивающего обучения.

3.      Исследовательская работа студентов.

Задания к расчетно-графическим работам автор выдавал по профессионально составленному и широко известному пособию [4, 7]. В этом пособии все задания (конструкции, устройства и механизмы) выполнены застывшими, т. е. с неизменяемыми линейными и другими параметрами, не позволяющими организовывать исследовательскую работу студентов. И только летом 2011 года автору пришла идея преобразовать представленные в пособии [4, 23] задания. Первым заданием, подвергшимся преобразованию, явилось «Задание С.3. Определение реакций опор составной конструкции». Все 30 схем превратились в конструкции с изменяемыми линейными параметрами, чтобы снабжать студентов заданиями исследовательского характера. На новые конструкции были оформлены заявки на полезные модели в Федеральный институт промышленной собственности (ФИПС) и получены соответствующие патенты, по которым позднее составлено пособие [15, 5]. В 2012 году такие задания были предложены одной из студенческих групп, с которыми автор занимался теоретической механикой. Перед студентами была поставлена задача — исследовать влияние размеров участков составных конструкций на величины реакций связей. Первые исследования студенты осуществляли вручную, например, [16, 135]. Исследования, выполняемые вручную, являются самыми полезными для студентов, поскольку все действия студентам приходится выполнять своими «пальчиками»: от изображения схем, нанесения реакций связей, составления уравнений равновесия и их решений, составления программы исследований, проведение исследований, заполнение соответствующих таблиц, построение графиков и до формулирования выводов о характере изменения реакций связей.

Несмотря на некоторое увеличение времени выполнения исследовательских заданий, к автору обратились студенты других групп как этого потока, так и групп лекционных потоков других институтов и факультетов. Автор в то время читал лекции на трех потоках, принадлежащих соответственно институту теплоэнергетики, институту электроэнергетики и электроники и факультету энергомашиностроения. Автор удовлетворил всех желающих. Ему было интересно знать, как будут выполнять исследования студенты разных институтов и факультетов. У него были некоторые сомнения об интеллектуальных возможностях студентов этих институтов и факультетов. В 2015 году он предложил задания исследовательского характера даже студентам заочного факультета, которые тоже все справились с индивидуальными задачами из книги [17, 23].

Учитывая важность начатой работы, автор настойчиво претворял ее в жизнь. Он руководствовался следующими соображениями:

-        развивать мышление и индивидуальные способности студентов;

-        научить студентов первых курсов владеть методикой научных исследований;

-        научить студентов планированию и проведению самостоятельных научных исследований;

-        улучшить инженерную подготовку студентов;

-        расширить научную эрудицию студентов и уверенно применять ее в своей профессионально-практической деятельности;

-        формировать диалектическое мышление студентов.

Ниже представлено исследование величин реакций связей от размеров участков твердого тела (ломаного стержня, рис. 4), выполненное студентом-заочником.

Дано: l₁ = 3 м, P₁ = 6 kH, P₂ = 10 kH, M = 12 kHм.

Решение: поскольку левая часть стержня жестко заделана в неподвижное твердое тело (станину), реакцию связи в точке А студент разложил на составляющие 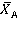 и 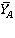. Кроме того, в жесткой заделке (в точке А) возникает момент жесткой заделки 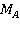. Получилось, что к конструкции приложена плоская произвольная система сил.

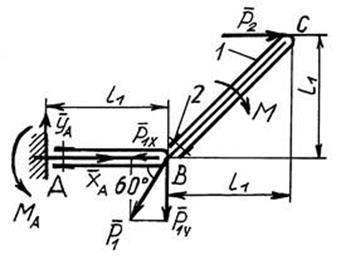
Рис. 7. Схема твердого тела с приложенными к нему силами и моментами

 

Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций действующих сил на каждую из координатных осей (х и у) равнялись нулю и алгебраическая сумма моментов сил относительно любого центра, лежащего в той же плоскости, тоже равнялась бы нулю.

Студент составил уравнения равновесия, решил их, осуществил соответствующие вычисления, заполнил таблицу.

По табличным данным он построил графики исследуемых величин (рис.8). Из построенного графика видно, что реакции связи Х_А и Y_A с увеличением участка АВ остаются постоянными, а момент M_A, возникающий в жесткой заделке, увеличивается.

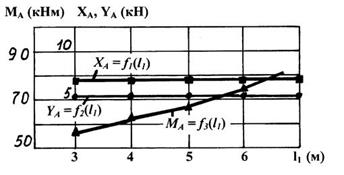
Рис. 8. Графики изменения реакций связей твердого тела

 

Автор постоянно совершенствует исследовательскую методику обучения студентов. Так, в 2013–2014 учебном году он работал со студентами Института экономики и информационных технологий по кафедре инженерной кибернетики. Студенты этого института (семь человек) составили 30 программ для исследования составных конструкций, описанных в пособии [15, 22]. Студенты, обучающиеся по прикладной математике, решали задачи по теоретической механике: вычерчивали схемы составных конструкций, наносили на них реакции связей, составляли уравнения равновесия, которые решали, а затем составляли соответствующие программы для исследования реакций связей этих конструкций. Все составленные программы зарегистрированы в ФИПСе. Таким образом, автор проверил возможность заниматься исследовательской работой студентов всех институтов и факультетов Казанского государственного энергетического университета.

Ниже (рис. 9) представлен пример выполнения исследований составной конструкции студентом Саяповым Артуром (группа ЭЭ-2–13) на компьютере с помощью составленной программы.

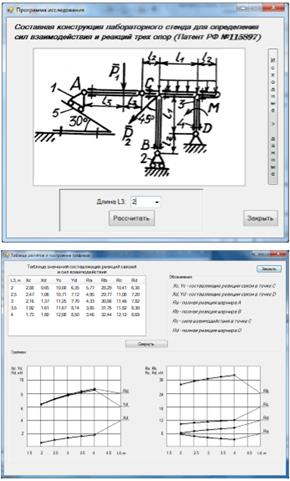
Рис. 9. Результаты исследования составной конструкции с помощью компьютера

 

В результате проделанной работы автор убедился в необходимости привлечения студентов к исследовательской работе, которая также является элементом развивающего обучения студентов первых курсов. Для этой цели автор подготовил несколько книг с заданиями исследовательского характера [17–21].

4.      Привлечение студентов к творческой работе в коллективе.

Руководя исследовательской работой студентов, автор заметил, что они хорошо владеют компьютерной графикой, и решил привлечь их к творческой работе. Они исследовали в это время составные конструкции, поэтому изучили их свойства, методы исследования, устройство и другие характеристики. В пособии [4, 28] представлены более сложные составные конструкции. Вот эти конструкции автор и решил предложить студентам совершенствовать: сначала задание С.4, названное как система трех тел, а затем задание С.9. Составные конструкции с внутренними односторонними связями. Студенты охотно согласились. Для этой работы был создан кружок студенческого научного общества (СНО) при кафедре «Механика», а затем при кафедре «Динамика и прочность машин». Каждую схему автор выдавал группе студентов. Каждый студент группы предлагал свою новую схему. Мы собирались во вне учебное время, обсуждали и выбирали наиболее совершенный вариант схемы. Иногда вносили коррективы. После этого составляли заявку на полезную модель и отсылали в ФИПС. При изучении кинематики студенты участвовали в совершенствовании шарнирно-рычажных механизмов (Задание К.4) [4, 80]. В 2012 году было подготовлено 100 заявок и получено столько же патентов Российской Федерации на полезные модели. Благодаря такой работе Казанский государственный энергетический университет среди вузов Республики Татарстан занял первое место. В течение 2013 и 2014 годов кружок СНО выдавал ежегодно также по 100 патентов, а автор разработал новую методику преподавания теоретической механики: «От научных исследований — к разработке учебного оборудования».

В связи с положительными результатами обучения студентов, автор продолжает разрабатывать задания исследовательского характера. За последнее время им разработаны схемы твердых тел [17, 35] и механизмы с изменяемыми линейными параметрами [21, 23], а также задания по следующим темам:

1.      Детали и устройства с изменяемой геометрией.

2.      Шарнирно-рычажные механизмы.

3.      Стенды для исследования сложного движения точки.

4.      Устройства для исследования относительного движения точки.

5.      Устройства для исследования их принципом Даламбера.

6.      Устройства для исследования их принципом возможных перемещений.

Поскольку заданий исследовательского характера скопилось уже много, автор приступил к разработке справочника по таким механизмам.

5.      Профессиональная ориентация решаемых задач.

Проводя практические занятия по теоретической механике, автор заметил, что если задачи носят общий характер, то студенты несколько инертно относятся к их решению, но стоит представить им задачу, перекликающуюся по содержанию с их будущей профессиональной деятельностью, это их оживляет, они начинают проявлять интерес к задаче и решение задач проходит более интенсивно. Студенты задают вопросы, предлагают какие-то новые условия задачи, пытаются получить другие решения и т. д. Автор подготовил такой сборник задач, работая еще в сельскохозяйственных вузах, а опубликовать его [22, 10] удалось недавно. Интересуясь такой проблемой, автор обнаружил, что она волнует не только его, а многих преподавателей теоретической механики. Так, в Нижегородском государственном университете им. Н. И. Лобачевского провели специальное исследование [23, 3], в котором отметили, что при решении задач «включаются все мыслительные процессы: внимание, восприятие, память, воображение, мышление. В этом реализуется развивающая функция упражнений в решении задач».

6.      Включение в учебный процесс элементов проблемного обучения.

Элементы проблемного обучения автором использованы при составлении лабораторных практикумов [24, 3; 25,3; 26,3].

В работах использованы установки с легко изменяемыми параметрами, что позволяет организовать проведение студентами учебных исследований. Каждая работа предполагает, кроме того, самостоятельную настройку студентами лабораторной установки. Такой подход к выполнению лабораторных работ развивает у студентов навыки самостоятельной практической работы сначала с лабораторным, а затем и промышленным оборудованием.

Методические указания к работам представлены в проблемной постановке, например, «Влияние углов наклона стержней на величины возникающих в них усилий под действием внешней нагрузки». Решение главной проблемы, кроме того, сопровождается дополнительными проблемными ситуациями, помогающими студентам осуществлять промежуточный самоконтроль и самостоятельно выходить из возможных затруднений, например, путем сравнения результатов теоретического и экспериментального исследований, путем измерения некоторых параметров несколькими методами и т. д.

Проблемность постановки лабораторных работ заключается и в том, что студенты по представленным кинематическим схемам должны изучить устройство установок и применить их для экспериментального исследования соответствующих явлений. В каждой работе предусмотрено использование вычислительной техники (микрокалькуляторов или ПЭВМ). Такой подход к выполнению работ, по нашему мнению, дает возможность организовать сравнение результатов теоретических исследований с результатами экспериментальных исследований.

Важной особенностью описанных лабораторных работ является и то, что они направленно формируют диалектическое мышление студентов, их личностные и деловые качества, развивают практические навыки и самостоятельность.

Возможность проведения учебных исследований, приобретение практических навыков работы с оборудованием, проблемная постановка лабораторных работ, использование вычислительной техники, активное формирование диалектического мышления студентов и другое делают лабораторный практикум направленным на интенсификацию учебного процесса и повышение качества подготовки специалистов для народного хозяйства страны. Этим лабораторные работы составляют компонент развивающего обучения.

«Хотя преподавателю с самого начала известен кратчайший путь к решению проблемы [27], его задача — ориентировать сам процесс поиска, шаг за шагом приводя студентов к решению проблемы и получению новых знаний. Некоторые авторы определяют проблемное обучение как ряд проблемных задач, последовательное решение которых ведет к достижению поставленной дидактической цели.

Проблемные задачи выполняют тройную функцию:

-        они являются начальным звеном процесса усвоения новых знаний;

-        обеспечивают успешные условия усвоения;

-        представляет собой основное средство контроля для выявления уровня результатов обучения».

Ниже представлен пример лабораторной работы из лабораторного практикума по теоретической механике [24, 3], который составлен по поручению семинара-совещания заведующих кафедрами, состоявшегося в Киевском политехническом институте в 1988 году.

Работа № 14

Динамическая балансировка вращающихся тел

Работа посвящена динамическому уравновешиванию вращающихся масс.

Целью работы является экспериментальное уравновешивание роторов и выявление зависимости амплитуды колебания маятниковой рамы балансировочного станка от дисбаланса ротора.

При выполнении этой работы студенты приобретают навыки работы с балансировочной техникой.

Работа необходима для организации уравновешивания роторов различных машин при их ремонте.

Описание установки

Балансировочный станок (рис.10) состоит из маятниковой рамы 1, опирающейся на пружину 2 и закрепленной шарнирно к станине в точке 0. Балансируемый ротор 3 устанавливается в подшипники 4, жестко связанные с маятниковой рамой. Станок снабжен регистрирующим устройством 5 и приводом, который состоит из клинового ремня, надетого на шкив электрического двигателя, и ролик, укрепленный на подвижном рычаге (привод на схеме не показан).

Маятниковая рама состоит из труб, жестко связанных между собой клеммами. Со станиной рама соединена двумя шарнирами, каждый из которых состоит из двух взаимно перпендикулярных пластин, исключающих ее колебание в горизонтальном направлении.

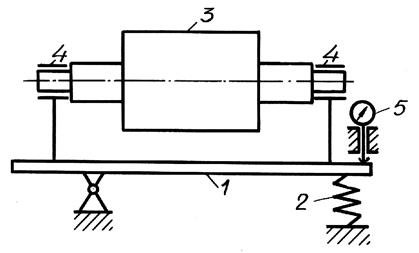
Рис. 10. Схема балансировочного станка

 

Если маятниковую раму при неподвижном роторе вывести из состояния покоя, она будет совершать свободные колебания. С течением времени амплитуда таких колебаний затухает, а период остается постоянным.

При вращающемся неуравновешенном роторе маятниковая рама совершает вынужденные колебания. Период таких колебаний равен времени одного оборота ротора, а амплитуда зависит от динамических давлений, от сопротивлений движению и от отношения периода Т изменения динамических давлений (возмущающих сил) к периоду Т_о свободных колебаний, т. е. Т/T_о. Если Т/Т_о = 1, то возникает резонанс, а амплитуда колебаний значительно возрастает и оказывается наибольшей. При этом даже небольшое по величине динамическое давление вызывает колебание рамы с увеличенной амплитудой. На явлении резонанса и основана работа описываемого балансировочного станка, т. е., если при выбеге ротора, у которого Т < Т_о, резонанс появляется, это говорит о том, что ротор неуравновешен; если резонанс не возникает — ротор уравновешен.

Теория вопроса

Тело массы М (рис. 11) вращается вокруг неподвижной оси z₁ под действием приложенных к нему сил 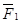, ,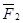.... 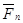с угловой скоростью w и угловым ускорением e. Необходимо найти реакции подшипников в точках А и В.

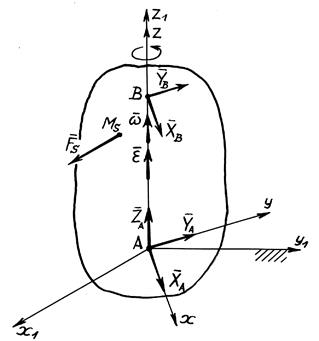
Рис. 11. Схема вращающегося тела

 

Свяжем неподвижно с телом координатные оси xyz и на них разложим реакции R_A и R_B.

Применив теорему о количестве движения:

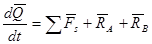                                                                                                  (2)

и теорему моментов:

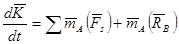,                                                                                         (3)

а также используя для каждого случая теорему Бура, получают шесть уравнений, по которым определяют требуемые реакции.

Эти уравнения имеют вид:

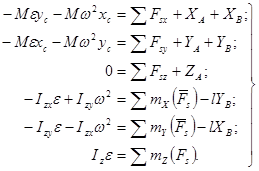                                                                      (4)

Члены, выделенные штриховыми линиями в уравнениях (4), определяют дополнительные динамические реакции подшипников на тело (ротор).

Если эти члены будут равны нулю, то тело будет уравновешенным, т. е.,

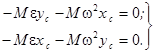 (5)

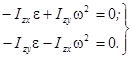 (6)

Решив определители, составленные из уравнений (5) и (6), получают, соответственно, два условия:

x_C = y_C = 0                                                                                                                     (7)

и

J_ZX = J_ZY = 0,                                                                                                                  (8)

определяющие уравновешенность тела.

Эти условия показывают, что для динамической уравновешенности тела необходимо и достаточно, чтобы ось вращения тела являлась главной центральной осью инерции.

Для практических целей важен и другой вывод: любую ось, проведенную в теле, можно сделать главной центральной осью инерции прибавлением к телу двух точечных масс.

Установка ротора и определение уравновешивающих грузов

Ротор для уравновешивания устанавливается на станке первоначально так (рис. 12), чтобы одна из плоскостей уравновешивающих грузов, например, плоскость е« проходила через ось, относительно которой колеблется маятниковая рама. В этом случае момент от динамических давлений Q_д¢¢, возникающих в этой плоскости, относительно оси качания равен нулю. Маятниковая рама совершает вынужденное колебательное движение только под действием момента от динамических давлений Q_д¢, возникающих в плоскости уравновешивающих грузов е'. Однако, если в плоскости е' прикрепить уравновешивающий груз, то колебания исчезнут.

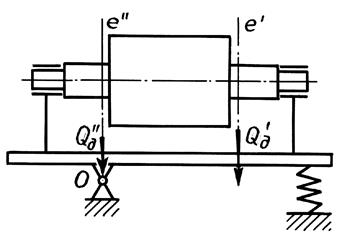
Рис. 12. Схема установки ротора на маятниковую раму первоначально

 

Определение уравновешивающих грузов можно разделить на два этапа: 1) определение места расположения груза и 2) определение веса груза.

Для определения места расположения груза на роторе делают разметку, как показано на рис. 10.4, и намечают четыре точки: А, В, С и D. Затем берут кусок пластилина произвольного веса, но прямоугольной формы, и поочередно прикрепляют его в намеченных точках, измеряют амплитуды колебания и записывают их на роторе около соответствующих точек. Например, в результате измерений в точках А, В, С и D амплитуды колебаний оказались, соответственно, равны 5, 7, 15 и 12 делениям шкалы индикатора. Сравнивая полученные данные, приходим к выводу, что груз надо располагать между точками А и В, но ближе к А. В этой зоне надо наметить еще несколько точек и, производя измерения, надо найти такое положение груза, в котором амплитуда колебаний будет минимальной.

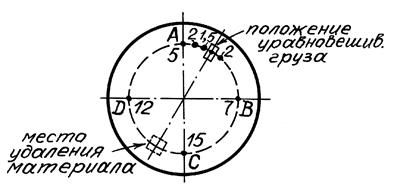
Рис. 13. Схема разметки ротора

 

Изменением веса пластилина (срезанием или добавлением) добиваются такой амплитуды, которая не будет превышать допустимой.

Затем пластилин заменяют металлическим грузом. Часто прикрепление уравновешивающего груза заменяют удалением соответствующего количества материала с противоположной стороны. Однако это возможно только тогда, когда плоскость е' пересекает тело ротора.

После этого ротор уравновешивают описанным образом в плоскости е¢¢ (рис. 14). При этом положение плоскости e' нe имеет никакого значения, т. к. динамические давления ротора на маятниковую раму в этой плоскости после уравновешивания равны нулю.

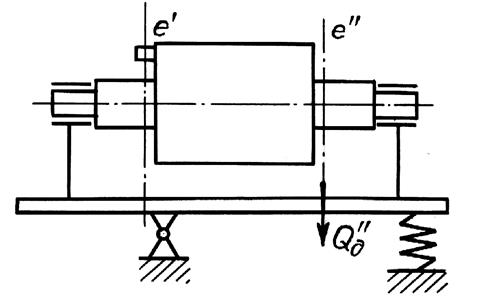
Рис. 14. Схема установки ротора для уравновешивания в плоскости е^’’

 

Произведение веса G уравновешивающего или какого-либо другого груза на расстояние r от его «центра массы» до оси вращения называют дисбалансом:

D= GrГсм.                                                                                                                 (9)

Чтобы получить зависимость между дисбалансом ротора и амплитудой колебания маятниковой рамы, необходимо к уравновешенному ротору прикреплять различные грузы на одинаковом расстоянии от оси вращения или один и тот же груз на различных расстояниях.

Практическая часть

1.      Составить программу опытов.

В программе предусмотреть уравновешивание ротора и отыскание экспериментальным путем зависимости амплитуды колебания маятниковой рамы от дисбаланса ротора.

2.      Изучить устройство станка для динамической балансировки и принцип его работы.

3.      Установить ротор.

4.      Осуществить пробный пуск.

5.      Найти местоположение и величину уравновешивающего груза в одной из плоскостей ротора.

6.      Провести намеченное исследование.

7.      Сделать выводы.

Список рекомендуемой литературы

1.       Шитиков Б. В. Основы теории механизмов./ Учебное пособие — Казань: Казанский химико-технол. ин-т, 1970, вып. III, с. 23–33.

2.       Патент РФ № 32003. Станок для динамической балансировки / Маркин Ю. С., Наумов Л. Г., Маркин О. Ю. и др. МКИ В 04 В 9/14. Опубл. 10.09. 2003. Бюл. № 25.

Вопросы для самоконтроля

1.      Что такое статические и динамические давления подшипников на ротор, и от каких факторов они зависят?

2.      Какой ротор является уравновешенным?

3.      Как устроен станок для динамического уравновешивания роторов?

4.      На каком принципе основана работа этого станка?

5.      Как установить ротор на станке для его уравновешивания?

6.      Как найти уравновешивающие грузы?

7.      Что такое дисбаланс?

8.      Как отыскать зависимость амплитуды колебания маятниковой рамы от дисбаланса ротора?

9.      Как перейти от уравновешивания пластилином к уравновешиванию роторов металлическими грузами?

10.  В чем ошибочность механистических и метафизических представлений о строении материи?

11.  В чем заключается принцип относительности Галилея?

12.  Какие законы диалектики действуют в этой лабораторной работе?

8.      Формирование диалектического мышления студентов.

Автор давно и серьезно уделяет этому вопросу большое внимание. В творческом взаимодействии с коллегами кафедры философии им подготовлена и издана работа [33], в которой явления механики рассмотрены с диалектической точки зрения, т. е. с точки зрения законов и категорий диалектики.

Рассмотрев порядок изложения основных законов диалектики в философских работах Ф. Энгельса и В. И. Ленина, Б. М. Кедров пришел к выводу, что последовательность их изложения существенной роли не играет и что взаимосвязь между ними надо искать на другом направлении. Одновременно он предложил рассмотреть сущность процесса развития, т. е. ответить на три вопроса: 1) почему происходит развитие? 2) как оно осуществляется? 3) что получается в результате развития? В ответах на эти вопросы и кроется взаимосвязь между основными законами диалектики. Если в первом случае речь идет об установлении источника развития, то во втором — о раскрытии его внутренней детальной картины, а в третьем — о его форме. Иными словами, отвечая на вопрос «почему», мы должны показать «движущую пружину» процесса развития, отвечая на вопрос «как» — его механизм, а на вопрос «что получено» — «траекторию», пройденную в ходе развития. Однако следует отметить, что вскрыть процесс диалектического развития, показать, как он совершается и что образует при своем относительном завершении — это значит показать одну из сторон взаимосвязи основных законов диалектики.

Другой стороной взаимосвязи является тот диапазон, в пределах которого действует и проявляет себя в полной мере тот или иной закон. Анализ показывает, что закон единства и борьбы противоположностей (противоречие) действует и проявляет себя в любом месте (в любой точке) процесса развития, причем непрерывно. В противном случае развитие было бы прервано, остановлено и весь процесс прекратился бы. Следовательно, этот закон можно назвать дифференциальным. Другой закон перехода количественных изменений в качественные отличается от предыдущего тем, что проявляет свое действие не везде, а только в пределах отдельных его отрезков, участков, промежутков времени.

Пока идет процесс количественных изменений, действие этого закона не обнаруживается. Этот закон обнаруживает себя только тогда, когда быстро и резко наступает превращение количественных изменений в качественные (фаза скачка). Этот закон называют дифференциально-интегральным.

И, наконец, третий закон — закон отрицания отрицания. Этот закон, как и два предыдущих, действует в ходе всего процесса развития, а обнаруживает свое действие лишь после повторного отрицания, т. е. в самом конце рассматриваемого процесса, когда достигнет своего относительного завершения. Это происходит в тот момент, когда заканчивается очередной виток спирали и развитие достигает своего исходного пункта на новой основе. Поскольку этот закон охватывает весь путь, пройденный процессом развития, и суммирует все результаты развития, его называют интегральным.

Методологическое значение законов диалектики для студентов заключается в том, что они дают ключ к пониманию процесса развития не только всего материального мира, но в первую очередь собственного развития в процессе обучения.

В процессе обучения возникает много противоречий. Возникает и такое противоречие, как противоречие между массовостью системы высшего образования в стране и необходимостью качественной индивидуальной подготовки специалистов для народного хозяйства. Или: 1) противоречие между большими психическими и физическими возможностями и небольшим жизненным опытом большинства студентов; 2) противоречие между обилием и широтой получаемой информации и глубиной ее переработки; 3) противоречие между относительной свободой в организации самостоятельной умственной деятельности и необходимостью иметь жесткий и четкий распорядок своей учебной и вне учебной деятельности и т. д.

В решении этих и других противоречий, а также в их взаимном переходе и заключается процесс движения, развития и обучения студентов. И если каждый студент поймет, что интенсивность и качество его развития зависит от самодвижения, саморазвития, то эффект обучения будет обеспечен, а цель — достигнута.

Для успешного обучения студентам важно понять и пользоваться другим законом диалектики: перехода количественных изменений в качественные. Они должны понять, что без количественного накопления знаний не обойтись, что накопленное количество знаний дает на определенных этапах развития качественные скачки, т. е. студенты приобретают по определенным предметам соответствующие знания, умения, навыки и привычки (внешне это проявляется в сдаче заданий, зачетов и экзаменов). Наиболее сильный и резкий скачок происходит при защите дипломного проекта, когда бывший студент предстает в новом качестве — в качестве инженера, геолога, врача, учителя, агронома и т. д.

При таком диалектическом подходе к процессу обучения студенты должны чувствовать, что их развитие с момента поступления в институт и его окончания (отрицания), идет по спирали.

И последнее. Для успешного обучения в вузе студентам необходимо хорошо разобраться во взаимосвязи законов диалектики, которая описана выше. Это поможет им еще успешнее разрешать встречающиеся противоречия и успешнее двигаться по пути своего развития.

Формированием диалектического мышления студентов автор занимается на всех видах занятий, а более конкретно — на лабораторных занятиях, поскольку в каждой лабораторной работе поставлены мировоззренческие вопросы и при защите выполненной работы каждый студент имеет возможность обсудить эти и другие вопросы с преподавателем.

Заключение

Итак, рассмотрено семь составляющих развивающего обучения:

1.      Усиление теоретической подготовки студентов.

2.      Индивидуализация аудиторных и домашних заданий.

3.      Исследовательская работа студентов.

4.      Изобретательская (творческая) деятельность студентов.

5.      Профессиональная ориентация решаемых задач.

6.      Элементы проблемного обучения.

7.      Формирование диалектического мышления.

Перечисленные действия преподавателей и студентов образуют единую взаимосвязанную технологическую цепочку развивающего обучения. Автор не только разработал эту цепочку, но реализовал ее созданием инновационно-дидактического комплекса [28] и воплощением всех его компонентов в жизнь (учебный процесс).

Существуют еще дополнительные составляющие развивающего обучения, например, привлечение студентов к техническому творчеству. Автор имеет опыт и в этом направлении. Так, кружком СНО при кафедре «Механика» в 2006 году было изготовлено порядка 80 учебных наглядных пособий, за что он был награжден Почетной грамотой университета. Кафедра пополнилась учебным оборудованием, а автор (с коллегами) подготовил и издал «Технический альбом» [29]. Автор широко пользуется и другим приемом: привлечением студентов к реферативной работе. Он выдает задания, например, по теме истории развития механики. Эти составляющие развивающего обучения, однако, носят добровольный характер и не охватывают всех обучающихся.

Важным показателем развивающего обучения является уровень его сложности. Это во многом зависит от умственной способности студентов, их физического и психического здоровья и желания добиваться высоких результатов в учебе, жизни, работе и своем положении в обществе.

Разработанная технология развивающего обучения является новой, поскольку автор интересовался наличием соответствующих учебно-методических комплексов у ведущих учебных заведений страны, но не обнаружил в них, например, заданий исследовательского характера, массового привлечения студентов к изобретательской деятельности и т. д.

Автор надеется, что разработанная технология развивающего обучения поможет коллегам других вузов, ученым педагогической науки, методистам и энтузиастам совершенствовать ее, дополнить другими составляющими и вернуть российскому образованию передовые позиции в мире.

 

Литература:

 

1.         Воронков И. М. Курс теоретической механики: Учебник для высших технических учебных заведений. Изд. шестое. — М.: Гос. изд-во технико-теоретич. литер., 1955. — 552 с.

2.         Тарг С. М. Краткий курс теоретической механики: Учеб. для втузов. — 10-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 416 с.

3.         Яблонский А. А. Курс теоретической механики: Учебник. 9-е изд., стер. / А. А. Яблонский, В. М. Никифорова. — СПб.: Издательство «Лань», 2002. — 768 с.

4.         Сборник заданий для курсовых работ по теоретической механике: Учебное пособие для технических вузов. — 7-е изд., исправленное / Под общей редакцией проф. А. А. Яблонского. — М.: Интеграл-Пресс, 2001. 384 с.

5.         Маркин Ю. С. Практический курс теоретической механики: Учеб. пособие. Части I и II. Статика, кинематика / Ю. С. Маркин, Ю. Я. Петрушенко. — Казань: Казан. гос. энерг. ун-т, 2008. — 320 с.

6.         Свидетельство № 29586 РФ. МКИ G 01 N 3/00. Устройство для исследования систем сходящихся сил / Ю. С. Маркин, Л. Г. Наумов, О. Ю. Маркин и др. Опубл. 20.05.2004. Бюл. № 14.

7.         Маркин Ю. С. Развивающее обучение теоретической механике [Текст] / Ю. С. Маркин // Педагогическое мастерство: материалы VI междунар. науч. конф. (г. Москва, июнь 2015 г.). — М.: Буки-Веди, 2015. — С. 182–188.

8.         Маркин Ю. С. Пособие по самостоятельному изучению теоретической механики. Часть I. Статика твердого тела / Маркин Ю. С., Петрушенко Ю. Я., Воздвиженская З. И. Учеб. пособие. — Казань: Казан. гос. ун-т, 2008. — 208 с.

9.         Маркин Ю. С. Пособие по самостоятельному изучению теоретической механики. Часть II. Кинематика точки и твердого тела / Маркин Ю. С., Петрушенко Ю. Я., Воздвиженская З. И. Учеб. пособие. — Казань: Казан. гос. ун-т, 2009. — 180 с.

10.     Ю. Маркин, З. Воздвиженская. Динамика. Самостоятельное изучение. — Saarbrucken, Germany: LAMBERT Academic Publishing. — 185 c.

11.     Маркин Ю. С. Тесты по теоретической механике. Часть I. Статика твердого тела: учеб пособие / Маркин Ю. С., Петрушенко Ю. Я. — Казань: Казан. гос. ун-т, 2011. — 298 с.

12.     Ю. Маркин. Статика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 373 c.

13.     Ю. Маркин. Кинематика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 296 c.

14.     Ю. Маркин, З. Воздвиженская. Динамика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 397 c.

15.     Маркин Ю. С. Задания к исследованию новых составных конструкций. Часть I. Статика твердого тела: учеб. пособие / Ю. С. Маркин. — Казань: Казан. гос. энерг. ун-т, 2013. — 92 с.

16.     Маркин Ю. С., Казанцева Н. С. Научно-исследовательская работа студентов первого курса по теоретической механике. Вестник Казанского государственного энергетического университета. № 2(17). 2013. С. 135–146.

17.     Ю. Маркин. Твердые тела с изменяемыми линейными параметрами. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 229 c.

18.     Ю. Маркин, О. Маркин. Инновации: в учебном процессе, сельском хозяйстве, промышленности. — Saarbrucken, Germany: «LAP LAMBERT Academic Publishing», 2012. — 395 с.

19.     Ю. Маркин. Новые механизмы. Составные и шарнирно-рычажные. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 308 c.

20.     Ю. Маркин. Новые механизмы. Шарнирно-рычажные, кулисные, кулачковые и другие. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 306 c.

21.     Ю. Маркин. Механизмы с изменяемыми линейными параметрами. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 367 c.

22.     Ю. Маркин, О. Маркин. Задачи. Профессионально-направленные и исследовательские. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 207 c.

23.     Культина Н. Ю. Как решать задачи по теоретической механике: Учебно-методическое пособие / Культина Н. Ю., Новиков В. В. — Нижний Новгород: Нижегородский госуниверситет, 2010. — 60 с.

24.     Лабораторный практикум по теоретической механике (с грифом) / Ю. С. Маркин, Л. Г. Наумов, О. Ю. Маркин, М. Г. Яруллин. Под ред. д.т.н., профессора Ю. С. Маркина. — Казань:: Казан. гос. энерг. ун-т, 2005. — 188 с.

25.     Лабораторный практикум по теории механизмов и машин. Часть 1. Исследование механизмов с учетом упругости звеньев (с грифом) / / Ю. С. Маркин, М. Г. Яруллин, О. Ю. Маркин, С. М. Яхин. Под ред. д.т.н., профессора Маркина Ю. С. — Казань: Казанск. гос. энерг. ун-т, 2006. — 199 с.

26.     Сельскохозяйственные машины вибрационного действия: Лабораторный практикум (с грифом) / Ю. С. Маркин, М. Г. Яруллин, О. Ю. Маркин / Под ред. д.т.н., проф. Маркина Ю. С. — Казань: Изд-во Казанск. ун-та, 2004. — 144 с.

27.     Педагогика и психология высшей школы / под. ред. М. В. Булановой-Топорковой: Учебное пособие. — Ростов н/Д: Феникс, 2002. — 544 с.

28.     Маркин Ю. С. Обновленный инновационно-дидактический комплекс по механике [Текст] / Ю. С. Маркин // Теория и практика образования в современном мире: материалы VII междунар. науч. конф. (г. Санкт — Петербург, июль 2015 г.). — СПб.: Свое издательство, 2015. С. 140–144.

29.     Маркин Ю. С. Наглядные учебные пособия по механике: Технический альбом / Ю. С. Маркин, Ю. Я. Петрушенко, О. Ю. Маркин. — Казань: Казан. гос. энерг. ун-т, 2007. — 104 с.