О реализации преемственности при обучении бакалавров физико-математического образования дискретной математике
Автор: Жмурова Ирина Юньевна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
международная научная конференция «Актуальные вопросы современной педагогики» (Уфа, июнь 2011)
Статья просмотрена: 223 раза
Библиографическое описание:
Жмурова, И. Ю. О реализации преемственности при обучении бакалавров физико-математического образования дискретной математике / И. Ю. Жмурова. — Текст : непосредственный // Актуальные вопросы современной педагогики : материалы I Междунар. науч. конф. (г. Уфа, июнь 2011 г.). — Уфа : Лето, 2011. — С. 102-105. — URL: https://moluch.ru/conf/ped/archive/18/815/ (дата обращения: 25.04.2024).
Переход высшего педагогико-математического образования на многоуровневую систему, четко определив ядро специальной математической подготовки студентов в виде государственных образовательных стандартов, расширил возможности вариативного компонента этой подготовки. Это позволило при проектировании как инвариантных дисциплин, так и курсов по выбору, уделять специальное внимание интеграционным связям отдельных математических дисциплин со всеми компонентами профессиональной подготовки будущего учителя математики, а также со всеми компонентами общечеловеческой культуры.
В реальном мире все системно и взаимосвязано, поэтому и знания, описывающие многообразие форм этого мира, должны быть системными. Овладение определенной системой знаний и адекватными ей видами деятельности являются и средством, и целью по отношению к развитию личности студента. Достаточно полный и систематизированный запас знаний об окружающем мире является важнейшим показателем развития личности и сформированности научного мировоззрения.
Такой подход способствует формированию целостных представлений о мире, картины мира как единого процесса. Интеграция знаний на основе интердисциплинарных и, особенно, интерблоковых связей позволяет восстановить на новом, более высоком уровне целостное видение проблем, процессов, явлений во всей полноте, многогранности, многоаспектности. Различные способы освоения мира (наука, искусство, техника и др.) дают возможность многомерного видения проблемы. Именно поэтому интеграция является сегодня определяющей тенденцией познавательного процесса. Интеграционные связи способствуют реализации всех функций обучения: образовательной, развивающей и воспитывающей, которые осуществляются во взаимосвязи и взаимозависимости. При этом средствами реализации таких связей могут быть как новые курсы по выбору, спроектированные на интегративной основе, так и базовые дисциплины, при обучении которым максимально актуализируется интеграционный компонент.
Система профессиональной подготовки бакалавров физико-математического образования включает в себя целый ряд разнообразных математических дисциплин. Все эти дисциплины читаются разными преподавателями, работающими на разных кафедрах. В результате у подавляющего большинства студентов отсутствует единый взгляд на математику, различные курсы воспринимаются в виде множества разрозненных теорий, зачастую никак не связанных между собой. Поэтому реализация внутриматематических интердисциплинарных связей – одна из важнейших задач профессиональной подготовки будущего учителя. По нашему мнению, курс «Основы дискретной математики», являющийся одним из первых математических курсов, обладает достаточно мощным интеграционным потенциалом.
При этом особенно остро встает вопрос об осуществлении преемственных связей между школой и вузом. Преемственность в содержании и методах обучения, максимальное использование ранее полученных знаний, их развитие и закрепление являются необходимым условием успешности обучения, особенно обучения математике. Поэтому курс основ дискретной математики, как и другие математические дисциплины, читаемые студентам-первокурсникам, является естественным продолжением и развитием школьного курса математики. Тем не менее, при переходе к этому курсу и в содержании, и в подходе к изучению материала, и в методике изложения происходит существенный качественный "скачок", который вызывает определенные затруднения у студентов. Эти трудности, естественно возникающие в процессе дидактической адаптации студентов-первокурсников к системе высшего педагогико-математического образования, объясняются как обилием нового материала, так и большей его абстрактностью и более высоким уровнем строгости изложения.
Одним из средств преодоления подобного рода затруднений мы видим реализацию преемственно-пропедевтической функции курса основ дискретной математики с помощью осуществления интердисциплинарных его связей со школьным курсом математики.
Рассматривая основные понятия дискретной математики, мы иллюстрируем их примерами элементарной математики, с помощью знакомого студентам материала переходим на более высокий уровень абстрактности, при изложении материала курса постепенно используем новые для студентов элементы языка и на последнем этапе переходим к изучению качественно нового материала. При этом максимально осуществляются интродисциплинарные связи курса. Так, например, при изучении элементов комбинаторики мы используем теоретико-множественные доказательства, бином Ньютона и полиномиальная формула доказываются не с помощью метода математической индукции (как в традиционном изложении), а исходя из комбинаторных соображений.
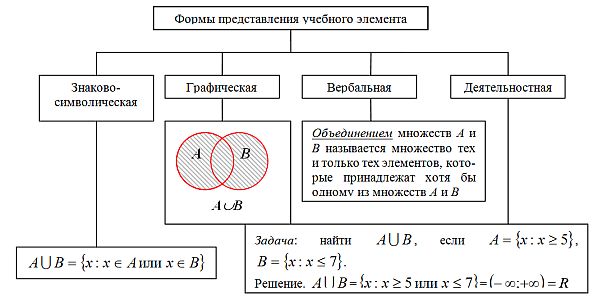
Далее, методической особенностью этого курса является последовательное осуществление взаимоперехода таких когнитивных сфер, как знаково-символическая, вербальная, графическая и деятельностная, моделируя учебные элементы в соответствующей учебной деятельности. Каждое новое понятие курса представлено следующим образом: вербальное определение, запись этого определения с помощью логико-речевой символики, графическая иллюстрация, решение соответствующей задачи. Так, в частности, на рис.1 и 2 изображены формы представления таких учебных элементов, как инъективное отображение и объединение множеств.
Рис. 1 Форма представления учебного элемента "объединение множеств"
Рис. 2 Форма представления учебного элемента "инъективное отображение"
Тем самым дискретная математика является своеобразным «мостом» между элементарной (школьной) математикой и вузовскими математическими дисциплинами.
Более того, сама дисциплина «Основы дискретной математики» является пропедевтической для изучения таких дисциплин, как алгебра, теория чисел, математический анализ, математическая логика и других, поэтому изучение дискретной математики в условиях реализации ее интеграционных связей помогает не только сделать более интересной саму эту дисциплину, но и повысить мотивацию обучения другим математическим курсам, тем самым осуществляется преемственность между дисциплинами математического блока в профессиональной подготовке будущего учителя математики.
Кроме того, еще одной из методических особенностей дискретной математики, реализующих преемственность между дисциплинами математического и информационного блоков, является использование в обучении информационных технологий. Глобальная информатизация общества значительно повлияла на изменение предмета и методов исследования разнообразных научных приложений. В ряде областей научного знания появились новые приемы, сформировались новые объекты изучения, возникли новые проблемы и задачи. Все это в определенной мере трансформировало сами науки, изменило их облик. Как отмечает академик В.А. Садовничий, "…с появлением компьютеров мир математики, безусловно, стал меняться. Изменяются не только математическое мышление, математические методы, но и научное мировоззрение в целом" [1].
При исследованиях в различных областях науки и техники компьютер можно использовать для наглядного представления результатов вычислений и обработки экспериментальных данных. В последние годы в теоретических исследованиях все шире применяются системы компьютерной алгебры. Еще одним примером является решение проблемы четырех красок – одного из приложений дискретной математики. В течение столетия эту проблему пытались решить многие математики, но решение удалось получить лишь после привлечения мощного компьютера. В процессе развития информатики шла интеграция этой научной дисциплины с целым рядом других наук. Для нас особый интерес представляет дискретная математика. В курсе основ дискретной математики компьютер используется как средство визуализации – для проведения компьютерных демонстраций; как средство вычислений – при решении рекуррентных соотношений и некоторых комбинаторных задач; как средство контроля – при проведении промежуточного контроля.
Нами используются компьютерные демонстрации к темам "Числа Фибоначчи", "Золотое сечение", изоморфизм графов, эйлеровы графы, планарные графы и др. Эти демонстрации позволяют осуществить визуализацию абстрактных понятий, повысить интерес к изучаемым вопросам, показать возможности использования материалов курса в будущей профессиональной деятельности.
Для решения рекуррентных соотношений и комбинаторных задач мы используем электронные таблицы – программу EXCEL, входящую в комплект программ Microsoft Office. С ее помощью можно вычислять значения целого ряда математических функций. Например, для решения рекуррентного соотношения необходимо найти корни характеристического уравнения; для вычисления числа сочетаний, размещений или перестановок при решении комбинаторных задач нужно вычислить значение факториала целого числа. Кроме того, электронные таблицы позволяют найти произвольное количество членов рекуррентной последовательности, проверив полученный результат. Мы не используем широко известные математические пакеты – такие, как MATLAB, MATEMATIKA, MAPLE и др., так как немногие студенты младших курсов владеют умением с ними работать. Возможности же программ комплекта Microsoft Office известны студентам как из школьного, так и вузовского курсов информатики.
Использование компьютера как средства контроля применяется при проведении промежуточного и рубежного контроля в форме теста.
Наконец, реализация интеграционных связей дискретной математики позволяет осуществить преемственность между дисциплинами математического и методического цикла. Для этого необходимо использовать возможности дискретной математики для подготовки будущего учителя к ведению в школе факультативных занятий и разработке элективных курсов. Практически все разделы курса основ дискретной математики могут быть построены таким образом, что соответствующие школьные факультативные или элективные курсы органически войдут в него начальной составной частью. Тем самым осуществляется преемственность между учебной деятельностью студента и профессиональной деятельностью учителя математики.
Таким образом, использование интеграционных связей дискретной математики в профессиональной подготовке бакалавра физико-математического образования позволяет максимально реализовать принцип преемственности.
-
- Литература:
Садовничий В.А. Математическое образование: настоящее и будущее // Доклад на Всероссийской конференции "Математика и общество. Математическое образование на рубеже веков". – Дубна, 2000
Похожие статьи
Некоторые аспекты эффективной подготовки будущих учителей...
Ключевые слова: эффективная подготовка, учитель математики, профессиональная деятельность, компетенция, математические дисциплины, школьная математика, взаимосвязь.
Профессиональная подготовка педагога...
В статье рассматривается актуальность профессиональной подготовки педагога; качества, которыми должен
организация педагогических курсов при учебных округах
Таким образом, в высшем педагогическом образовании наметилось два конструктивных подхода.
Содержание педагогической системы формирования...
Содержание педагогической системы формирования профессиональной подготовки будущих учителей информатики.
Ведущей формой организации учебного процесса в высшей школе является лекция.
Анализ психолого-педагогических условий профессиональной...
Анализ психолого-педагогических условий профессиональной подготовки будущих учителей математики на основании изучения представлений студентов о математическом образовании.
Особенности профессионально-педагогической подготовки...
Процесс преподавания математики на всех ступенях непрерывного математического образования во многом зависит от подготовки учителя математики. В связи с этим, в условиях развития новых педагогических и информационных технологий...
Элективный курс «Эйлеровы графы» как средство реализации...
Статья посвящена осуществлению интеграционных связей математики в профессиональной подготовке будущего учителя. Ключевые слова: интеграционные связи, проектирование, элективный курс.
Преподавание дисциплины «история информатики» для...
Прикладная математическая подготовка бакалавра менеджмента. Профессиональная подготовка бакалавра педагогического образования к трудовой деятельности.
О технологиях профессиональной подготовки будущих учителей в информационном обществе.
Инновационный метод обучения высшей математике студентов...
− математическое моделирование, которую можно проводить как компонент — самостоятельно в рамках ВУЗа или же в учебном плане дисциплины математика. − фундаментальный(базовый) курс высшей математики...
Некоторые подходы к включению будущих...
Организация исследовательской деятельности бакалавров — будущих педагогов-математиков, обучающихся по направлению подготовки 050100 — Педагогическое образование (профиль «Математическое образование»...
Похожие статьи
Некоторые аспекты эффективной подготовки будущих учителей...
Ключевые слова: эффективная подготовка, учитель математики, профессиональная деятельность, компетенция, математические дисциплины, школьная математика, взаимосвязь.
Профессиональная подготовка педагога...
В статье рассматривается актуальность профессиональной подготовки педагога; качества, которыми должен
организация педагогических курсов при учебных округах
Таким образом, в высшем педагогическом образовании наметилось два конструктивных подхода.
Содержание педагогической системы формирования...
Содержание педагогической системы формирования профессиональной подготовки будущих учителей информатики.
Ведущей формой организации учебного процесса в высшей школе является лекция.
Анализ психолого-педагогических условий профессиональной...
Анализ психолого-педагогических условий профессиональной подготовки будущих учителей математики на основании изучения представлений студентов о математическом образовании.
Особенности профессионально-педагогической подготовки...
Процесс преподавания математики на всех ступенях непрерывного математического образования во многом зависит от подготовки учителя математики. В связи с этим, в условиях развития новых педагогических и информационных технологий...
Элективный курс «Эйлеровы графы» как средство реализации...
Статья посвящена осуществлению интеграционных связей математики в профессиональной подготовке будущего учителя. Ключевые слова: интеграционные связи, проектирование, элективный курс.
Преподавание дисциплины «история информатики» для...
Прикладная математическая подготовка бакалавра менеджмента. Профессиональная подготовка бакалавра педагогического образования к трудовой деятельности.
О технологиях профессиональной подготовки будущих учителей в информационном обществе.
Инновационный метод обучения высшей математике студентов...
− математическое моделирование, которую можно проводить как компонент — самостоятельно в рамках ВУЗа или же в учебном плане дисциплины математика. − фундаментальный(базовый) курс высшей математики...
Некоторые подходы к включению будущих...
Организация исследовательской деятельности бакалавров — будущих педагогов-математиков, обучающихся по направлению подготовки 050100 — Педагогическое образование (профиль «Математическое образование»...