Развивающее обучение теоретической механике
Автор: Маркин Юрий Сергеевич
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
VI международная научная конференция «Педагогическое мастерство» (Москва, июнь 2015)
Дата публикации: 25.05.2015
Статья просмотрена: 1421 раз
Библиографическое описание:
Маркин, Ю. С. Развивающее обучение теоретической механике / Ю. С. Маркин. — Текст : непосредственный // Педагогическое мастерство : материалы VI Междунар. науч. конф. (г. Москва, июнь 2015 г.). — Москва : Буки-Веди, 2015. — С. 182-188. — URL: https://moluch.ru/conf/ped/archive/151/8214/ (дата обращения: 24.04.2024).
В статье рассмотрены приемы реализации развивающего обучения студентов первых — вторых курсов при изучении ими теоретической механики.
Ключевые слова: развивающее обучение, теоретическая механика
Keywords: developing training, theoretical Mechanics
Под развивающим обучением автор понимает создание условий для активно-деятельностной работы студентов над изучаемыми научными дисциплинами, в частности над теоретической механикой, с целью совершенствования их инженерной, профессионально-практической, творческой и мировоззренческой подготовки.
Прием первый. Индивидуализация обучения. Она заключается в том, что студенты получают индивидуальные задания: аудиторные (на практических занятиях, на занятиях по самоподготовке) или домашние (для изучения и решения задач в домашних условиях). Этот прием был реализован первоначально в пособии [1, 18], в котором материал раздела «Статика» разделен на 13 тем. Для каждой темы сформулированы вопросы для изучения, представлена литература, по которой студенты должны изучать требуемый материал и решать на эту тему задачи. Для каждой темы составлены контрольные карты с вопросами и задачами (по 30 карт к каждой теме). Ниже представлен пример одной из тем.
Раздел 1. ЗАНЯТИЕ № 1
Раздел: статика твердого тела.
Тема: история развития и основные понятия и определения механики.
Вопросы:
1. Механика — наука о механическом движении и взаимодействии материальных тел.
2. История развития механики.
3. Основные понятия и определения механики и статики.
4. Понятие силы и классификация сил.
5. Аксиомы статики.
Рекомендуемая литература
1. Маркин Ю. С., Петрушенко Ю. Я. Теоретическая механика, часть I, Статика твердого тела: Учеб. пособие. — 2-е изд., перераб. и доп. — Казань: КГЭУ, 2006. § 1.1, 1.2.
2. Тарг С. М. Краткий курс теоретической механики. — М.: Наука, 1972. § 18,19; § 42, 45.
3. Яблонский А. А. и Никифорова В. М. Курс теоретической механики. — М.: Издательство «Лань», 2002. § 19, 14–16.
Составить краткий конспект теоретических вопросов и решить задачи, приведенные в рекомендуемой литературе.
К каждой теме составлены контрольные карты, на вопросы которых должны отвечать студенты.
Примеры контрольных карт к занятию № 1
ЗАНЯТИЕ № 1
Статика Контрольная карта № 1
1. Дайте определение силы.
2. Сформулируйте первую аксиому статики.
3. Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.
4. Кто является основоположником статики?
ЗАНЯТИЕ № 1
Статика Контрольная карта № 2
1. Дайте определение системы сил.
2. Сформулируйте вторую аксиому статики.
3. Дайте определение абсолютно твердого тела.
4. Кто является основоположником теории механизмов и машин?
Пример контрольной карты по теме «Связи и реакции связей.
ЗАНЯТИЕ № 2
Статика Контрольная карта № 1
1. Дайте определение несвободного твердого тела.
2. Нанесите реакции связей (рис. 1).
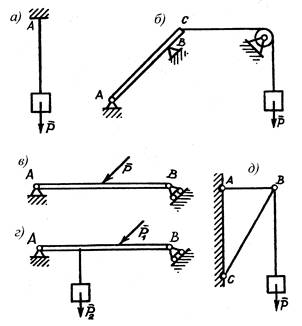
Рис. 1. Схемы вариантов заданий
Примеры контрольных карт к теме «Сложение сходящихся сил».
Сходящиеся силы можно складывать геометрически с помощью аксиомы о параллелограмме сил и построением силового многоугольника, а также аналитически. Это и предусмотрено в каждом индивидуальном задании.
ЗАНЯТИЕ № 3
Статика Контрольная карта № 1
1. Дайте определение системы сходящихся сил.
2. Сложите силы с помощью аксиомы о параллелограмме сил, векторным многоугольником и аналитически (рис. 2).
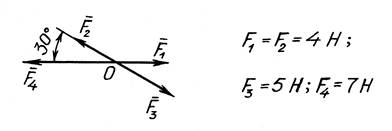
Рис. 2. Схема сходящейся системы сил
ЗАНЯТИЕ № 3
Статика Контрольная карта № 2
1. Как геометрически складываются две силы, приложенные к телу в одной точке под углом a?
2. Сложите силы с помощью аксиомы о параллелограмме сил, векторным многоугольником и аналитически (рис. 3).

Рис. 3. Схема сходящейся системы сил
И так в каждом из 13 занятий.
Аналогичные пособия составлены по кинематике [2, 8] (14 занятий) и по динамике [3, 5] (17 занятий).
Первоначально проверка студенческих ответов на вопросы контрольных карт производилась непосредственно преподавателем. Учитывая, что это очень трудоемкая работа, автор составил тесты по каждому разделу теоретической механики, например, [4, 4]. Со временем автор убедился в целесообразности преобразования тестов в форму вопросов и ответов и составил три новых пособия [5, 5; 6, 6; 7, 7].
Прием второй. Организация исследовательской работы студентов.
До теоретической механики автор преподавал теорию механизмов и машин (ТММ), в которой широко представлены вопросы исследований. Например, исследование изменения коэффициента полезного действия наклонной плоскости, исследование режимов движения роторов, исследование зубчатых зацеплений, исследование шарнирно-рычажных, кулисных и кулачковых механизмов, исследования, связанные с определением моментов инерции маховиков и т. д. Смена преподаваемой дисциплины в 2001 году долго смущала автора, поскольку в теоретической механике не оказалось такого большого количества исследовательских тем как в ТММ. Задания к расчетно-графическим работам автор выдавал по профессионально составленному и широко известному пособию [8, 7], но в котором задания (конструкции, устройства и механизмы) выполнены застывшими, т. е. с неизменяемыми линейными параметрами, не позволяющими организовывать исследовательскую работу студентов. И только летом 2011 года автору пришла идея преобразовать представленные в пособии [8, 23] задания. Первым заданием, подвергшимся преобразованию, явилось «Задание С.3. Определение реакций опор составной конструкции». Все 30 схем превратились в конструкции с изменяемыми линейными параметрами, чтобы снабжать студентов заданиями исследовательского характера. На новые конструкции были оформлены заявки на полезные модели в ФИПС и получены соответствующие патенты, по которым составлено пособие [9, 5]. В 2012 году такие задания были предложены одной из студенческих групп, с которыми автор занимался теоретической механикой. Перед студентами была поставлена задача — исследовать влияние размеров участков составных конструкций на величины реакций связей. Первые исследования студенты осуществляли вручную, например, [10, 135]. Исследования, выполняемые вручную, являются самыми полезными для студентов, поскольку все действия студентам приходится выполнять своими «пальчиками»: от изображения схем, нанесения реакций связей, составления уравнений равновесия и их решений, составления программы исследований, проведение исследований, построение графиков и до формулирования выводов о характере изменения реакций связей.
Несмотря на некоторое увеличение времени выполнения исследовательских заданий, к автору обратились студенты других групп как этого потока, так и групп лекционных потоков других институтов и факультетов. Автор в то время читал лекции на трех потоках, принадлежащих соответственно институту теплоэнергетики, институту электроэнергетики и электроники и факультету энергомашиностроения. Автор удовлетворил всех желающих. Ему было интересно знать, как будут выполнять исследования студенты разных институтов и факультетов. У него были некоторые сомнения об интеллектуальных возможностях студентов разных институтов и факультетов. В 2015 году он предложил задания исследовательского характера даже студентам заочного факультета, которые тоже все справились с индивидуальными задачами из книги [11, 23].
Ниже представлено исследование величин реакций связей от размеров участков твердого тела (ломаного стержня, рис. 4), выполненное студентом-заочником.
Дано: l1 = 3 м, P1 = 6 kH, P2 = 10 kH, M = 12 kHм.
Решение: поскольку левая часть стержня жестко заделана в неподвижное твердое тело (станину), реакцию связи в точке А студент разложил на составляющие 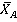 и
и 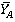 . Кроме того, в жесткой заделке (в точке А) возникает момент жесткой заделки
. Кроме того, в жесткой заделке (в точке А) возникает момент жесткой заделки 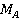 . Получилось, что к конструкции приложена плоская произвольная система сил.
. Получилось, что к конструкции приложена плоская произвольная система сил.
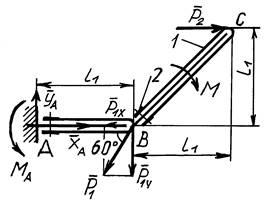
Рис. 4. Схема твердого тела с приложенными к нему силами и моментами
Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций действующих сил на каждую из координатных осей (х и у) равнялись нулю и алгебраическая сумма моментов сил относительно любого центра, лежащего в той же плоскости, тоже равнялась бы нулю.
Студент составил уравнения равновесия, решил их:
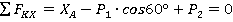 . (1)
. (1)
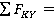
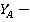
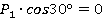 . (2)
. (2)
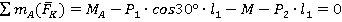 . (3)
. (3)
Из уравнения (1): 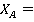
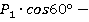
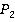 .
.
Из уравнения (2): 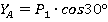 .
.
Из уравнения (3): 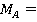
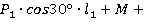
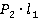 .
.
При вычислениях студент обнаружил, что
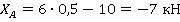 .
.
Знак «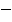 » говорит о том, что направление
» говорит о том, что направление 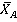 надо направить в противоположную сторону. Полученные результаты показывают, что при всех значениях l1 составляющая
надо направить в противоположную сторону. Полученные результаты показывают, что при всех значениях l1 составляющая 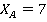 кН.
кН.
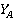 =
= 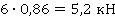 .
.
И этот результат подтверждает, что при всех значениях l1 составляющая 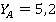 кН.
кН.
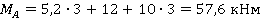 .
.
Все полученные вычислением результаты студент занес в таблицу 1.
Таблица 1
|
l1, м |
|
|
|
|
3 |
7 |
5,2 |
57,6 |
|
4 |
7 |
5,2 |
62,8 |
|
5 |
7 |
5,2 |
68 |
|
6 |
7 |
5,2 |
73 |
По табличным данным он построил графики исследуемых величин (рис.5).
Из построенного графика видно, что реакции связи 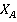 и
и 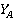 с увеличением участка АВ остаются постоянными, а момент
с увеличением участка АВ остаются постоянными, а момент 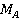 , возникающий в жесткой заделке, увеличивается.
, возникающий в жесткой заделке, увеличивается.
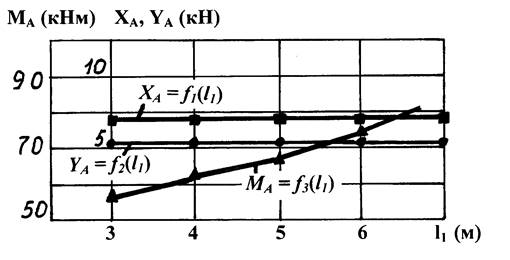
Рис. 5. Графики изменения реакций связей твердого тела
Автор постоянно совершенствует исследовательскую методику обучения студентов. Так, в 2013–2014 учебном году он работал со студентами Института экономики и информационных технологий по кафедре инженерной кибернетики. Студенты этого института (семь человек) составили 30 программ для исследования составных конструкций, описанных в пособии [9, 22]. Студенты, обучающиеся по прикладной математике, решали задачи по теоретической механике: вычерчивали схемы составных конструкций, наносили на них реакции связей, составляли уравнения равновесия, которые решали, а затем составляли соответствующие программы для исследования реакций связей этих конструкций. Все составленные программы зарегистрированы в ФИПСе. Таким образом, автор проверил возможность заниматься исследовательской работой студентов всех институтов и факультетов Казанского государственного энергетического университета.
Ниже (рис. 6) представлен пример выполнения исследований составной конструкции студентом Саяповым Артуром на компьютере с помощью составленной программы (группа ЭЭ-2–13).
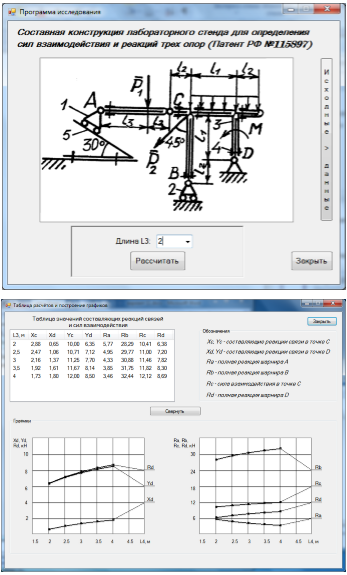
Рис. 6. Результаты исследования составной конструкции с помощью компьютера
Прием третий. Привлечение студентов к творческой работе. Руководя исследовательской работой студентов, автор заметил, что они хорошо владеют компьютерной графикой, и решил привлечь их к творческой работе. Они исследовали в это время составные конструкции, поэтому изучили их свойства, методы исследования, устройство и другие характеристики. В пособии [8, 28] представлены более сложные составные конструкции. Вот эти конструкции автор и решил предложить студентам совершенствовать: сначала задание С.4, названное как система трех тел, а затем задание С.9. Составные конструкции с внутренними односторонними связями. Студенты охотно согласились. Для этой работы был создан кружок студенческого научного общества (СНО) при кафедре «Механика», а затем при кафедре «Динамика и прочность машин». Каждую схему автор выдавал группе студентов. Каждый студент группы предлагал свою новую схему. Мы собирались во вне учебное время, обсуждали и выбирали наиболее совершенный вариант схемы. Иногда вносили коррективы. После этого составляли заявку на полезную модель и отсылали в ФИПС. При изучении кинематики студенты участвовали в совершенствовании шарнирно-рычажных механизмов (Задание К.4) [8, 80]. В 2012 году было подготовлено 100 заявок и получено столько же патентов Российской Федерации на полезные модели. Благодаря такой работе Казанский государственный энергетический университет среди вузов Республики Татарстан занял первое место. В течение 2013 и 2014 годов кружок СНО выдавал ежегодно также по 100 патентов, а автор разработал новую методику преподавания теоретической механики: «От научных исследований — к разработке учебного оборудования».
В связи с положительными результатами обучения студентов, автор продолжает разрабатывать задания исследовательского характера. За последнее время им разработаны схемы твердых тел [11, 35] и механизмы с изменяемыми линейными параметрами [12, 23], а также задания по следующим темам:
1. Детали и устройства с изменяемой геометрией.
2. Шарнирно-рычажные механизмы.
3. Стенды для исследования сложного движения точки.
4. Устройства для исследования относительного движения точки.
5. Устройства для исследования их принципом Даламбера.
Поскольку заданий исследовательского характера скопилось уже много, автор приступил к разработке справочника по таким механизмам.
Прием четвертый. Профессиональная ориентация решаемых задач. Проводя практические занятия по теоретической механике, автор заметил, что если задачи носят общий характер, то студенты несколько инертно относятся к их решению, но стоит представить им задачу, перекликающуюся по содержанию с их будущей профессиональной деятельностью, это их оживляет, они начинают проявлять интерес к задаче и решение задач проходит более интенсивно. Студенты задают вопросы, предлагают какие-то новые условия задачи, пытаются получить другие решения и т. д. Автор подготовил такой сборник задач, работая еще в сельскохозяйственных вузах, а опубликовать его [13, 10] удалось недавно. Интересуясь такой проблемой, автор обнаружил, что она волнует не только его, а многих преподавателей теоретической механики. Так, в Нижегородском государственном университете им. Н. И. Лобачевского провели специальное исследование [14, 3], в котором отметили, что при решении задач «включаются все мыслительные процессы: внимание, восприятие, память, воображение, мышление. В этом реализуется развивающая функция упражнений в решении задач».
Работа над созданием развивающего обучения идет по нескольким направлениям:
1. Развивающее обучение, прежде всего, охватывает систематическое развитие всех обучающихся (студентов).
2. Развивающее обучение должно вести к осознанию студентами процесса учения, т. е. к выработке потребности самостоятельного добывания знаний.
3. Развивающее обучение должно показывать студентам, что их обучение соответствует высокому уровню трудности.
4. Развивающее обучение должно предусматривать ведущую роль теоретических знаний.
5. И, наконец, развивающее обучение должно предполагать высокие темпы изучения различных материалов.
Вводя в учебный процесс элементы развивающего обучения, автор выбрал экспериментальную группу, над которой установил наблюдение. Его интересовали, прежде всего, результаты ее развития. В ней после первого семестра было 3 отличника и 7 человек имели пятерки и четверки, всего 10 человек. После выполнения исследований и участия в совершенствовании учебного оборудования во втором семестре стало 4 отличника и 9 — с пятерками и четверками, всего 13 человек. Успеваемость у этой группы постепенно росла, и в 6-м семестре было 6 отличников и 11 человек — с пятерками и четверками, всего 17 человек из 30 человек в группе. Такие же успехи были у группы и в 7-м семестре.
Группа заканчивает бакалавриат. Автора будет интересовать дальнейшее развитие группы. Сколько человек будет поступать в магистратуру, сколько человек окончат спецгруппу по целевому распределению и т. д.
Автор убедился в перспективности развивающего обучения, и обращается к коллегам других ВУЗов с просьбой — вскрыть и другие приемы создания развивающего обучения.
Литература:
1. Маркин Ю. С. Пособие по самостоятельному изучению теоретической механики. Часть I. Статика твердого тела / Маркин Ю. С., Петрушенко Ю. Я., Воздвиженская З. И. Учеб. пособие. — Казань: Казан. гос. ун-т, 2008. — 208 с.
2. Маркин Ю. С. Пособие по самостоятельному изучению теоретической механики. Часть II. Кинематика точки и твердого тела / Маркин Ю. С., Петрушенко Ю. Я., Воздвиженская З. И. Учеб. пособие. — Казань: Казан. гос. ун-т, 2009. — 180 с.
3. Ю. Маркин, З. Воздвиженская. Динамика. Самостоятельное изучение. — Saarbrucken, Germany: LAMBERT Academic Publishing. — 185 c.
4. Маркин Ю. С. Тесты по теоретической механике. Часть I. Статика твердого тела: учеб пособие / Маркин Ю. С., Петрушенко Ю. Я. — Казань: Казан. гос. ун-т, 2011. — 298 с.
5. Ю. Маркин. Статика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 373 c.
6. Ю. Маркин. Кинематика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 296 c.
7. Ю. Маркин, З. Воздвиженская. Динамика. Вопросы и ответы. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 397 c.
8. Сборник заданий для курсовых работ по теоретической механике: Учебное пособие для технических вузов. 7-е изд., исправленное. Под редакцией проф. А. А. Яблонского. — М.: Интеграл-Пресс, 2001. — 384 с.
9. Маркин Ю. С. Задания к исследованию новых составных конструкций. Часть I. Статика твердого тела. Учеб. пособие / Ю. С. Маркин. — Казань: Казан. гос. ун-т, 2013. — 92 с.
10. Маркин Ю. С., Казанцева Н. С. Научно-исследовательская работа студентов первого курса по теоретической механике. Вестник Казанского государственного энергетического университета. № 2(17). 2013. С. 135–146.
11. Ю. Маркин. Твердые тела с изменяемыми линейными параметрами. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 229 c.
12. Ю. Маркин. Механизмы с изменяемыми линейными параметрами. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2014. — 367 c.
13. Ю. Маркин, О. Маркин. Задачи. Профессионально-направленные и исследовательские. — Saarbrucken, Germany: «PALMARIUM Academic Publishing», 2013. — 207 c.
14. Культина Н. Ю. Как решать задачи по теоретической механике: Учебно-методическое пособие / Культина Н. Ю., Новиков В. В. — Нижний Новгород: Нижегородский госуниверситет, 2010. — 60 с.
Похожие статьи
Технология развивающего обучения в вузах | Статья в сборнике...
теоретическая механика, студент, автор, маятниковая рама, развивающее обучение, исследовательский характер, задание, твердое тело, работа, Контрольная карта.
Научно-исследовательская работа студентов...
На каждом уровне обучения необходимо развивать у студентов творческое мышление, исследовательские умения, без которых трудно как продолжать образование, так и реализовываться на рынке труда.
Обновленный инновационно-дидактический комплекс по механике
развивающее обучение, теоретическая механика, студент, пособие, автор, лабораторное оборудование, инновационно-дидактический комплекс, изобретательская работа, патент, лабораторный практикум.
Интеграция опыта по физике и математике с нацеленностью на...
Рис. 7. Балка (абсолютно твердое тело) под нагрузкой (пример системы параллельных сил).
Развивающее обучение теоретической механике. 3. Основные понятия и определения механики и статики. 4. Понятие силы и классификация сил.
Проблемы организации учебно-исследовательской деятельности...
Проблемы организации учебно-исследовательской деятельности студентов-бакалавров по дисциплинам «Техническая механика» и
Основные термины (генерируются автоматически): студент, задача, работа, проблемное обучение, дисциплина, учебный процесс...
Учебно-исследовательская работа студентов технологического...
самостоятельная работа, студент, самостоятельная работа студентов, учебный процесс, работа, задание, занятие, задача, начертательная геометрия, рейтинговая система обучения. Технология использования учебно-исследовательских задач...
Использование комплексных задач в процессе обучения...
теоретическая механика, студент, III, комплексное задание, система сил, тело системы, самостоятельная работа, плоская фигура, Произвольная плоская система, главный момент.
Методика проведения контроля знаний студентов по курсу...
Развивающее обучение теоретической механике. Раздел: статика твердого тела.
10. Маркин Ю. С., Казанцева Н. С. Научно-исследовательская работа студентов первого курса по теоретической механике.
Исследовательское обучение как средство формирования...
Главная особенность исследовательского обучения – активизировать учебную работу студентов, придав ей исследовательский, творческий характер и, таким образом, передать учащимся инициативу в организации познавательной деятельности.
Похожие статьи
Технология развивающего обучения в вузах | Статья в сборнике...
теоретическая механика, студент, автор, маятниковая рама, развивающее обучение, исследовательский характер, задание, твердое тело, работа, Контрольная карта.
Научно-исследовательская работа студентов...
На каждом уровне обучения необходимо развивать у студентов творческое мышление, исследовательские умения, без которых трудно как продолжать образование, так и реализовываться на рынке труда.
Обновленный инновационно-дидактический комплекс по механике
развивающее обучение, теоретическая механика, студент, пособие, автор, лабораторное оборудование, инновационно-дидактический комплекс, изобретательская работа, патент, лабораторный практикум.
Интеграция опыта по физике и математике с нацеленностью на...
Рис. 7. Балка (абсолютно твердое тело) под нагрузкой (пример системы параллельных сил).
Развивающее обучение теоретической механике. 3. Основные понятия и определения механики и статики. 4. Понятие силы и классификация сил.
Проблемы организации учебно-исследовательской деятельности...
Проблемы организации учебно-исследовательской деятельности студентов-бакалавров по дисциплинам «Техническая механика» и
Основные термины (генерируются автоматически): студент, задача, работа, проблемное обучение, дисциплина, учебный процесс...
Учебно-исследовательская работа студентов технологического...
самостоятельная работа, студент, самостоятельная работа студентов, учебный процесс, работа, задание, занятие, задача, начертательная геометрия, рейтинговая система обучения. Технология использования учебно-исследовательских задач...
Использование комплексных задач в процессе обучения...
теоретическая механика, студент, III, комплексное задание, система сил, тело системы, самостоятельная работа, плоская фигура, Произвольная плоская система, главный момент.
Методика проведения контроля знаний студентов по курсу...
Развивающее обучение теоретической механике. Раздел: статика твердого тела.
10. Маркин Ю. С., Казанцева Н. С. Научно-исследовательская работа студентов первого курса по теоретической механике.
Исследовательское обучение как средство формирования...
Главная особенность исследовательского обучения – активизировать учебную работу студентов, придав ей исследовательский, творческий характер и, таким образом, передать учащимся инициативу в организации познавательной деятельности.







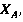 кН
кН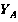 , кН
, кН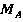 , кНм
, кНм



