Обучение учащихся использованию дополнительных построений в геометрических задачах
Авторы: Воистинова Гузель Хамитовна, Кулаков Александр Петрович
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
V международная научная конференция «Педагогическое мастерство» (Москва, ноябрь 2014)
Дата публикации: 07.11.2014
Статья просмотрена: 3495 раз
Библиографическое описание:
Воистинова, Г. Х. Обучение учащихся использованию дополнительных построений в геометрических задачах / Г. Х. Воистинова, А. П. Кулаков. — Текст : непосредственный // Педагогическое мастерство : материалы V Междунар. науч. конф. (г. Москва, ноябрь 2014 г.). — Москва : Буки-Веди, 2014. — С. 68-71. — URL: https://moluch.ru/conf/ped/archive/144/6587/ (дата обращения: 18.04.2024).
Статья посвящена проблеме обучения учащихся использованию дополнительных построений при решении геометрических задач, в частности использование плоскостного чертежа при решении стереометрических задач.
Ключевые слова: обучение решению геометрических задач, дополнительное построение, чертеж геометрической задачи.
При доказательстве теорем элементарной геометрии и решении геометрических задач часто используются дополнительные построения. Однако, в существующей научно-методической литературе вопросы, связанные с использованием дополнительных построений, методикой их применения, практически не рассматриваются.
Охарактеризуем кратко основные направления, которые можно выявить во всем многообразии подходов к изучению дополнительных построений.
К ним относятся:
1) Обучение эвристическим приемам решения задач и организация исследовательской деятельности при осуществлении поиска дополнительных построений.
2) Использование различных дополнительных построений, связанных с данной фигурой.
3) Использование дополнительных построений определённого вида при решении конкретных геометрических задач.
4) использование дополнительных построений (плоскостных чертежей и сечений) при решении стереометрических задач.
Среди работ первого направления можно выделить работы [1–4, 9], в которых авторы предлагают методику формирования приемов «анализ» и «синтез» при изучении различных тем курса математики средней школы. По мнению указанных авторов, часто встречаются задачи, при решении которых простой анализ свойств, установленных для фигур, попадающих под элементы задачи, не приводит к решению. Вот тогда вводятся «дополнительные элементы», а для этого, как правило, выполняются «дополнительные построения».
Однако увидеть нужное дополнительное построение могут далеко не все. В школьной практике часто наблюдаются случаи, когда учащиеся выполняют такие построения «вслепую». Нередко убедившись в бесплодности своих попыток, учащиеся отказываются от решения задачи. Создается видимость, будто успех в выборе дополнительных построений целиком зависит от случайных обстоятельств. Вместе с тем существуют достаточно типичные дополнительные построения, к выполнению которых учащихся (в подавляющем большинстве) можно подготовить, однако исследований этого вопроса очень мало. В тоже время, есть (и много) таких геометрических задач, где выполнение дополнительных построений это искусство, которым владеют лишь некоторые учащиеся». Именно тем, что это искусство, т. е. область, где очень трудно сформулировать точные и четкие предписания, объясняются трудности, связанные с выбором дополнительных построений при решении задач, трудности, заключающиеся в том, чтобы увидеть метод и выполнить дополнительные построения.
Из конкретных дополнительных построений в данных работах рассматриваются: проведение радиусов и хорд окружности, проведение средней линии вспомогательного треугольника, удвоение медиан треугольника. В некоторых случаях дополнительные линии не затрудняют учащихся, а в других — нагромождение линий (в том числе ненужных, проведенных поспешно) мешает найти правильный путь решения. Поэтому учителю следует обратить внимание школьников на роль хорошего чертежа при отыскании плана решения задачи.
Отметим, что основную роль здесь играет умение учителя организовать процесс поиска учащимися необходимого дополнительного построения.
К работам второго направления можно отнести работы Т. А. Ивановой [6] и И. Ф. Шарыгина [10], в которых авторы приводят цикл задач, обучающих различным приемам дополнительных построений, связанных с трапецией. Например, Т. И. Иванова выделяет следующие, наиболее часто встречающиеся построения: проведение высот трапеции; проведение через одну из вершин трапеции отрезка, параллельного одной из боковых сторон или одной из диагоналей; построение точки пересечения прямых, содержащих боковые стороны; проведение через середину одного из оснований отрезков, параллельных боковым сторонам.
Третье направление исследований характеризуется разрозненностью результатов, т. к. используемые авторами дополнительные построения в этом случае являются не столько объектом изучения, сколько методом изучения геометрических фактов.
В качестве примера можно привести работы [5, 7, 8]. Например, в работе Е. Ф. Даниловой [5], отмечается, что при отыскании пути решения иногда значительную роль играют вспомогательные построения, т. е. такие построения, относительно которых в условии задачи нет явных указаний, о целесообразности и необходимости которых учащийся должен догадываться. Очень важно, по ее мнению, чтобы учащиеся при этом руководствовались определёнными соображениями, а не рассчитывали на удачу, как, например, при решении следующих задач. Ю. Б. Мельников предлагает в своей работе [7, с. 180–198] совокупность дополнительных построений и правил анализа чертежа как компоненту метода решения геометрических задач на «вычисление», основанную на создании математической модели с системой отношений в виде системы уравнений и неравенств.
Если первые три направления еще как-то раскрыты в научно-методической литературе, то четвертое направление разработано очень слабо. Практически нет исследований, посвященных методике обучения учащихся построению планиметрических чертежей, позволяющих решать стереометрические задачи. В научно-методической литературе встречаются только исследования, посвященные построению сечений при решении стереометрических задач.
Рассмотрим стереометрическую задачу, решение которой упрощается введением планиметрического чертежа.
В усеченный конус, образующая которого наклонена под углом 45 градусов к нижнему основанию, вписан шар. Найти отношение величины боковой к поверхности усеченного конуса к величине поверхности шара.
Дано: шар вписан в усеченный конус, угол ВАМ=45˚ (рис.1).
Найти: 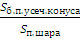 .
.
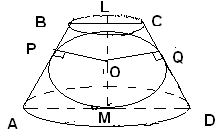
Рис. 1
Решение:
1. Проведем осевое сечение усеченного конуса. В сечении усеченного конуса получим равнобокую трапецию (т. к. вписан шар). Сечение шара — круг.
2. 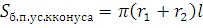 (1), где
(1), где 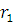 — радиус верхнего основания,
— радиус верхнего основания, 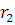 — радиус нижнего основания,
— радиус нижнего основания, 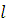 — образующая конуса.
— образующая конуса.
3. 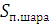 =
=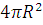 , (2), где R — радиус вписанного шара.
, (2), где R — радиус вписанного шара.
4. Рассмотрим данную задачу на плоскости (рис.2). Проведем радиусы из центра круга к сторонам трапеции и введем обозначения: BL=LC=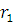 , AM=MD=
, AM=MD=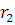 , OL=OM=OP=OQ=R, AB=CD=
, OL=OM=OP=OQ=R, AB=CD=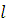 .
.
5. OL и ВС, ОР и АВ, ОМ и AD перпендикулярны, т. к. ОР, OL, ОМ — радиусы, а ВС, АВ и AD — касательные. По теореме о касательных к окружности, проведенных из одной точки, отрезки касательных будут равны. Таким образом, PB=BL=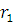 , а AP=AL=
, а AP=AL=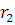 , значит образующая АВ=
, значит образующая АВ=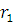 +
+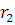 =
=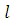 .
.
6. Подставим последнее равенство в формулу (1). Получим 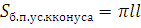 , или
, или 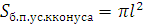 (3).
(3).
7. Проведем в сечении высоту BH, BH=LM (рис. 3). DABH прямоугольный с углами при вершинах А и В по 45 градусов. Значит DABH равнобедренный и AH=BH=2R.
8. Выразим AB=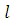 по теореме Пифагора через AH и BH, и подставим в (3).
по теореме Пифагора через AH и BH, и подставим в (3).
9. 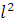 =
=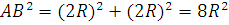 , тогда формула (3) примет вид
, тогда формула (3) примет вид 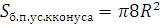 (4).
(4).
10. Найдем отношение площадей поверхностей. Выполнив деление (4) на (2), получим: 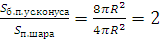 .
.
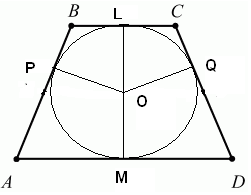
Рис. 2
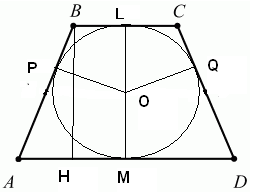
Рис. 3
Литература:
1. Воистинова Г. Х. Использование дополнительных построений при решении геометрических задач // Современные проблемы математического и физического образования в школе и вузе: Сб. трудов Всерос. научно-практ. конф., посв. 450-летию присоединения Башкортостана к России / Отв. ред. С. С. Салаватова. — Стерлитамак: Стерлитамак. гос. пед. академия, 2006. — С. 126–136.
2. Воистинова Г. Х. Основные приемы использования дополнительных построений при решении задач на построение // Этнокультурный компонент в образовательном процессе: теория и технология, передовой опыт»: Сборник трудов участников второго научно-мето-дического Всероссийского семинара 1–3 ноября 2013 г., г. Стерлитамак / Отв. ред. С. С. Салаватова. — Стерлитамак: Стерлитамакский филиал БашГУ, 2013. — С. 233–239.
3. Воистинова Г. Х. Задачи на построение как средство совершенствования приемов мышления студентов: Монография. — Стерлитамак: Стерлитамакский филиал БашГУ, 2013. — 176 с.
4. Гусев В. А. Психолого-педагогические основы обучения математике. — М.: Вербум, 2003. — 429 с.
5. Данилова Е. Ф. Как помочь учащимся находить путь к решению геометрических задач. — М.: Учпедгиз, 1961. — 143 с.
6. Иванова Т. А. Варьирование математических задач как средство развития интеллектуальных способностей учащихся // Развитие учащихся в процессе обучения математике: Межвуз. сборник науч. трудов. — Н. Новгород: НГПИ им. М. Горького, 1992–139 с.
7. Мельников Ю. Б. Математическое моделирование: структура, алгебра моделей, обучение построению математических моделей: Монография. — Екатеринбург: Уральское изд-во, 2004. — 384 с.
8. Раджабов М. Б. Формирование исследовательских умений и навыков учащихся неполной средней школы при изучении курса геометрии. — Душанбе, 1987. — 157 с.
9. Силаев Е. В. Использование дополнительных построений при решении геометрических задач. — М.: Прометей, 1994. — 116 с.
10. Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. — М.: Просвещение, 1989. — 252 с.
Ключевые слова
обучение решению геометрических задач, дополнительное построение, чертеж геометрической задачи., чертеж геометрической задачиПохожие статьи
Развитие творческого мышления учащихся при изучении понятий...
(Конус пересекается параллельной основанию плоскости по кругу).
1) Когда задача на построение сечения многогранника плоскостью считается решенной?
Обоснование прикладного характера науки геометрии в научном...
Наглядная геометрия | Статья в журнале «Школьная педагогика»
Построение геометрических фигур в масштабе. Решение задач практического характера.
Пирамида, усеченная пирамида.Объём пирамиды. Расчёт по формуле.
Тела вращения — 2 ч. Цилиндр, конус. Развертка и построение моделей.
Литература: Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия.
Противоречивые задачи в школьном курсе математики
Решение проблемно-поисковых задач на уроках математики как... При этом ответ к задаче для учащихся окажется особо неожиданным
В сечении усеченного конуса получим равнобокую трапецию (т. к. вписан шар). 7. Проведем в сечении высоту BH, BH=LM (рис. 3). DABH...
Решение задач с применением метода геометрических...
Научный журнал. Международные конференции. Тематические журналы.
Библиографическое описание: Устаджалилова Х. А., Махмудова О. Решение задач с применением метода геометрических преобразований с целью развития геометрических умений учащихся...
Роль задач с профессиональной направленностью в обучении...
Задача 2. Крыша имеет форму конуса. Высота крыши 2 м, диаметр 6 м. Сколько краски потребуется на ее окраску, если
Литература: И. И. Чичерин. «Общестроительные работы».
1) Когда задача на построение сечения многогранника плоскостью считается решенной?
Способ создания линии пересечения поверхностей вращения
Научный журнал. Международные конференции.
с пересекаемыми осями намного облегчает решение задачи.
Ключевые слова: окружность, метод, горизонталь, фронталь, профиль, ось, координата, проекция, плоскость, построение, модель, призма, пирамида, цилиндр, конус...
Методы эффективного использования законов перспективы при...
Основание конуса и диаметр цилиндра равны. Для построения падающей тени конуса, достаточно определить тень вершины TS.
Литература
Некоторые методические аспекты работы над пейзажем.
Pешение качественных задач один из приемов развития...
Литература.
Методические особенности обучения учащихся решению задач...
Метод решения качественных задач, состоит в построении логических связей, основанных на физических законах.
Метод кейсов в процессе обучения математике
Основой для создания задания для исследовательского кейса также может являться и содержательная олимпиадная задача.
Основные термины (генерируются автоматически): учащийся, ситуация, решение, Париж, исследовательский кейс, какая скорость...
Похожие статьи
Развитие творческого мышления учащихся при изучении понятий...
(Конус пересекается параллельной основанию плоскости по кругу).
1) Когда задача на построение сечения многогранника плоскостью считается решенной?
Обоснование прикладного характера науки геометрии в научном...
Наглядная геометрия | Статья в журнале «Школьная педагогика»
Построение геометрических фигур в масштабе. Решение задач практического характера.
Пирамида, усеченная пирамида.Объём пирамиды. Расчёт по формуле.
Тела вращения — 2 ч. Цилиндр, конус. Развертка и построение моделей.
Литература: Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия.
Противоречивые задачи в школьном курсе математики
Решение проблемно-поисковых задач на уроках математики как... При этом ответ к задаче для учащихся окажется особо неожиданным
В сечении усеченного конуса получим равнобокую трапецию (т. к. вписан шар). 7. Проведем в сечении высоту BH, BH=LM (рис. 3). DABH...
Решение задач с применением метода геометрических...
Научный журнал. Международные конференции. Тематические журналы.
Библиографическое описание: Устаджалилова Х. А., Махмудова О. Решение задач с применением метода геометрических преобразований с целью развития геометрических умений учащихся...
Роль задач с профессиональной направленностью в обучении...
Задача 2. Крыша имеет форму конуса. Высота крыши 2 м, диаметр 6 м. Сколько краски потребуется на ее окраску, если
Литература: И. И. Чичерин. «Общестроительные работы».
1) Когда задача на построение сечения многогранника плоскостью считается решенной?
Способ создания линии пересечения поверхностей вращения
Научный журнал. Международные конференции.
с пересекаемыми осями намного облегчает решение задачи.
Ключевые слова: окружность, метод, горизонталь, фронталь, профиль, ось, координата, проекция, плоскость, построение, модель, призма, пирамида, цилиндр, конус...
Методы эффективного использования законов перспективы при...
Основание конуса и диаметр цилиндра равны. Для построения падающей тени конуса, достаточно определить тень вершины TS.
Литература
Некоторые методические аспекты работы над пейзажем.
Pешение качественных задач один из приемов развития...
Литература.
Методические особенности обучения учащихся решению задач...
Метод решения качественных задач, состоит в построении логических связей, основанных на физических законах.
Метод кейсов в процессе обучения математике
Основой для создания задания для исследовательского кейса также может являться и содержательная олимпиадная задача.
Основные термины (генерируются автоматически): учащийся, ситуация, решение, Париж, исследовательский кейс, какая скорость...











