Когнитивно-визуальный подход к обучению математике как эффективное средство математического развития учащихся

Аннотация. В статье рассматривается одна из важных проблем в теории и методике обучения математике, связанная с учетом психофизиологических особенностей обучающихся при выборе технологии обучения, представлены примеры и приемы работы с учебным материалом, раскрывающие сущность когнитивно-визуального подхода к обучению математики.

Ключевые слова: визуальная среда обучения, когнитивно-визуальный подход к обучению, функциональная асимметрия полушарий головного мозга, образное мышление.

На современном этапе развития российского школьного образования большое значение приобретает его гуманистическая направленность. Одной из главных задач образования становится такая организация учебного процесса, которая направлена на развитие личности, предполагающее формирование у нее механизмов самовоспитания и самообучения через удовлетворение ее базовых потребностей: в психологически комфортных межличностных отношениях и социальном статусе, в реализации своего творческого потенциала, в познании в соответствии со своими индивидуальными когнитивными стратегиями.

Основные направления модернизации образования изложены в ФГОС (Стандарт). В основе Стандарта лежит системно-деятельностный подход, который обеспечиваетпостроение образовательного процесса с учетом индивидуальных, возрастных, психо-физиологических особенностей обучающихся, что, несомненно, инициирует новые возможности для построения более эффективного процесса предметного обучения.

Главными результатами обучения математике долгое время считались знание большого объема теоретического материала, умения и навыки в решении разнообразных математических задач. Однако, сейчас стало понятно, что при переносе полученных знаний в нестандартные ситуации, учащиеся испытывают значительные трудности, а порой они не в силах применить готовые схемы и алгоритмы для выхода из сложных ситуаций. Несоответствие между знанием большого массива учебной информации и умением его использовать в нестандартных ситуациях все больше и больше указывает на несостоятельность предметно-ориентированной парадигмы образования.

Педагогическая практика показывает, что в настоящее время противоречия между репродуктивными и развивающими способами обучения приобрели устойчиво-затяжной характер и привели к необходимости поиска и реализации нового подхода к методам и технологиям обучения.

Анализ школьной практики показывает, что современная система обучения математике построена на эксплуатации абстрактно-теоретического мышления, что в основе своей не согласуется с особенностями мышления значительной части учащихся. В этих условиях масштаб и эффективность образовательного процесса более высокого уровня лимитируются традиционными методиками обучения, абстрактным содержанием учебного материала в учебниках по математике, отсутствием опоры на образный компонент мыслительной деятельности.

Открытие в 1981 году американским неврологом Р. Сперри функциональной ассиметрии головного мозга привело к необходимости переоценки роли образного мышления в процессе обучения математике. Согласно современным представлениям межполушарная асимметрия – это различие полушарий по принципам организации контекстуальной связи между элементами информации, каковыми выступают слова и образы. За логико-вербальную, абстрактную переработку информации ответственны преимущественно функциональные системы левого полушария, за пространственно-образную, конкретную – правое полушарие.

Учитывая эти факторы, в образовательные стратегии следует инвестировать технологии обучения, реализующие, в первую очередь, возможности базисного, наглядно-образного компонента мыслительной деятельности, исходя из генетической первичности этого вида мышления. «Человеку изначально (по природе) была присуща высокая образность, которую нужно вернуть; это мощное биолого-эволюционное основание, необходимость для антропологической трансформации. С развитием же цивилизации человек стал запоминать не образ, а абстрактную информацию», – подчеркивает А.А Гостев [3, с. 31].

В.С. Ротенберг [7] отмечает, что мышление, лишенное элементов образности, рискует стать сухим, бесплодным, формальным. Обучение совсем не адресованное к образному мышлению, не только не способствует его развитию, но и, в конечном счете, подавляет его. Отсутствие опоры на образную сторону учебного материала не просто затрудняет обучение, а подчас придает ему мучительный характер, приводит к конфликту между образно мыслящим учеником и «сухой», скучной учебной работой.

Преимущество зрительного образа по сравнению с двигательными или слуховыми состоит в том, что он «позволяет одновременно выделять в модели-образе множество аспектов, мгновенно проникать в суть проблемы во всей ее сложности. В зрительном образе возможна фиксация различных теоретических связей и зависимостей (пространственных, структурных, функциональных, временных)» [4, с. 53].

Мышление зрительными образами, или «визуальное» мышление, рассматривается как сложный процесс преобразования зрительной информации. Это обеспечивается перцептивными действиями, дающими возможность создавать образы в соответствии с исходной наглядностью, оперировать ими, решать задачи на сравнение образов, их опознание, идентификацию, трансформацию.

Работы американского психолога Р. Арнхейма [1, 2] о роли визуального мышления в познавательной деятельности коренным образом изменили взгляд на традиционную наглядность, отдавая приоритет визуализации практически любого учебного материала.

Организация деятельности визуального мышления школьников в процессе обучения связана с конструированием визуальной учебной среды нового типа. Визуальной средой обучения Н.А. Резник [6] называет совокупность условий обучения, в которых акцент ставится на использование и развитие визуального (зрительно-наглядного) мышления. Эти условия предполагают целый спектр средств и приемов, позволяющих активизировать работу зрительной системы с целью получения продуктивных результатов.

К одним из основных требований, предъявляемых к созданию визуальной учебной среды, относится учет возможностей и индивидуальных особенностей обучаемого в восприятии учебной информации. В связи с этим, в содержание визуальной учебной среды следует включать те визуализированные объекты окружающей природы и культурно-предметного окружения, которые хорошо знакомы учащимся. Такой подход к формированию наглядной информации задает базовый ориентир и направлен на обоснование и понимание учащимися вводимых новых понятий, способствует росту мотивационной активности учащихся в процессе обучения. Л. М. Фридман отмечает: «Наглядность есть показатель простоты и понятности для данного человека того психического образа, который он создает в результате процессов восприятия, памяти, мышления и воображения»[8, с. 205].

Образовательная практика показывает, что одним из перспективных направлений в процессе обучения математике является применение когнитивно-визуального (зрительно-познавательного) (В. А. Далингер, О. О. Князева [5]) подхода, который базируется на оптимальном использовании резервов визуального мышления учащихся.

Применение этой технологии позволяет визуализировать широкий спектр учебной информации, способствует широкому и целенаправленному применению наглядности в процессе обучения, обеспечивает доступность знаний. Более того, «одним из достоинств когнитивно-визуального подхода является то, что он учитывает индивидуальные особенности учащихся и, в частности особенности левого и правого полушарий головного мозга», – отмечает В.А. Далингер [5, с. 6].

Оперирование образами в процессе познавательной деятельности позволяет установить своеобразную форму взаимодействия субъекта и объекта (иногда даже виртуального), что в конечном итоге приводит к созданию яркого и понятного образа этого объекта. Информация заключенная в наглядно фиксируемых образах носит вполне понятный и определенный смысл.

Проиллюстрируем вышесказанное с помощью следующих задач.

Задача1. Найти, чему равен квадрат четырехчленна (a+b+c+d).

Решение.

Нарисуем квадрат со стороной a+b+c+d (рис. 1)

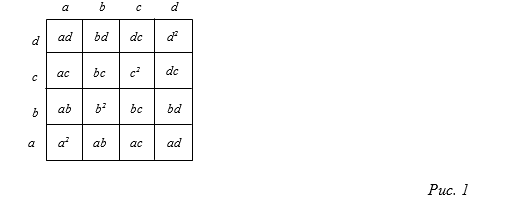
Считывая информацию с рисунка, получаем формулу:

(a+b+c+d)² = a² + b² + c² + d² + 2ab + 2ac +2ad + 2bc + 2bd + 2cd

Задача 2. Треугольная сетка (рис. 2) сделана из шнура, который может гореть. Огонь распространяется с одной и той же скоростью по всем направлениям (каждое звено сгорает за 1 минуту). Какие из отмеченных звеньев (AB, BC, DE, или AF) сетки сгорят последними, если поджечь сетку в точке O? За какое время они сгорят?

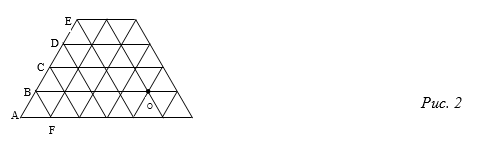
Решение.

Как видно из рисунка, огонь доберется до любой из точек B, C, D, E, F за 4 минуты. Следовательно, последними сгорят отрезки AB, AF, и произойдет это за 5 минут (отрезки DE, BC, CD сгорят за 4,5 минуты, потому что будут гореть с двух концов).

Трудно переоценить роль когнитивно-визуального подхода в изучении геометрии. Благодаря этой технологии у обучаемых развивается конструктивистское мышление и творческое воображение, формируется устойчивая положительная мотивация.

На рисунках 3, 4, 5, 6, приведены когнитивно-визуальные доказательства теоремы о площади трапеции.

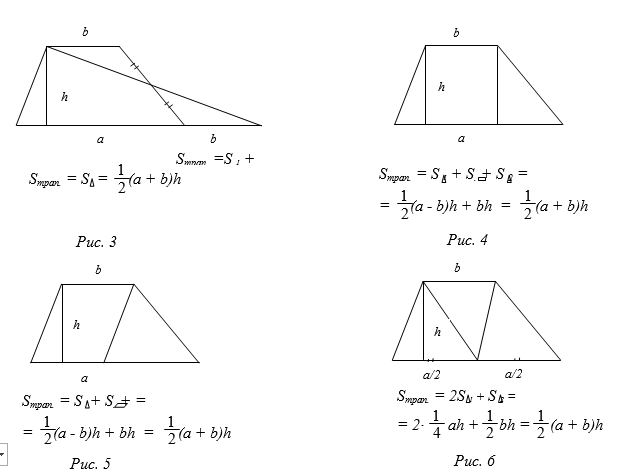
Разумеется, представленные варианты не исчерпывают все многообразие способов доказательства теоремы о площади трапеции.

Образовательная практика показывает, что использование наглядных образов в обучении может превратиться из вспомогательного приема обучения в ведущее, продуктивное методическое средство, способствующее математическому развитию учащихся. Язык образов является основным средством наглядности при изучении математики, позволяющий осознанно оперировать с понятиями и умозаключениями, закреплять и «оживлять» их в памяти.

Литература:

1.      Арнхейм, Р. Визуальное мышление. Хрестоматия по общей психологии. Психология мышления / Р.Арнхейм; под ред. Ю.Б. Гиппенрейтер, В.В Петухова. − М.: Изд-во МГУ, 1981. − С. 97− 107.

2.      Арнхейм, Р. Искусство и визуальное восприятие. − М.: Прогресс, 1974. − 392 с.

3.      Гостев А.А. Образная сфера человека / Рос. АН. Ин-т психологии. Всерос. н. – и. центр традиц.нар. медицины. – М., 1992. – 194 с.

4.       Гусев В.А. Психолого-педагогические основы обучения математике. − М.: Вербум-М 2003. – 429 с.

5.      Далингер В.А., Князева О.О. Когнитивно-визуальный подход к обучению математике: Учебное пособие / В.А. Далингер, О.О. Князева. − Омск: Изд-во ОмГПУ, 2004. – 344 с.

6.      Резник Н.А. Методические основы обучения математике в средней школе с использованием средств визуального мышления: автореф… д-ра пед.наук: 13.00.02 / Н.А. Резник − Москва, 1997. − 31 с.

7.      Ротенберг В.С., Бондаренко С.М. Мозг. Обучение. Здоровье: Кн. Для учителя. – М.: Просвещение, 1989. – 239 с.

8.      Фридман Л.М.Теоретические основы методики обучения математике: Учебное пособие. Изд. 2-е, испр. и доп. – М.: Едиториал УРСС, 2005. − 248 с.

.