Графы в Scilab
Автор: Моторина Екатерина Алексеевна
Рубрика: 12. Технические средства обучения
Опубликовано в
V международная научная конференция «Педагогическое мастерство» (Москва, ноябрь 2014)
Дата публикации: 01.11.2014
Статья просмотрена: 762 раза
Библиографическое описание:
Моторина, Е. А. Графы в Scilab / Е. А. Моторина. — Текст : непосредственный // Педагогическое мастерство : материалы V Междунар. науч. конф. (г. Москва, ноябрь 2014 г.). — Москва : Буки-Веди, 2014. — С. 284-287. — URL: https://moluch.ru/conf/ped/archive/144/6530/ (дата обращения: 16.04.2024).
В статье рассматриваются возможности использования математического программного обеспечения при решении задач теории графов. Рассматриваются некоторые аспекты представления графов в системе Scilab.
Ключевые слова: graph theory, Skilab, mathematical software, теория графов, математическое ПО.
Теория графов играет большую роль в подготовке специалистов в самых разных отраслях. Трудно представить себе специалиста, никогда не представлявшего ту или иную насущную задачу в виде графа. Причем решать графовые задачи зачастую приходится специалистам, не знакомым с основами теории графов. Поэтому многие задачи ими решаются неэффективно, или даже некорректно.
В последние годы теория графов стала одним из наиболее бурно развивающихся разделов математики. Это, прежде всего, связано с тем, что теория графов, родившаяся при решении головоломок и занимательных задач, стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Рождением теории графов можно считать 1736 год, когда Леонард Эйлер опубликовал решение задачи о кёнигсбергских мостах в трудах Петербуржской Академии наук. Можно предположить, что в этой задаче не впервые использовалось представление реалий графом, но впервые было проведено выделение графового метода представления как самостоятельного, имеющего собственную теоретическую ценность. Другой практической задачей, возникшей как популярная головоломка, стала задача о гамильтоновом цикле. Головоломка представляла собой додекаэдр в котором необходимо пройти все вершины графа. Эта задача и сейчас играет важную роль в планировании и носит название задачи коммивояжера (Traveling Salesman Problem — TSP). Задача, связанная с раскраской географической карты вылилась в задачу составления расписаний. Задача о раскладке графа на плоскости — в задачу о построении слоев печатных плат в электронике.
Из представленных примеров видно, что теория графов является одним из самых наглядных инструментов математики, использующих естественные принципы человеческого мышления и наглядного представления информации. В виде графов можно представлять, например, схемы дорог и коммуникаций, географические карты и молекулы химических соединений, связи между людьми, организациями, и многое другое. Это и привело к широкому использованию теории графов в физике и кибернетике, химии и биологии, экономике, статистике и других науках. Также важна роль теории графов в современном программировании и робототехнике.
Длительное время задачи теории графов решались вручную. С появлением же вычислительной техники для их решения стали использовать стандартные алгоритмические языки программирования. С повышением доступности вычислительных средств и широким распространением компьютеров появились математические пакеты, такие как Mathematica, MATLAB, Mathcad и Maple, позволяющие производить символьные вычисления. Наиболее широкое распространение для решения графовых задач получил пакет Maple, имеющий в своем составе специализированную библиотеку networks [1]. Небольшой состав команд библиотеки можно компенсировать, использую средства программирования Maple, позволяющие решать довольно сложные задачи — например, задачу коммивояжера, используя алгоритм муравьиных колоний. Вместе с тем, Maple имеет существенный недостаток — он довольно дорог, и большинство университетов, школ и отдельных пользователей не могут себе позволить приобретать его. К счастью, платной системе Maple есть бесплатная, свободно распространяемая система Scilab.
Система Scilab, как и Maple обладает подключаемым пакетом Metanet [2], позволяющим производить операции над графами и решать графовые задачи, а наличие в Scilab встроенного языка программирования дает возможность создавать программы, решающие довольно серьезные задачи теории графов.
Библиотека поддерживает работу как с ориентированными, так и с неориентированными графами. Для упрощения функционирования, все представления графов сводятся к орграфам (считается, что неорграф является частным случаем орграфа с двумя противоположно направленными дугами), и работа ведется с дугами. Каждый узел и каждая дуга имеет свой номер. При представлении графа обязательными являются 5 элементов структуры: имя графа (тип: строка); флаг, показывающий тип графа (1 — ориентированный, 0 — неориентированный); номера узлов или вершин; вектор (tail) заходящих в вершины дуг; вектор (head) исходящих к вершинам дуг.
Такие же элементы как имена вершин (node_name), их тип (node_type), координаты для отображения вершин (узлов) в окне (node_x, node_y), цвет узлов (node_color) и т. п. являются необязательными атрибутами. Для создания графа в системе Scilab используется функция make_graph с указанием обязательных атрибутов (например, g=make_graph(’foo’,1,4,[1 1 2 3],[2 3 1 3]);) — см. рис. 1. Граф, заданный командой, представлен на рис. 2.
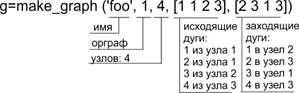
Рис. 1. Пример представления графа в системе Scilab
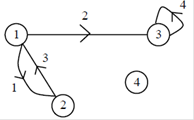
Рис. 2. Вид графа из примера
Для многих операция Scilab использует представление графов списком смежности. Он использует три массива: lp — массив указателей, ls — массив узлов графа и la — массив дуг графа. Если граф имеет n вершин и m дуг, то массивы будут иметь следующие размеры: lp — размер n+1, ls и la — размер m. При таком способе представления легко определить последователей тех или иных узлов. Каждый узел i имеет lp(i+1)-lp(i) узлов-последователей с номерами от ls(lp(i)) до ls(lp(i+1)-1), а соединяющие их дуги имеют номера от la(lp(i)) до la(lp(i+1)-1). Для рассмотренного выше примера список смежности представлен на рис. 3
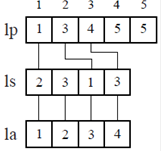
Рис. 3. Список смежности графа из примера
Кроме того, возможно и представление графов матрицами инцидентности и смежности. Функции, работающие с этими матрицами, носят названия graph_2_mat и mat_2_graph.
Графы можно сохранять в виде ASCII-файлов, имеющих расширение .graph. Структура такого файла:
GRAPH TYPE (0 = UNDIRECTED, 1 = DIRECTED), DEFAULTS
NODE DIAMETER, NODE BORDER, first line continuing ARC WIDTH, HILITED ARC WIDTH, FONTSIZE):
<one line with above values>
NUMBER OF ARCS:
<one line with the number of arcs>
NUMBER OF NODES:
<one line with the number of nodes>
****************************************
DESCRIPTION OF ARCS:
ARC NAME, TAIL NODE NAME, HEAD NODE NAME, COLOR, WIDTH, HIWIDTH, FONTSIZE COST, MIN CAP, CAP, MAX CAP, LENGTH, Q WEIGHT,
Q ORIGIN, WEIGHT
<one blank line>
<two lines for each arc>
****************************************
DESCRIPTION OF NODES:
NODE NAME, POSSIBLE TYPE (1 = SINK, 2 = SOURCE)
X, Y, COLOR, DIAMETER, BORDER, FONTSIZE DEMAND
<one blank line>
<three lines for each node>
Причем для неориентированного графа, ARC заменяется EDGE. Кроме того, значения NODE DIAMETER, NODE BORDER, ARC WIDTH, HILITED ARC WIDTH и FONTSIZE для графа, COLOR, WIDTH, HIWIDTH и FONTSIZE для ребер, и POSSIBLE TYPE, COLOR, DIAMETER, BORDER и FONTSIZE для узлов могут не использоваться или быть равными нулю.
Для загрузки графа из файла следует выполнить команду load_graf. Например, если использовать имя переменной g для считываемого графа:
g=load_graph(‘foo');
или полностью с расширением:
g=load_graph('foo.graph');
Чтобы сохранить граф, следует использовать функцию save graph. Ее первый аргумент — список графов, второй — имя или путь к файлу графа; Если путь является именем каталога, то имя графа используется в качестве имени файла. Например, следующая команда сохраняет граф в граф файла foo.graph:
save_graph(g,’foo.graph’);
Самым простым способом визуализации графов является его построение в графическом окне Scilab, для сего можно использовать функцию plot_graph. Однако при использовании этой функции с графом не получится выполнять никаких действий. Если требуется интерактивная модификация графа, лучше использовать Metanet windows.
Пакет Metanet [2] включает в себя обширный инструментарий по работе с графами и вычислению отдельных их характеристик. Среди этих операций — добавление и удаление ребер (дуг) и вершин (узлов), объединение графов, определение компонент связности, фундаментальных циклов и многие другие. Наличие в Scilab собственной системы программирования позволяет решать многие довольно сложные графовые задачи, используя функции модуля Metanet.
Система Scilab является хорошей альтернативой математическому пакету Maple при решении задач теории графов.
Литература:
1. Кирсанов М. Н. Графы в Maple. Задачи, алгоритмы, программы. — М.: ФИЗМАТЛИТ, 2007. — 168 с. — ISBN 978–5-9221–0745–7
2. Claude Gomez, Maurice Goursat. Metanet User’s Guide and Tutorial http://people.bridgewater.edu/~rschneid/Archive/SciLab/metanet.pdf
Ключевые слова
теория графов, Теория графов, Skilab, Математическое программное обеспечение, математическое ПО., graph theory, mathematical software, математическое ПОПохожие статьи
Методы определения объектов на изображении | Статья в журнале...
Выделенные края могут быть двух типов: независящие и зависящие от точки зрения. Независящие границы отображают такие свойства, как цвет и форма поверхности.
for (int i = 0; i < img.size().width; i++) {.
The choice of feed circuit of modernized hydrostatic bearing of internal...
A mobile node on conventional hydrostatic bearing with multithreaded accomplice will have
3. The power supply system with throttle regulator diaphragm type.
where a — coefficient of discharge; — size of the input of the throttle; , — diameter of the throttle; — density of the fluid; — width adjustable...
Acidity and Concentrations of Aluminum in Atmospheric Deposition in...
The snow samples were taken at the maximal point of snow cover (April), using a 1-m long polyethylene tube with internal diameter of 14.5-cm.
They are Passive methods, Active methods and also interactive methods. This type of interactive method requires to study teaching material on the theme...
Похожие статьи
Методы определения объектов на изображении | Статья в журнале...
Выделенные края могут быть двух типов: независящие и зависящие от точки зрения. Независящие границы отображают такие свойства, как цвет и форма поверхности.
for (int i = 0; i < img.size().width; i++) {.
The choice of feed circuit of modernized hydrostatic bearing of internal...
A mobile node on conventional hydrostatic bearing with multithreaded accomplice will have
3. The power supply system with throttle regulator diaphragm type.
where a — coefficient of discharge; — size of the input of the throttle; , — diameter of the throttle; — density of the fluid; — width adjustable...
Acidity and Concentrations of Aluminum in Atmospheric Deposition in...
The snow samples were taken at the maximal point of snow cover (April), using a 1-m long polyethylene tube with internal diameter of 14.5-cm.
They are Passive methods, Active methods and also interactive methods. This type of interactive method requires to study teaching material on the theme...











