Математическое моделирование комплексных экономических процессов

Сегодня экономическая теория рассматривает достаточно сложные проблемы экономики на различных уровнях. Очевидно, что рассмотрение столь сложных вопросов требует применения многочисленных методов исследования. С каждым годом применение математического моделирования приобретает все большее значение. Во многом, это можно объяснить тем, что математические модели представляют собой некую основу экономических объектов. Математическое моделирование включает в себя построение математических моделей экономических объектов, методы решения и анализ полученных результатов. В итоге очевидно, что сегодня математическое моделирование актуально как никогда, особенно, в экономической сфере.

Ключевые слова: математическое моделирование, экономика, методы исследования, развитие, анализ результатов.

Today, the economic theory considers a rather complicated problems of the economy at different levels. It is obvious that the consideration of such complex issues requires the use of numerous methods. Every year the use of mathematical modeling is becoming increasingly important. Largely, this can be explained by the fact that mathematical models are a kind of basis of economic interest. Mathematical modeling involves the construction of mathematical models of economic objects, methods, solutions and analysis of the obtained results. In the end, it is obvious that mathematical modeling is more relevant than ever, especially in the economic sphere.

Keywords: mathematical modeling, Economics, research methods, development, analysis of results.

Моделирование как метод научного познания применялось еще в глубокой древности. Шло время, и оно постепенно стало применяться в новых областях научных познаний. И, именно, моделирование пришло в архитектуру и строительство, не обойдя стороной физику, химию и общественные науки. Однако, безусловно, нельзя сравнивать методологию моделирования древнего и современного миров. Но, несмотря, на большое количество различий, у моделирования разных времен есть одна общая черта. Во все времена моделирование рассматривалось как универсальный метод научного познания.

Сегодняшний современный мир, невозможно представить без экономики. А экономическая сфера, в свою очередь, невозможна и без моделирования. Поскольку, моделирование выступает одним из основных методов, применяющихся при принятии стратегически важных решений.

1.      Сущность математического моделирования

Для начала дадим определение моделированию. Само по себе моделирование представляет собой некий специфический способ познания, при применении которого характерные черты одной системы воспроизводятся в другой системе.

Из приведённого выше определения можно сделать вывод о том, что моделирование будет включать в себя как минимум две системы. Одна из которых будет являться исследуемой, также ее можно назвать исследуемым объектом. Второй же системой будет являться построенная нами модель. Однако, поскольку мы все-таки используем математические методы, то построенную модель следует называть системой. Отсюда и получаются две системы. Главной особенностью моделирования выступает тот факт, что этот метод познания является опосредованным. Иными словами, данный метод подразумевает использование объектов-заместителей. Модель же в таком методе является своеобразным инструментом познания, который стоит между исследователем и познаваемым объектом, то есть, получается, что именно с помощью модели происходит изучение мира (или объекта исследования). Именно из этой особенности метода следуют специфические (иногда даже не стандартные) формы использования категорий и методов познания. Здесь имеется в виду абстракция, аналогия и применение гипотез.

Необходимость использования метода моделирования очевидна. Определяющим критерием выступает тот факт, что многие объекты или проблемные аспекты (практически большинство) нельзя исследовать непосредственно «в лоб». Некоторые из них и вовсе не поддаются исследованию или даже если они поддаются исследованию, то оно требует слишком много времени и средств (а, ведь, во многих случаях решения нужно принимать в короткие сроки, особенно это характерно экономической сфере).

Моделирование как процесс включает три основных элемента:

-          субъект (исследователь);

-          объект исследования;

-          модель, которая опосредует отношения познающего субъекта и познаваемого объекта.

2.      Общая схема математического моделирования

Очевидно, что если рассматривать моделирование как процесс, то оно должно включать в себя определенные этапы.

Первый этап — экономический объект.

На данном этапе происходит выбор экономического объекта и происходит формулировка цели исследования. Отметим, что такие изучаемые объекты могут различаться по природе и по назначению. То есть они могут быть экономическими, социальными и так далее, в зависимости от сферы, в которой проводится исследование.

Второй этап — экономическая модель.

Очевидно, что для дальнейшего изучения явлений их необходимо описать. То есть создать модель. В нашем случае моделирование экономическое, а значит и создаваемая модель тоже будет экономической. Примерами экономической модели могут служить различные модели. Например, модель равновесия на рынке.

Построение любой экономической модели будет начинаться с выявления существенных и несущественных (второстепенных) факторов. Первый шаг будет именно таким так как процесс упрощения исходного явления лежит в основе любого научного исследования. Однако, при этом, законченная модель должна описывать широкий спектр особенностей функционирования модели.

Естественно, что все экономические модели делятся на две больших группы. Первая — микроэкономические модели, вторая группа — макроэкономические модели. Первая группа моделей занимает большую часть экономической теории, поскольку такие модели описывают структурные и функциональные составляющие экономики. Также в них отражены количественные соотношения вышеназванных составляющих. Вторая группа моделей (макроэкономические модели) описывает экономику в целом. Также модели второй группы связывают между собой показатели. Например, финансовые или материальные.

Третий этап — свойства среды.

На данном этапе рассматриваются свойства среды. Очевидно, что количество информации и ее полнота об элементах исследуемого объекта (модели) определяет полноту самой экономической модели. Отмечу, что информация может быть теоретическая, а может и носить эмпирический характер. Важно, только чтобы на данном этапе было точно сформированы и определены свойства изучаемой экономической среды.

Четвертый этап — математическая модель.

Итак, при математическом моделировании, мы имеем дело не с конкретным явлением, а с его теоретической «копией». Такой «копией» будет являться математическая модель, построенная в математической форме, и отражающая главные закономерности изучаемого явления. Отмечу, что математическая модель должна быть четко сформирована и содержать в себе все характеристики изучаемого явления. В противном случае, построенная нами модель не сможет дать ответы на поставленные в исследование вопросы. На практике проблемы с построением модели возникают не часто. И, как правило, построенные модели отражают в себе всю необходимую информацию. Добиться данного факта помогает процесс избавления от несущественных черт. Напротив, наиболее важные характеристики (для будущей модели) записывают в виде уравнений.

Здесь же применяются линейные методы решения, содержащие сумму различных частных решений поставленной задачи. Однако, сегодня наибольшей степенью распространённости обладают нелинейные явления в экономике. Очевидно, что такие объекты являются гораздо более сложными для исследования. Более того, такие модели часто меняют поведение не по определенным закономерностям, а скачкообразно, что сильно усложняет их изучение, и, особенно, прогнозирование. Основными методами, применяемым для таких объектов, являются численные методы.

Пятый этап — алгоритм решения.

Очевидно, что создание математической модели является всего лишь первым шагом. Следующим шагом идет изучение ее поведение. Иначе говоря, решить входящие в модель уравнения. Для этого используются числительные методы или как их еще называют вычислительные алгоритмы. Данные алгоритмы позволяют с достаточно высокой точностью получить приближенные решения довольно сложных задач.

Шестой этап — программная реализация.

Очевидно, что на данном этапе будет применяться компьютер. А именно, при его помощи, на одном из выбранных компьютерных языков, будет составляться программа. Данная программа и реализует выбранные в предыдущем пункте алгоритм решения.

Седьмой этап — завершающий.

На данном этапе будет проводиться анализ полученных результатов. Также результаты могут быть сопоставлены с их теоретическими прогнозами. Далее делаются выводы и, если требуется, прогноз.

Итак, в результате математического моделирования происходит видоизменение модели. Более того, создаются так называемые «эталонные модели». Итогом моделирования являются четкие количественные и практические рекомендации по модели.

На представленном ниже рисунке наглядно отражены этапы математического моделирования.

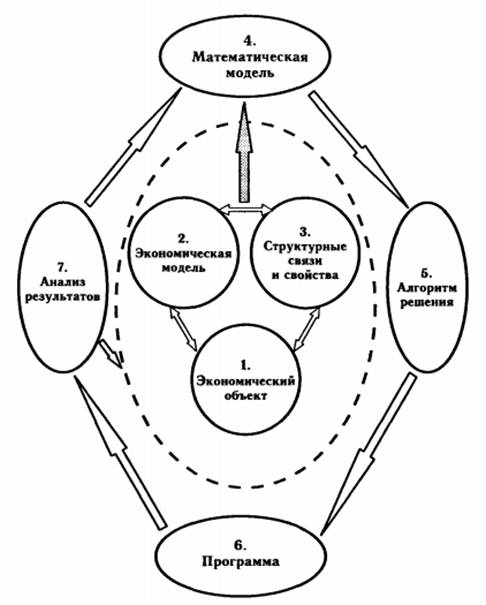
Рис. 1. Этапы математического моделирования

3.      Экономические модели

Для начала дадим определение экономической модели. Экономическую модель можно определить, как модель, основанную на экономической теории [2]. Как правило, экономическая теория описывает устойчивые связи между переменными. Рассмотрю пример из теории потребления. Возьмём простейшую форму зависимости потребления в период 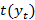 от дохода (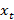). Предположим, что потребление будет пропорционально доходу и будет реагировать на его изменение моментально, то есть реакция проявляется в тот же период. Тогда верно следующее:

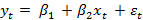                                                                                                   [1.1]

Где величина 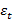 — случайная ошибка (отклонение).

Рассмотрим значение величины 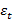 в уравнение [1.1], которая выражает случайную ошибку. Итак, несмотря на то, что в данном уравнении доход является наиболее значимым фактором, который формирует потребление, одного знания величины данного фактора недостаточно для точного определения потребления. Поскольку имеются другие различные факторы, которые не учитываются в модели, однако, их воздействие напрямую приводит к отклонениям от основной зависимости, то именно величина  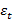позволит учесть их воздействие.

Далее перейдём к рассмотрению одной из основных моделей эконометрики. Основная процедура экономического оценивания параметров этой модели — метод наименьших квадратов (МНК). Отметим сразу, что значительная часть эконометрики посвящена адаптации этой модели к реальной жизни. Итак, пусть процесс, который приводит значения наблюдаемой переменной 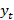 является суммой линейной комбинации 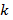объясняющих переменных  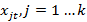и случайного отклонения :

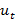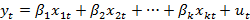
где 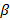 — неизвестны.

Как известно, основная задача эконометрики заключается в получении «оптимальных» оценок неизвестных параметров зависимости. Тогда, имея определенный массив наблюдений можно перейти от соотношений к матричной форме:

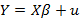
Где

Тогда получается, что Y является векторов наблюдаемых значений зависимой (или объясняемой) переменной размерности 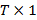; X является матрицей наблюдений, которые объясняют переменные («регрессоры») размерности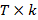;  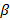является вектором неизвестных коэффициентов размерности 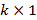; u является вектором ненаблюдаемых случайных отклонений (регрессионных ошибок) размерности .

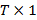Рассматривая классическую регрессионную модель, можно отметить, что в ней присутствует ряд допущений, которые позволяют установить свойства оценок коэффициентов. А именно:

1)        известно, что вcе случайные отклонения имеют нулевые математические ожидания и одинаковые дисперсии, также они являются взаимно некоррелированными, то есть:

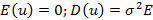
2)        Объясняющие переменные не случайные и получается, что они не зависят от случайных отклонений;

3)        Объясняющие переменные линейно независимые.

4.      Проверка адекватности моделей

Как уже отмечалось ранее, экономические процессы — это достаточно сложная для изучения вещь. Кроме того, имеется ряд особенностей, которые также затрудняют построение моделей. Однако, сложность построения модели — не единственная проблема. Ведь после построения модели, ее необходимо проверить на адекватность.

Если обратиться к естественным наукам, то здесь, факт совпадения результатов исследования с наблюдаемыми фактами является достаточным условием истинности. То есть, получается, что категория «практика» совпадает с категорией «действительность». Что касается экономики, то здесь такой принцип может применяться только к простым моделям. Такие модели просто описывают действительность или анализируют прошлое развитие.

Однако, главная задача экономической науки состоит в том, чтобы разработать научные методы планирования и управления экономикой. Именно исходя из это задачи выходит, что наиболее распространенным типом математических моделей экономики являются модели управляемых и регулируемых экономических процессов. Отмечу, что именно такие модели используются для преобразования экономической действительности. Они называются нормативными. Особенность моделей такого рода состоит в том, они, зачастую, «конкурируют» с другими моделями, несмотря на то, что последние уже нашли практическое применение. Еще более ситуация усложняется, когда, речь идет о верификации моделей долгосрочного прогнозирования и планирования. Ведь очевидно, что нельзя 10–15 лет пассивно ожидать наступления событий, чтобы проверить правильность предпосылок модели.

Несмотря на изложенные выше «отягощающие обстоятельства» важнейший критерий адекватности моделей остается неизменным. Им является соответствие модели фактам и тенденциям реальной экономической жизни. Отмечу, что, в тоже время, этот же критерий определяет направления совершенствования моделей. Процесс исправления ошибок, допущенных в модели, может развиваться только по одному алгоритму. А именно, следует провести всеобъемлющий анализ выявленных расхождений между действительностью и моделью. Далее необходимо сопоставить результаты по модели с результатами, полученными иными методами.

Еще одна важная роль в проверке моделей принадлежит логическому анализу, включая средства самого математического моделирования. Сюда входят, например, такие приемы как: проверка истинности статистических гипотез о связях между параметрами и переменными модели, доказательство существования решения в модели и другие. В целом, если оценивать проблему адекватности моделей, то можно сказать, что сегодняшняя экономика — это совокупность сложнейших процессов. Вполне естественно, что модели достаточно быстро становится не в состоянии отвечать все новым и новым параметрам. Однако, на мой взгляд, очевидно, что наличие определенной комплексной методики верификации моделей позволит решить сложившуюся проблему.

5.         Особенности применения метода математического моделирования в экономике

Сегодня очевидно, что экономика и математика — это две сложные науки, чье слияние, естественно, является сложным процессом со своими особенностями.

Большая доля затруднений в применении методов математического моделирования к сложным экономическим процессам вызвана тем фактом, что большинство объектов, которые изучает экономическая наука, являются не чем иным, как сложными системами.

Вернусь к определению системы. Под системой понимают совокупность элементов, которые находятся во взаимодействии и образуют некую целостность, единство. Здесь хотелось бы обратить внимание на то, что важным свойством любой системы является эмерджентность. То есть наличие таких свойств, которые не будут присущи ни одному из элементов по отдельности. Здесь же возникает и еще одна особенность применения математического моделирования к экономическим процессам. Дело в том, что при изучении систем недостаточно пользоваться методом разделения их на элементы (с последующим изучением этих элементов в отдельности). Ведь, очевидно, что почти не существует экономических объектов, которые можно было бы рассматривать как отдельные (в данном случае внесистемные) элементы.

Следующая особенность связана со сложностью системы. Я имею в виду, что сложность системы, как правило, определяется количеством входящих в нее элементов, связями между этими элементами, и взаимоотношениями между системой и средой. Из чего видно, что экономика страны является очень сложной системой (так как обладает всеми вышеназванными признаками). Иногда даже сложность экономики рассматривалась как причина невозможности ее моделирования или даже как причина невозможности изучения ее средствами математики. Однако, на мой взгляд, такая точка зрения неверна, поскольку я полагаю, что моделировать можно объект практически любой природы и практически любой сложности. Более того именно сложные объекты представляют наибольший интерес для моделирования, потому, что именно в данном случае моделирование может дать результаты, которые нельзя получить другими способами исследования.

Безусловно, наличие потенциальной возможности математического моделирования любых экономических объектов и процессов не означает, что она будет успешна осуществлена. Однако, на мой взгляд, современный уровень экономических и математических знаний, имеющейся конкретной информации и вычислительной техники позволят как никогда ранее осуществлять моделирование любой сложности. Хотя, конечно, всегда будут существовать некоторые проблемы, не поддающиеся математическому моделированию, или поддающиеся ему не с той степенью эффективности. И, пожалуй, этот фактор будет решающим в процессе развития и расширения области математического моделирования экономических процессов.

В заключение хотелось бы отметить, что сегодня область применения компьютерного моделирования для изучения и прогнозирования процессов, протекающих в социально-политической сфере, достаточно широка.

Сегодня математическое моделирование сложных экономических процессов решает ряд комплексных задач, таких как: выявление реальных структурных элементов среды, которые оказывают наибольшее влияние на развитие экономической и политической ситуации в стране, и соответственно, в мире; оценка возможных вариантов развития событий и, соответственно, оценка уровня риска в результате предполагаемых действий субъектов экономики или даже политики властей; прогнозирование результатов применения различных экономических мер и инструментов; а также оценка текущего уровня экономического развития региона, страны, мира.

Более того, математическое моделирование экономических процессов позволяет углубиться в количественный анализ экономических проблем. А этот факт, в свою очередь, позволяет принимать совершенно новые стратегические решения, которые способны сильно изменить экономическую ситуацию как в стране, так и в целом мире.

Кроме этого, математическое моделирование экономических процессов совсем не является сложной наукой, как может показаться на первый взгляд. Объясним почему. Дело в том, что у каждого человека есть своя модель окружающего мира. И, даже решение бытовых задач требует моделирования. Приведём пример. Допустим, индивид решил сходить в кафе или ресторан поесть. В таком случае, он должен принять целый ряд решений. А именно, индивид решает в каком конкретном месте и какое конкретное блюдо он хотел бы съесть, далее он обдумывает маршрут, потом он проверяет свою платежеспособность, и, наконец, берет собой определенную сумму денег и отправляется в путь. Очевидно, что мы специально не задумываемся, когда совершаем описанные выше действия. Однако, по факту, ряд этих действий и есть моделирование. Таким образом, выходит, что моделирование (в том числе и экономическое) присутствует не только в научной сфере нашей жизни.

Из сказанного выше можно сделать вывод, о том, что сегодня невозможно представить экономику (как столь сложную систему) без применения математического моделирования, а значит, область его применения будет только расширяться и способствовать все новым и новым исследованиям, открытиям и, как следствие, выводам и решениям.

Литература:

1.         Мажукин В. И. — М.: Флинта: Московский гуманитарный университет, «Математическое моделирование в экономике», Учебное пособие, 2004. — 232с.

2.         Грачева М. В., Фадеева Ю. Н., Черемных Ю. Н. — М.: ЮНИТИ-ДАНА, «Моделирование экономических процессов», Учебник, 2005. — 351с.

3.         Бывшев В. А. Эконометрика: Учебное пособие.– М.: «Финансы и статистика», 2008. — 480 с.;

4.         Магнус Я. Р. Эконометрика: Начальный курс: Учебное пособие/ Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий. — М.: Дело, 2005. — 503с;