Сегодня эконометрика является важной частью экономической теории. Пришло понимание того, что без построения эконометрических моделей невозможно проводить современный качественный микро- и макроэкономический анализ. Известно, что эконометрика сочетает в себе применение математических методов к статистическим данным и использование информационных технологий с целью автоматизации, обеспечения сложных расчетов и моделирования.
Серьезное влияние на совершенствование компьютерных алгоритмов и программного обеспечения в целом оказывают возрастающие в объеме информационные потоки, подвергаемые анализу. С этим связано появление ряда инструментов и технологий, таких как нереляционные масштабируемые базы данных, получившие обозначение NoSQL, программное обеспечение Hadoop, предназначенное для распределения задач по обработке больших данных (Big Data) по кластерам из сотен и тысяч узлов, модель MapReduce [1] и т. д.
В статье пойдет речь об использовании языка программирования и программной среды R, являющихся де-факто стандартом в области статистических вычислений. От других продуктов для статистической обработки данных, таких как Stata, SAS, SPSS Statistics или STATISTICA R выгодно отличается лицензией GNU GPL, подразумевающей свободное распространение, кроссплатформенностью и гибкостью — помимо осуществления стандартных вычислений существует возможность строить картограммы, создавать интерактивные веб-приложения и проводить тестирования [3]. Кроме этого, R позволяет максимально эффективно использовать вычислительные мощности ЭВМ — вычислительная среда адаптирована для работы на высокопроизводительных кластерах и в многоядерных системах. Эти преимущества способствуют популяризации R в научной среде, а сформировавшееся сообщество позволяет оперативно получать техническую поддержку и находить ответы на возникающие вопросы.
Основной целью эконометрики является модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, выявленными в экономической теории. Взаимосвязь между переменными величинами может быть описана разными способами. Так, например, коэффициенты корреляции отражают тот факт, что изменчивость одного признака зависит от изменчивости другого, а использование регрессионной модели позволяет выразить эту зависимость в виде функции.
Для того чтобы ознакомиться с основными возможностями R в области эконометрического моделирования, предлагается решить практическую задачу. Проведем анализ зависимости спроса на некоторый товар от его цены.
Таблица 1
Часть исходных статистических данных
|
Цена товара, тыс. р. |
2.4 |
2.6 |
3.2 |
3.3 |
3.5 |
3.4 |
3.4 |
3.8 |
... |
|
Кол-во проданных единиц товара в среднем за месяц, шт. |
3292 |
3201 |
2769 |
2708 |
2596 |
2600 |
2627 |
2766 |
... |
Загрузим табличные данные из текстового файла в текущее рабочее пространство командой read.table. Здесь и далее предполагается, что пользователь работает в RStudio в режиме скрипта, либо последовательно вводит команды в консоль.
> data <- read.table("D:\\data.txt", TRUE)
Первым параметром указывается абсолютный или относительный путь к файлу с данными. Затем — флаг, указывающий на то, что первой строкой (данные в файле отформатированы по столбцам) идут названия объектов. Здесь следует обратить внимание на некоторые особенности языка:
- R чувствителен к регистру — data и Data являются двумя разными объектами;
- В именах объектов традиционно не используют символ подчеркивания «_», поэтому в названиях функций часто можно встретить символ точки ««.;
- Операторами присваивания являются «<-» и «->»;
- Получить справку о команде можно добавив «?» перед ее названием.
Расчитаем далее коэффициент Пирсона корреляции спроса (Y), являющегося зависимой переменной, и цены (X) — независимой переменной или предиктора.
> cor(data$X, data$Y)
[1] -0.9791896
Предположительно, X и Y имеют обратную линейную связь. Проверим коэффициент корреляции на значимость. При данном уровне значимости P = 0.05 имеем нулевую гипотезу H0: r = 0 о равенстве нулю коэффициента корреляции и альтернативную гипотезу H1: r ≠ 0. Для проверки нулевой гипотезы используют величину (1), имеющую распределение Стьюдента с n-2 степенями свободы. Определив критическое значение, принимаем решение о принятии или отклонении гипотезы H0.
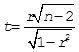(1)
> cor.test(data$X, data$Y)
...
t = -25.5307, df = 28, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9901587 -0.9562632
> abs(qt(0.05/2,6)) # критическое значение распределения для P = 0.05
[1] 2.446912
Поскольку в данном случае | t | > tкрит, то отвергаем нулевую гипотезу и делаем вывод о значимости коэффициента корреляции (в отчете также сообщаются границы его доверительного интервала). Можно строить модель линейной регрессии.
Используем простейшую модель y = β0 + β1x. Чтобы найти коэффициенты β0 и β1 задействуем функцию lm, принимающую в качестве обязательного аргумента формулу, описывающую выбранную регрессионную модель. Синтаксис формул представлен в Таблице 2.
Таблица 2
Синтаксис формул для команды lm
|
Модель |
Формула |
|
y = β0 + β1x |
y ~ x |
|
y = β1x |
y ~ 0 + x |
|
y = β0 + β1x + β2x2 |
y ~ x + I(x^2) |
|
y = β0 + β1x1 + β2x2 |
y ~ x1 + x2 |
|
y = β0 + β1x1x2 |
y ~ x1: x2 |
|
y = β0 + β1x1 + β2x2 + β3x1x2 |
y ~ x1 * x2 |
> lm(data$Y ~ data$X)
...
Coefficients:
(Intercept) data$X
5818 -957
Следующие выводы можно сделать учитывая найденные коэффициенты:
- если цена вырастет на 1 тыс. р., то спрос уменьшится в среднем на 957 шт.;
- если цена снизится до 0, то спрос составит в среднем 5818 шт.
Построим диаграмму рассеяния и график регрессии по найденным коэффициентам используя функции plot и abline.
> plot(data$X, data$Y, xlab="Цена, тыс. р.", ylab="Спрос, шт.")
> abline(lm(data$Y ~ data$X))
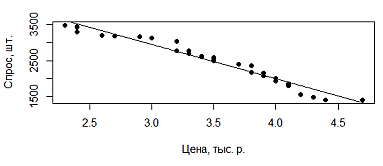
Рис. 1. Диаграмма рассеяния и линейная регрессия
Следующим шагом необходимо проверить на значимость полученное уравнение регрессии и отдельные его коэффициенты. Воспользуемся функцией summary, чтобы получить сводку результатов работы lm.
> summary(lm(data$Y ~ data$X))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5818.40 132.06 44.06 <2e-16 ***
data$X -957.00 37.48 -25.53 <2e-16 ***
...
Multiple R-squared: 0.9588, Adjusted R-squared: 0.9573
F-statistic: 651.8 on 1 and 28 DF, p-value: < 2.2e-16
Как и при проверке коэффициента корреляции R вычисляет величину t и степень значимости коэффициентов уравнения. В данном случае делаем вывод о значимости обоих коэффициентов. Коэффициент детерминации (R-squared) показывает, в какой мере изменение прогнозируемого параметра обусловлено изменением предикторов (изменение спроса на 95 % обусловлено изменением цены). Наконец, последняя строка сводки говорит об адекватности выбранной модели в целом — проверяется значимость всего уравнения с помощью критерия Фишера.
Стоит сказать, что в статье рассмотрен лишь ограниченный набор инструментов, доступных пользователю-эконометристу в среде R, в целом возможности языка гораздо шире. Более того, пакеты расширения, создаваемые независимыми разработчиками по всему миру, в значительной степени расширяют функционал R охватывают все больше аспектов статистической обработки данных. С их помощью решаются задачи, возникающие не только в эконометрике и финансовом анализе, но и в генетике и молекулярной биологии, экологии и геологии, медицине и фармацевтике. Значительная часть европейских и американских университетов в последние годы активно переходят к использованию R в учебной и научно-исследовательской деятельности вместо дорогостоящих коммерческих разработок [5].
Литература:
1. Varian H. R. Big Data: New Tricks for Econometrics // Journal of Economic Perspectives. 2014. Vol. 28(2).
2. Красильников Д. Е. Программное обеспечение эконометрического исследования // Вестник Нижегородского университета им. Н. И. Лобачевского. 2011. N 3(2). С. 231–238.
3. Smart F. Why use R? Five reasons. [Электронный ресурс] // URL: http://www.econometricsbysimulation.com/2014/03/why-use-r-five-reasons.html (дата обращения: 23.11.2014).
4. Шишкин В. А. Программное обеспечение экономических расчётов. Применение пакетов прикладных программ. [Электронный ресурс] // Пермь, 2014. URL: http://vsh1791.ru/texts/soft.pdf (дата обращения: 23.11.2014).
5. Статистический анализ данных в системе R: учебное пособие. / Буховец А. Г., Москалев П. В., Богатова В. П., Бирючинская Т. Я.; под ред. Буховца А. Г. Воронеж: Изд-во Воронежского государственного аграрного университета им. К. Д. Глинки, 2010.
