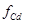Коэффициенты активности растворяющейся фазы гетерогенного сплава в условиях локальной вольтамперометрии
Авторы: Мощенская Елена Юрьевна, Слепушкин Вячеслав Васильевич, Рублинецкая Юлия Вячеславовна, Кашкаров Борис Игоревич
Рубрика: 3. Физическая химия
Опубликовано в
Дата публикации: 17.06.2015
Статья просмотрена: 142 раза
Библиографическое описание:
Мощенская, Е. Ю. Коэффициенты активности растворяющейся фазы гетерогенного сплава в условиях локальной вольтамперометрии / Е. Ю. Мощенская, В. В. Слепушкин, Ю. В. Рублинецкая, Б. И. Кашкаров. — Текст : непосредственный // Современная химия: Успехи и достижения : материалы I Междунар. науч. конф. (г. Санкт-Петербург, июль 2015 г.). — Санкт-Петербург : Свое издательство, 2015. — С. 29-35. — URL: https://moluch.ru/conf/chem/archive/122/8320/ (дата обращения: 18.04.2024).
Представлены новые выражения для коэффициентов активности растворяющейся фазы и градуировочных характеристик i=f(С) в условиях локальной вольтамперометрии (ЛВА), явившиеся развитием предыдущих исследований процесса анодного растворения гетерогенных сплавов
Ключевые слова:локальная вольтамперометрия, коэффициенты активности, активность, анодное растворение гетерогенных сплавов, градуировочные характеристики, парциальные токи.
Определение коэффициентов активности фазы гетерогенного сплава ранее [1–5] выполнялось по следующему уравнению:
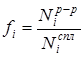 ; (1)
; (1)
где Nip-p- молярная доля компонента в растворе (находится из гибридной вольтамперной кривой, на третьей стадии поляризации [5]), Niспл — молярная доля компонента в сплаве (заведомо известная величина). Способ отличается достаточной трудоёмкостью и длительностью осуществления.
Чтобы уравнение для парциальных токов растворения фаз двухкомпонентного гетерогенного сплава (А-В) [5] соответствовало реальным зависимостям парциального тока растворения от состава, в него необходимо ввести коэффициент активности (fi) компонента:
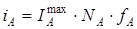 и
и 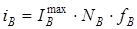 (2)
(2)
где NA, NВ — молярная доля компонентов в сплаве; IAmax, IВmax — максимальный ток растворения чистых компонентов.
Нами предложено для коэффициента активности следующее выражение:
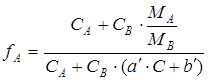 (3)
(3)
где MA, MB — молекулярные массы компонентов, г/моль; СА, СВ — содержание компонента в сплаве, %масс; 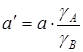 ;
; 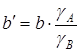 ; γА, γВ — плотность компонентов, г/см3; a и b — эмпирические постоянные. В уравнении (3) при СA→100 —
; γА, γВ — плотность компонентов, г/см3; a и b — эмпирические постоянные. В уравнении (3) при СA→100 — 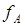 →1, а при CA→0 —
→1, а при CA→0 — 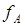 →
→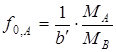 , то есть к постоянной величине — коэффициенту активности компонента при бесконечно малой концентрации (
, то есть к постоянной величине — коэффициенту активности компонента при бесконечно малой концентрации (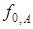 ). Физический смысл эмпирической постоянной b становится ясным:
). Физический смысл эмпирической постоянной b становится ясным:
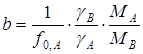 (4)
(4)
Кроме того, очевидно, что коэффициенты активности компонентов можно рассчитать из соотношения (2), используя экспериментальные данные по токам растворения фаз сплава [5]:
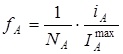 и
и 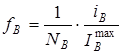 (5)
(5)
Также очевидно, что значения коэффициентов активности компонентов, найденные по уравнениям (1), (3) и (5) для эвтектических сплавов Cd-Bi, Sn-Bi и Cd-Sn должны совпадать — рис. 1–2, табл. 1–2.
Зная коэффициенты активности можно рассчитать активность (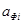 ) растворяющейся фазы:
) растворяющейся фазы:
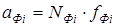 (6)
(6)
Из рис. 1 и табл. 1 очевидно, что гибридный способ ЛЭА [5] для системы сплавов Cd-Bi дает заниженные результаты по значениям активности и коэффициентам активности кадмия.
В то же время активность и коэффициенты активности кадмия в системе Cd-Sn, рассчитанные по уравнениям (1) и (5) хорошо совпадают. Следовательно, можно сделать вывод о том, что более надежные результаты дают уравнения (5) и (6) соответственно.
На основании вышеизложенного, можно предложить новые уравнения градуировочной кривой в локальной вольтамперометрии гетерогенных сплавов. Для двухкомпонентной системы А-В:
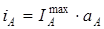 и
и 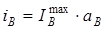 (7)
(7)
Или с учетом выведенного ранее [5, 6] уравнения:
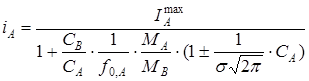 (8)
(8)
где σ — параметр характеризующий распределение фаз в матрице сплава.
Очевидно, что уравнение (8) не содержит эмпирических постоянных a и b, то есть более корректно описывает градуировочную кривую i=f(С).
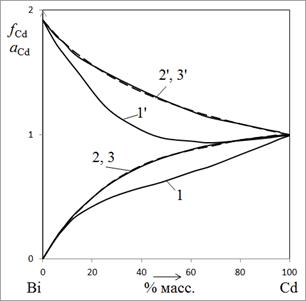
Рис. 1. Активность (1, 2, 3) и коэффициенты активности (1ˊ, 2ˊ, 3ˊ) Cd в матрице сплавов Cd-Bi при его растворении в 1 М NaClO4 в условиях локальной вольтамперометрии — ур. (1), (3) и (5) соответственно
Таблица 1
Коэффициенты активности кадмия в матрице сплавов кадмий-висмут при его растворении в 1 М NaClO4в условиях локальной вольтамперометрии МCd=112,41 г/моль; МBi=208,98 г/моль; γCd=8,65 г/см3; γBi=9,79 г/см3; aˊ=-0,00126 1/ %; bˊ=0,28; 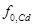 =1,921
=1,921
|
Содержание Cd в сплаве, % масс. |
Молярная доля Cd в сплаве |
Коэффициент активности кадмия, |
||
|
Ур. (1) |
Ур. (3) |
Ур. (5) |
||
|
5,0 |
0,089 |
1,743 |
1,81 |
1,605 |
|
8,5 |
0,147 |
1,647 |
1,742 |
1,701 |
|
14,0 |
0,232 |
1,508 |
1,648 |
1,616 |
|
25,5 |
0,389 |
1,223 |
1,429 |
1,429 |
|
37,0 |
0,522 |
1,067 |
1,371 |
1,385 |
|
48,0 |
0,632 |
0,975 |
1,279 |
1,286 |
|
61,0 |
0,744 |
0,946 |
1,189 |
1,182 |
|
68,0 |
0,798 |
0,934 |
1,148 |
1,141 |
|
80,0 |
0,881 |
0,952 |
1,085 |
1,074 |
|
91,0 |
0,949 |
0,973 |
1,036 |
1,03 |
|
96,0 |
0,978 |
0,987 |
1,015 |
1,013 |
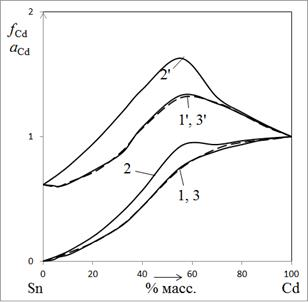
Рис. 2. Активность (1, 2, 3) и коэффициенты активности (1ˊ, 2ˊ, 3ˊ) Cd в матрице сплавов Cd-Sn при его растворении в 1 М NaClO4 в условиях локальной вольтамперометрии. 1, 2, 3 — ур. (1) и (6), (3) и (6), (5) и (6) соответственно. 1ˊ, 2ˊ, 3ˊ — ур. (1), (3) и (5) соответственно.
Таблица 2
Коэффициенты активности кадмия в матрице сплавов кадмий-олово при его растворении в 1 М NaClO4в условиях локальной вольтамперометрии МCd=112,41 г/моль; МSn=118,71 г/моль; γCd=8,65 г/см3; γBi=7,31 г/см3; aˊ=-0,026 1/ %; bˊ=1,543 (при 0÷70 % масс Cd); aˊ=-0,0019 1/ %; bˊ=0,293 (при 70÷100 % масс Cd)
|
Содержание Cd в сплаве, %масс. |
Молярная доля Cd в сплаве |
Коэффициент активности кадмия, |
||
|
Ур. (1) |
Ур. (3) |
Ур. (5) |
||
|
4,0 |
0,042 |
0,262 |
0,668 |
0,500 |
|
6,5 |
0,068 |
0,500 |
0,704 |
0,541 |
|
11,0 |
0,115 |
0,504 |
0,775 |
0,639 |
|
21,5 |
0,224 |
0,742 |
0,970 |
0,727 |
|
32,0 |
0,332 |
0,873 |
1,199 |
0,886 |
|
40,0 |
0,413 |
1,179 |
1,380 |
1,068 |
|
55,5 |
0,568 |
1,332 |
1,629 |
1,313 |
|
70,0 |
0,711 |
1,245 |
1,316 |
1,270 |
|
80,0 |
0,808 |
1,157 |
1,195 |
1,180 |
|
90,0 |
0,906 |
1,083 |
1,090 |
1,076 |
Литература:
1. Рублинецкая Ю. В., Слепушкин В. В., Муковнина Г. С., Гаркушин И. К. // Изв. вузов. Химия и хим. технология. 1999. Т. 42. № 6. С. 149–151.
2. Рублинецкая Ю. В. // Изв. Самарского научного центра РАН. Спец. выпуск «Химия и хим. технология». 2004. С. 40–48
3. Слепушкин В. В., Рублинецкая Ю. В. Муковника Г. С., Коврига Ю. П., Назмутдинов А. Г. // Изв. вузов. Химия и хим. технология. 2001. Т. 44. № 5. С. 80–82.
4. Рублинецкая Ю. В., Слепушкин В. В., Муковнина Г. С., Коврига Ю. П., Назмутдинов А. Г. // Изв. вузов. Химия и хим. технология. 2001. Т. 44. № 5. С. 83.
5. Слепушкин В. В., Рублинецкая Ю. В. Локальный электрохимический анализ. М.: Физматлит. 2010. 312 с.
6. Рублинецкая Ю. В., Слепушкин В. В., Ильиных Е. О., Суськина Е. Л. // Изв. вузов. Северо-Кавказский регион. Естественные науки. Спец. выпуск «Проблемы электрохимии и экологии». 2008. С. 81–83.
Ключевые слова
активность, градуировочные характеристики, локальная вольтамперометрия, коэффициенты активности, анодное растворение гетерогенных сплавов, парциальные токиПохожие статьи
Определение активности компонентов в биметаллическом...
Ключевые слова: активность, коэффициент активности, мольная доля, идеальный раствор, реальный раствор.
Коэффициент активности компонента в растворе показывает [1] на какую величину отклоняются свойства реального раствора от идеального раствора.
Фазовые равновесия в многокомпонентных смесях, содержащих...
Коэффициенты активности растворяющейся фазы гетерогенного...
где NA, NВ — молярная доля компонентов в сплаве; IAmax, IВmax — максимальный ток растворения чистых компонентов.
Коррозионное поведение сплава ЛС59–1 в растворе карбоната...
Содержание цинка имеди впродуктах коррозии сплава ЛС59–1 икоэффициенты селективного растворения компонентов сплава.
Маршаков И. К., Введенский А. В., Кондрашин В. Ю., Боков Г. А. Анодное растворение и селективная коррозия сплавов.
Изменение структуры и состава нитридного слоя при...
Образование ε'-фазы происходит только при азотировании стали и сплавов при наличии углерода в их матрице и имеет карбонитридный характер.
где, – давление насыщенного пара компонента B над раствором; – мольная доля Bкомпонента; – константа Генри.
Установление состава комплекса по методу изомолярных серий...
Определение активности компонентов в биметаллическом расплаве. Первый вывод по методу наименьших квадратов
Используя уравнения (4) и (5) определяем и по Генри: Результаты расчетов активностей, коэффициентов активностей и мольных долей заносим в таблицу 5.
Значение серосодержащих реагентов в амперометрическом...
где М–молярная концентрация раствора при температуре t оС
a–коэффициент теплового расширения данного растворителя; Dt–разность между температурами во время титрования и при стандартизации раствора титранта.
Взаимосвязь между коррозионными и энергетическими...
Однако гетерогенный процесс коррозионного растворения металлических материалов, как известно, начинается с его поверхности
Рис. 2. Анодные поляризационные кривые титана и его сплавов в 40 %-ой серной кислоте при комнатной температуре: 1 — Титан; 2 — Ti08Zr02; 3...
Изучение процесса получения гидантоина как промежуточного...
Гидантоин не является единственным продуктом реакции (его массовая доля составляет 75 %). Наряду с гидантоином в процессе реакции получаются
Коррозионное поведение сплава ЛС59–1 в растворе карбоната...
Флотоэкстракция ионов никеля из водных растворов
Оптимальное мольное отношение Ni:С15Н31СООК:ТВА=1:2:1, при этом степень удаления никеля составила около 95 %.
– эффективность процесса не зависит от объема органической фазы, коэффициента распределения вещества, которое извлекается
Похожие статьи
Определение активности компонентов в биметаллическом...
Ключевые слова: активность, коэффициент активности, мольная доля, идеальный раствор, реальный раствор.
Коэффициент активности компонента в растворе показывает [1] на какую величину отклоняются свойства реального раствора от идеального раствора.
Фазовые равновесия в многокомпонентных смесях, содержащих...
Коэффициенты активности растворяющейся фазы гетерогенного...
где NA, NВ — молярная доля компонентов в сплаве; IAmax, IВmax — максимальный ток растворения чистых компонентов.
Коррозионное поведение сплава ЛС59–1 в растворе карбоната...
Содержание цинка имеди впродуктах коррозии сплава ЛС59–1 икоэффициенты селективного растворения компонентов сплава.
Маршаков И. К., Введенский А. В., Кондрашин В. Ю., Боков Г. А. Анодное растворение и селективная коррозия сплавов.
Изменение структуры и состава нитридного слоя при...
Образование ε'-фазы происходит только при азотировании стали и сплавов при наличии углерода в их матрице и имеет карбонитридный характер.
где, – давление насыщенного пара компонента B над раствором; – мольная доля Bкомпонента; – константа Генри.
Установление состава комплекса по методу изомолярных серий...
Определение активности компонентов в биметаллическом расплаве. Первый вывод по методу наименьших квадратов
Используя уравнения (4) и (5) определяем и по Генри: Результаты расчетов активностей, коэффициентов активностей и мольных долей заносим в таблицу 5.
Значение серосодержащих реагентов в амперометрическом...
где М–молярная концентрация раствора при температуре t оС
a–коэффициент теплового расширения данного растворителя; Dt–разность между температурами во время титрования и при стандартизации раствора титранта.
Взаимосвязь между коррозионными и энергетическими...
Однако гетерогенный процесс коррозионного растворения металлических материалов, как известно, начинается с его поверхности
Рис. 2. Анодные поляризационные кривые титана и его сплавов в 40 %-ой серной кислоте при комнатной температуре: 1 — Титан; 2 — Ti08Zr02; 3...
Изучение процесса получения гидантоина как промежуточного...
Гидантоин не является единственным продуктом реакции (его массовая доля составляет 75 %). Наряду с гидантоином в процессе реакции получаются
Коррозионное поведение сплава ЛС59–1 в растворе карбоната...
Флотоэкстракция ионов никеля из водных растворов
Оптимальное мольное отношение Ni:С15Н31СООК:ТВА=1:2:1, при этом степень удаления никеля составила около 95 %.
– эффективность процесса не зависит от объема органической фазы, коэффициента распределения вещества, которое извлекается