Разработана нелинейная математическая модель колебаний буровой установки под действием периодических нагрузок, представленная системой нелинейных обыкновенных дифференциальных уравнений. Предложена методика расчета основных характеристик колебаний с применением метода многочленных преобразований. Получены расчетные формулы согласно методу многочленных преобразований.
Ключевые слова: математическое моделирование, колебания, динамические нагрузки, дифференциальные уравнения.
Введение. Среди разнообразных видов механического воздействия на различные технические объекты можно выделить периодические. Причины их возникновения разнообразные. Это и внешние воздействия, вызванные, например, порывами ветра, и внутренние, вызванные работой различных устройств, содержащихся в технических объектах. Вибрационные нагрузки возникают при работе различных моторов, насосов, двигателей и постоянно работающих устройств [25]. Элементы объектов, изготовленные из различных материалов, имеют внутренние дефекты, которые могут при вибрационных нагрузках постепенно «развиваться» [4, 14, 21, 39, 50, 60–63]. Рост дефектов особенно при наличии агрессивного химического или биологического воздействия на них может со временем привести не только к разрушению отдельного элемента объекта, но и разрушению объекта в целом [25]. Оценить воздействие вибрационных нагрузок можно экспериментально, проведя серию экспериментов. Но этот путь сложный и дорогой, поскольку требует значительных материальных ресурсов [36, 59]. Второй — теоретический, основанный на анализе математической модели технического объекта [1, 2, 22–24, 52–54, 56, 58], позволяющий оценить границы устойчивой работы механической системы. Точность результатов при таком анализе будет зависеть от того, насколько точна математическая модель объекта. Математическое моделирование позволяет не только спрогнозировать возможное поведение технического объекта при различных динамических режимах его работы, но и оценить влияние конструкционных изменений на его работоспособность. Результаты решения математических задач механики могут быть использованы и используются при моделировании процессов, происходящих в живых системах [3, 5, 19, 47, 55, 65].
Математические методы. Буровая установка представляет собой комплекс машин и механизмов для бурения скважин и шахтных стволов. Буровые установки предназначены для строительства нефтяных и газовых скважин, разведки месторождений полезных ископаемых, подземных вод. В зависимости от вида бурения длины и диаметра ствола в буровые установки входят следующие узлы: буровая вышка, кабина управления, рабочая площадка, платформа основания, буровая лебёдка, подъёмник, вращательный механизм, двигатели внутреннего сгорания, дизель-генераторная станция, электродвигатели, буровой насос, компрессор, резервуар, трубопроводы, система управления буровых установок; контрольно-измерительная система.
Математические модели таких систем представляют собой задачу Коши для системы линейных или нелинейных обыкновенных дифференциальных уравнений [6–9, 12, 34, 48, 49, 57, 58, 64]. Исследование нелинейных систем представляет собой более сложную задачу по сравнению с исследованием линейных систем [18, 26–30]. В теории нелинейных динамических систем применяются различные методы, к числу которых относятся метод усреднения, метод малого параметра, метод Крылова-Боголюбова, метод многочленных преобразований, метод Ван-дер-Поля, метод гармонического баланса, метод возмущений Пуанкаре [6, 10, 11, 64]. Для расчета нелинейной системы с шестью степенями свободы применен метод многочленных преобразований [13, 35]. В методе в результате многочленных преобразований исходная система нелинейных дифференциальных уравнений приводится к автономному виду.
В методе усреднения и Ван-дер-Поля рассматривается укороченное уравнение и находится приближенное решение, не учитывающее все слагаемые нелинейного полинома высокой степени. В методе гармонического баланса приближенное решение учитывает только составляющие основной частоты. В методе малого параметра и возмущений приближенное решение ищется в виде степенного ряда с малым параметром, если ряд сходится, и точность существенно зависит от количества поправок к нулевому приближению. В результате применения метода многочленных преобразований, уравнения движения системы приводиться к автономному виду, определяются параметры системы, характеризующие переходные процессы и установившиеся режимы колебаний.
Математическая модель. Рассмотрим схему буровой установки (рис. 1), состоящую из кабины управления массой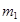 
установленной на рабочую площадку массой 
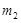, которая в свою очередь установлена на платформу массой 
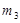для двигателей и ротора, закреплённую на вибрирующей поверхности бурения. В качестве объекты виброзащиты выберем кабину управления.
При длительной эксплуатации сооружения в различных элементах конструкции вибрационные нагрузки могут вызвать рост микротрещин и микропор [31, 32, 37, 38, 41, 43], на рост которых влияет и агрессивность среды [40, 42, 44–46]. Такое влияние можно учесть, приняв зависящей от времени амплитуду внешней нагрузки [60–63]. Процесс разрушения может происходить достаточно долго даже в случай возникновения частых аварийных ситуаций [64]. Поэтому в модели установки он не учитывается. Не учитывается также и возможное возникновение резонансов, вызванных как внутренними, так и внешними возмущениями.
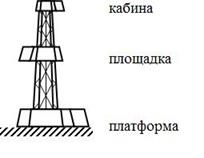
Рис. 1. Схема буровой установки
Обозначим горизонтальные и вертикальные координаты центра масс относительно положению равновесия: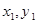 
— кабины управления, 
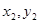— рабочей площадки и 
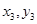— платформы двигателей и ротора.
Предполагается, что упругие элементы связей кабины управления, рабочей площадки и платформы двигателей имеют вид полинома третей степени относительно обобщенной q координаты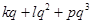 
, демпфирующие элементы связей имеют нелинейную кубическую характеристику 
.
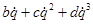На поверхность бурения воздействуют горизонтальные и вертикальные силы в виде периодических функций: 
, 
.
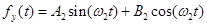Для получения уравнений движения виброзащитной системы используем уравнения Лагранжа в обобщенных координатах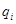 
.
,
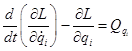где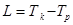 
— функция Лагранжа равная разности кинетической и потенциальной энергии, 
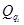— обобщенная сила, соответствующая обобщенной координате .
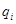Общая кинетическая энергия системы определяется как сумма кинетических энергий отдельных элементов установки:
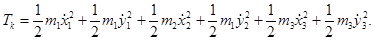
Аналогичным образом определяется и потенциальная энергия системы
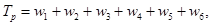
где
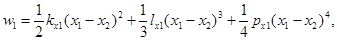
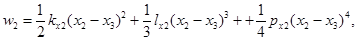
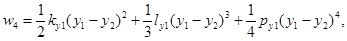
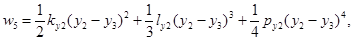
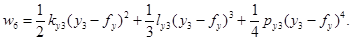
Обобщенные силы равны:
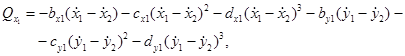
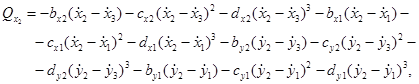
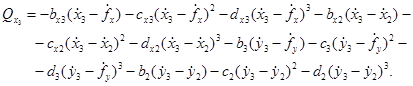
Подставим выражения для 
в уравнения Лагранжа, получим систему шести нелинейных дифференциальных уравнений второго порядка:
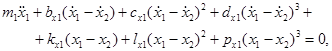
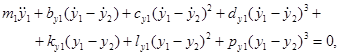
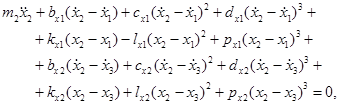
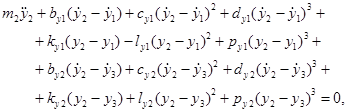
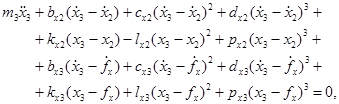
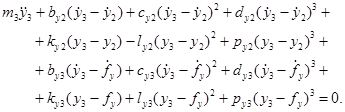
Здесь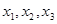
— абсолютные горизонтальные координаты центра масс и 
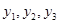— абсолютные вертикальные координаты центра масс относительно положению равновесия системы
Введем относительные координаты по отношению к колебаниям поверхности бурения.
.
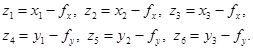Запишем систему нелинейных уравнений движения в новых переменных:
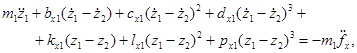
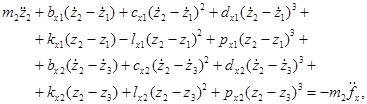
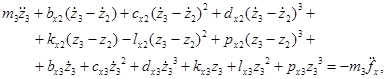
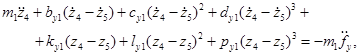
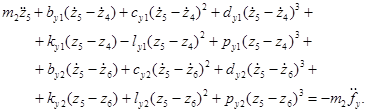
Для записи периодических функций введем комплексные переменные
, 
.
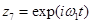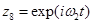В новых переменных периодические функции правых частей системы можно записать в виде:
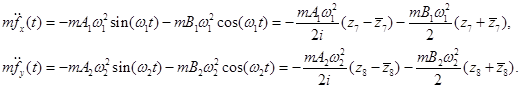
Решение уравнений. В отличие от методов расчета, предложенных в [7] ниже используется метод многочленных преобразований [13].
Запишем систему уравнений в матричной форме:
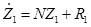, где 
-нелинейный вектор системы,
.
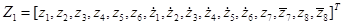В результате линейной замены переменных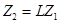 
, получим систему дифференциальных уравнений с линейной диагональной матрицей вида 
.
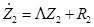В соответствии с методом, изложенным в [13], выполним многочленную замену переменных:
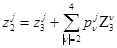, (j=1…12).
В результате многочленного преобразования, с точностью до членов четвертого порядка, получаем автономную систему дифференциальных уравнений:
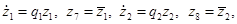
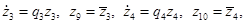
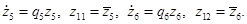
Решение автономной системы уравнений можно представить в виде:
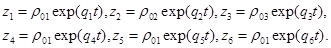
Численный эксперимент. Рассчитан переходный и установившийся режимы колебаний буровой установки при следующих параметрах:
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
.
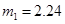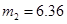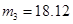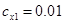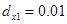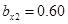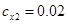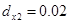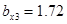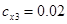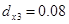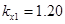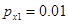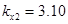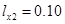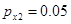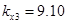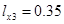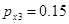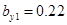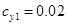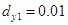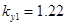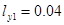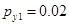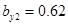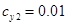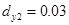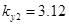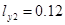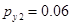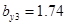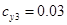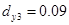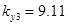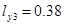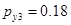На поверхность бурения воздействуют горизонтальные и вертикальные силы:
, 
.
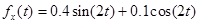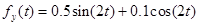Согласно методу многочленных преобразований [13] определены коэффициенты преобразованной автономной системы
.
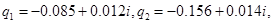
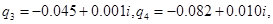
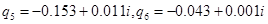Методом многочленных преобразований получен установившийся полигармонический режим колебаний системы:
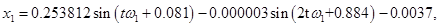
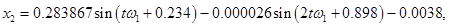
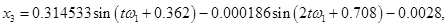
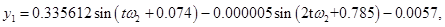
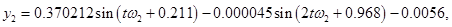
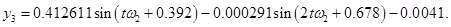
Некоторые из результатов численных результатов представлены на рис. 2–6. На рис. 2 и 3 представлены графики изменения амплитуд колебаний во времени. Колебания системы происходят с частотой внешней силы. На рис. 4 показано абсолютное горизонтальное и вертикальное перемещение при установлении колебаний. Вынужденные колебания в начале установления являются квазипериодическими. На рис 5. представлены абсолютные колебания в плоскости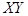 
.
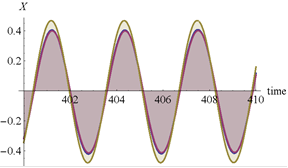
Рис. 2. Зависимость относительных горизонтального и вертикального перемещений установившихся колебаний от времени, 
.
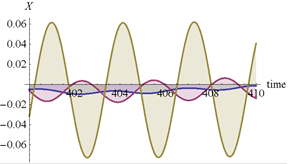
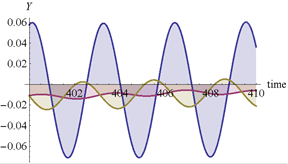
Рис. 3. Зависимость абсолютных горизонтального и вертикального перемещений установившихся колебаний от времени .
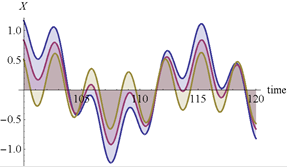
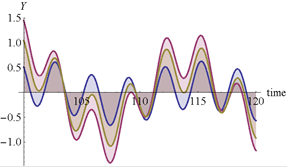
Рис. 4. Зависимость абсолютных горизонтального и вертикального перемещений от времении при установлении колебаний,.
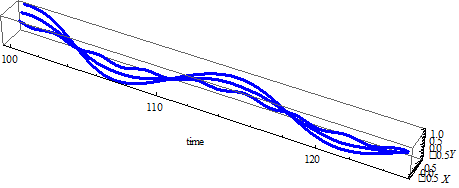
Рис. 5. Формы колебаний в плоскости XY
Сопоставление полученных результатов производилось с численными результатами, полученными при решении задачи Коши для системы дифференциальных уравнений с применением численного метода of the Dormand-Prince type [51–53], учитывающего структурные особенности уравнений, успешно применяемого и для решения дифференциальных уравнений в частных производных [15–17]. Отличие в максимальных отклонения составляло не более 2 %. Численная реализация решения систем дифференциальных уравнений осуществлялась в среде программирования математического пакета MatLab [20, 33].
Заключение. Нелинейная математическая модель буровой установки в виде системы нелинейных дифференциальных уравнений позволяет построить амплитудно-частотную характеристику установки. Применение метода многочленных преобразований дает возможность свести нахождение установившегося режима колебаний менее трудоемкими математическими методами, чем методы решения нелинейных дифференциальных уравнений.
Литература:
1. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
2. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 101–106.
3. Горбунова М. В., Колпак Е. П., Крицкая А. В. Математическая модель антропогенного воздействия на одиночную популяцию / В сборнике: Синергетика в общественных и естественных науках: девятые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. редкол.: Лапина Г. П. (отв. ред.) и др. Тверь, 2013. — С. 165.
4. Даль Ю. М., Пронина Ю. Г Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
5. Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
6. Иванов С. Е. Алгоритмическая реализация метода исследования нелинейных динамических систем // Научно-технический вестник информационных технологий, механики и оптики. — 2012. — № 4 (80). — С. 90–92.
7. Иванов С. Е. Исследование нелинейных динамических систем с тремя степенями свободы // Научно-технический вестник информационных технологий, механики и оптики. — 2011. — № 4 (74). — С. 62–64.
8. Иванов С. Е. Исследование нелинейных колебаний механической системы с тремя степенями свободы на вибрирующей платформе // Научно-технический вестник информационных технологий, механики и оптики. — 2003. — № 9. — С. 29–32.
9. Иванов С. Е. Определение установившихся режимов работы виброзащитной системыа с двумя степенями свободы // Научно-технический вестник информационных технологий, механики и оптики. — 2010. — № 4 (68). — С. 44–46.
10. Иванов С. Е., Мельников В. Г. Применение матричной формы уравнений Лагранжа в компьютерном моделировании // Научно-технический вестник информационных технологий, механики и оптики. — 2006. — № 31. — С. 22–24.
11. Иванов С. Е., Мельников Г. И. Автономизация нелинейных динамических систем // Научно-технический вестник информационных технологий, механики и оптики. — 2014. — № 1 (89). — С. 151–156.
12. Иванов С. Е., Мельников Г. И. Исследование динамики нелинейной приборной системы в условиях кинематических периодических возмущений // Научно-технический вестник информационных технологий, механики и оптики. — 2005. — № 19. — С. 3–7.
13. Иванов С. Е., Мельников Г. И. Разработка алгоритмов метода многочленных преобразований теории нелинейных систем в среде Matlab // Научно-технический вестник информационных технологий, механики и оптики. — 2006. — № 31. — С. 14–17.
14. Кабриц С. А. Некоторые прикладные задачи статики тонких оболочек из эластомеров // диссертация на соискание ученой степени кандидата физико-математических наук / Ленинград, 1984.
15. Кабриц С. А., Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
16. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. — 2001. — № 1. — С. 38.
17. Кабриц С. А., Черных К. Ф. Нелинейная теория изотропно упругих тонких оболочек с учетом поперечного сдвига // Известия Российской академии наук. Механика твердого тела. — 1996. — № 1. — С. 124–136.
18. Кабриц С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2014. — № 2. — С. 261–270.
19. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
20. Колпак Е. П. Mathlab: методы вычислений: учебное пособие / Е. П. Колпак; Санкт-Петербургский гос. ун-т. Санкт-Петербург, 2007.
21. Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
22. Колпак Е. П., Мальцева Л. С. Большие деформации резиновых мембран // Молодой ученый. — 2014. — № 16 (75). — С. 78–84.
23. Колпак Е. П., Мальцева Л. С. Круглая плоская мембрана при больших деформациях // Приволжский научный вестник. — 2014. — № 11–1 (39). — С. 5–10.
24. Колпак Е. П., Мальцева Л. С. Об устойчивости сжатых пластин // Молодой ученый. — 2015. — № 14 (94). — С. 1–8.
25. Круглов Ю. А., Туманов Ю. А. Ударовиброзащита машин и аппаратуры. Л.: Машиностроение, 1986. — 222 с.
26. Мальков В. М., Кабриц С. А., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
27. Мальков В. М., Малькова Ю. В. Анализ сингулярности напряжений в нелинейной задаче Фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. — С. 652–660.
28. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
29. Мальков В. М., Малькова Ю. В. Плоские задачи о сосредоточенных силах для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 83–96.
30. Мальков В. М., Малькова Ю. В. Плоские задачи упругости для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 3. — С. 93–106.
31. Мальков В. М., Малькова Ю. В. Трещина в форме дуги окружности, расположенная вблизи поверхности раздела материалов // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2010. — № 1. — С. 93–104.
32. Мальков В. М., Малькова Ю. В., Степанова В. А. Двухкомпонентная плоскость из материала Джона с межфазной трещиной, нагруженной давлением // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2013. — № 3. — С. 113–125.
33. Мельников В. Г., Иванов С. Е. Применение компьютерных пакетов и анимаций в преподавании механики // Научно-технический вестник информационных технологий, механики и оптики. — 2005. — № 19. — С. 8–11.
34. Мельников Г. И., Иванов С. Е. Исследование нелинейных колебаний голономных систем с тремя степенями свободы на вибрирующем основании // Научно-технический вестник информационных технологий, механики и оптики. — 2004. — № 15. — С. 11–15.
35. Мельников Г. И., Иванов С. Е., Мельников В. Г., Малых К. С. Применение модифицированного метода преобразований к нелинейной динамической системе // Научно-технический вестник информационных технологий, механики и оптики. — 2015. — Т. 15. — № 1 (95). — С. 149–154.
36. Миндлин Ю. Б., Колпак Е. П., Гасратова Н. А. Отличительные признаки кластеров и практика их применения в России // Политика и общество. — 2015. — № 5. — С. 666–675.
37. Пронина Ю. Г. Исследование возможности образования и развития пор в твердых телах в рамках деформационной теории Девиса-Надаи // Известия Российской академии наук. Механика твердого тела. — 2014. — № 3. — С. 79–92.
38. Пронина Ю. Г. Краевая дислокация и сосредоточенная сила в упругой полуплоскости с отверстиями и краевыми вырезами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 4. — С. 120–124.
39. Пронина Ю. Г. Лекции по теории упругости. Общие положения учебное пособие / Пронина Ю. Г.; С.-Петерб. гос. ун-т. СПб., 2004.
40. Пронина Ю. Г. Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121–130.
41. Пронина Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
42. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
43. Пронина Ю. Г. Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2009. — № 1. — С. 113–122.
44. Пронина Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129–135.
45. Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
46. Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
47. Balykina Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433.
48. Besharati S. R., Dabbagh V., Amini H., Akbari J., Hamdi M. Nonlinear Dynamic Analysis of a New Antibacklash Gear Mechanism Design for Reducing Dynamic Transmission Error // Journal of Mechanical Design, Transactions of the ASME. — 2015. — Т. 137. — № 5. — 054502.
49. Chernyshev A. B., Martirosyan K. V., Martirosyan A. V. Analisis of the nonlinear distributed control system's sustainability // Journal of Mathematics and Statistics. — 2014. — Т. 10. — № 3. — С. 316–321.
50. Dal’ Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
51. Ivanov S. E., Melnikov G. I., Melnikov V. G., The modified Poincare-Dulac method in analysis of autooscillations of nonlinear mechanical systems // Journal of Physics: Conference Series. — 2014. — Т. 570, № 022002. — С. 121–126.
52. Kolpak E. P, Ivanov S. E. Mathematical modeling of the system of drilling rig // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 16. — С. 699–708.
53. Kolpak E. P., Ivanov S. E. Mathematical and computer modeling vibration protection system with damper // Applied Mathematical Sciences. — 2015. — Т. 9. — №. 78. — C. 3875–3885.
54. Kolpak E. P., Maltseva L. S., Ivanov S. E. On the stability of compressed plate // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 20. — 933–942.
55. Kolpak E. P., Kabrits S. A., Bubalo V. The follicle function and thyroid gland cancer // Biology and Medicine. — 2015. — Т. 7. — № 1. — С. BM060.15.
56. Laha D., Ren Y., Suganthan P. N. Modeling of steelmaking process with effective machine learning techniques // Expert Systems with Applications. — 2015. — Т. 42. — № 10. — С. 4687–4696.
57. Liu J.-M., Zhou G.-Q. Study on bearing capacity of in-service drilling derricks based on static and dynamic performance // Gongcheng Lixue/Engineering Mechanics. — 2014. — Т. 31. — № 8. — С. 250–256.
58. Mehennaoui Sami, Khochemane Lakhdar Optimization of setting parameters of a rotary drilling rig using simhydraulics toolbox // Contemporary Engineering Sciences. — Т. 8. — № 3. — С. 115–120.
59. Mozzherina E. An Approach to Improving the Classification of the New York Times Annotated Corpus // Communi-cations in Computer and Information Science. — 2013. — Т. 394. — С. 83–91.
60. Pronina Y. G. Lifetime assessment for an ideal elastoplastic thick-walled spherical member under general mechanochemical corrosion conditions // Computational Plasticity XII: Fundamentals and Applications — Proceedings of the 12th International Conference on Computational Plasticity — Fundamentals and Applications, COMPLAS 2013. С. 729–738.
61. Pronina Y. G. Study of possible void nucleation and growth in solids in the framework of the Davis-Nadai deformation theory // Mechanics of Solids. — 2014. — Т. 49. — № 3. — С. 302–313.
62. Pronina Y. G., Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // Int. Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
63. Sedova O. S., Khaknazarova L. A., Pronina Y. G. Stress concentration near the corrosion pit on the outer surface of a thick spherical member // Tenth International Vacuum Electron Sources Conference (IVESC) & Second International Conference on Emission Electronics (ICEE) 2014. С. 245–246.
64. Zhu Y., Jiang W., Zheng Z. Nonlinear dynamic behaviors of electro-hydraulic servo system under friction // Journal of Beijing University of Aeronautics and Astronautics. — 2015. — Т. 41. — № 1. — С. 50–57.
65. Zhukova I. V., Kolpak E. P., Balykina Y. E. Mathematical model of growing tumor // Applied Mathematical Sciences. — 2014. — Т. 8. — № 29–32. — С. 1455–1466.
