В наши дни активно развивается рынок электронной коммерции: все большую популярность набирают интернет-магазины и различные интернет-сервисы. Основным рычагом увеличения продаж интернет-магазина является так называемая конверсия. Конверсия — это отношение числа визитов пользователей, в которых были совершены целевые действия, к общему числу визитов. Целевые действия определяются исходя из коммерческой составляющей страницы. Примеры целевых действий: положить товар в корзину, нажать кнопку «оформить товар», перейти в раздел «контакты» и т. д. Величина конверсии в основном зависит от внешнего оформления интернет-страницы, расположения определенных элементов и функционала.
Основным инструментом увеличения конверсии является тестирование интернет-страниц [1]. Перед тестированием страницы задается определенная цель (например, клик по некоторой кнопке), показатели достижения которой отслеживаются. Пользователям поочередно показываются разные версии одной страницы (например, в одной версии может быть изменена цветовая гамма, расположение элементов и т.д). После проведения теста сравниваются показатели достижения целей, и выявляется страница с большей конверсией.
Подход к тестированию, описанный выше, довольно популярен, однако имеет существенный недостаток: во время теста в равных пропорциях показываются страницы с низкой и высокой конверсией. Показ страниц с низкой конверсией несет убыток организатору теста. Владелец интернет-ресурса, кроме выявления страницы с наибольшей конверсией, заинтересован в том, чтобы во время проведения теста достичь наибольшую суммарную конверсию. Именно эту задачу решает подход к тестированию, основанный на решении задачи о многоруком бандите (Multi-armed bandit [2]).
Цели работы: предложить подход к тестированию интернет-страниц на основе задачи о многоруком бандите, рассмотреть некоторые алгоритмы решения задачи, разработать программную реализацию симуляции тестирования страниц, на основе которой продемонстрировать применимость алгоритмов для решения задачи тестирования.
Задача о многоруком бандите является частным случаем дилеммы исследования-использования, которая может быть описана следующим образом [3]. Имеется система взаимодействия игрока с окружающей средой. Игрок имеет набор действий для этого взаимодействия. После каждого действия игрок получает некоторый выигрыш. Перед очередным взаимодействием с окружающей средой игрок имеет выбор: выполнить уже известное действие и получить выигрыш близкий к ожидаемому или выполнить действие, результат которого трудно предугадать. В первом случае будем говорить, что игрок находится в фазе использования, во втором случае — в фазе исследования.
Задача о многоруком бандите впервые рассмотрена Гербертом Роббинсом (Herbert Ellis Robbins) в 1952 году и с тех пор широко используется для моделирования задач вида исследования-использования. Математическая модель задачи строится следующим образом [4].
Рассмотрим 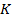 игровых автоматов. С каждым автоматом связаны случайные величины
игровых автоматов. С каждым автоматом связаны случайные величины 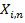 , где
, где 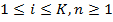 , то есть
, то есть 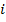 — индекс автомата. При каждой игре на автомате случайная величина генерирует выигрыш. Например, играя на автомате
— индекс автомата. При каждой игре на автомате случайная величина генерирует выигрыш. Например, играя на автомате 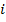 , игрок будет получать выигрыши
, игрок будет получать выигрыши 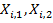 ,... — реализации независимых случайных величин, имеющих общий неизвестный закон распределения с неизвестным математическим ожиданием
,... — реализации независимых случайных величин, имеющих общий неизвестный закон распределения с неизвестным математическим ожиданием 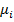 . Независимость распределений имеет место и для выигрышей разных автоматов, то есть
. Независимость распределений имеет место и для выигрышей разных автоматов, то есть 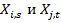 независимы (и, как правило, имеют разные законы распределения) для любых
независимы (и, как правило, имеют разные законы распределения) для любых 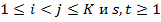 . Цель игрока — достичь максимальный выигрыш за время игры.
. Цель игрока — достичь максимальный выигрыш за время игры.
Под стратегией (policy, allocation strategy) 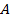 будем понимать алгоритм выбора следующего автомата для игры на основе последовательности предыдущих игр и полученных выигрышей. Основной характеристикой сравнения стратегий является функция потерь.
будем понимать алгоритм выбора следующего автомата для игры на основе последовательности предыдущих игр и полученных выигрышей. Основной характеристикой сравнения стратегий является функция потерь.
Пусть 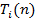 — это число игр, сыгранных на автомате
— это число игр, сыгранных на автомате 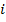 c использованием стратегии
c использованием стратегии 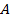 в течение первых
в течение первых 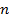 игр. Тогда функция потерь стратегии
игр. Тогда функция потерь стратегии 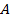 после
после 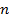 сыгранных игр определяется как
сыгранных игр определяется как
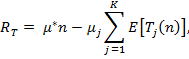
где 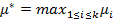 .
.
Если бы распределения выигрышей были известны, то стратегия игры была бы тривиальна: всегда играть на автомате, который имеет максимальное математическое ожидание выигрыша.
Доказано [2], что для функции потерь справедлива оценка 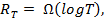 где
где 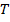 — количество сыгранных игр. Алгоритмы, которые достигают этой оценки, называются оптимальными. В дальнейшем будут использоваться следующие обозначения:
— количество сыгранных игр. Алгоритмы, которые достигают этой оценки, называются оптимальными. В дальнейшем будут использоваться следующие обозначения: 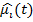 — средний выигрыш автомата
— средний выигрыш автомата 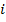 после
после 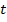 игр,
игр, 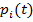 — вероятность игры на автомате
— вероятность игры на автомате 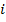 во время
во время 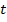 . Ниже приведены идеи и краткие описания используемых алгоритмов.
. Ниже приведены идеи и краткие описания используемых алгоритмов.
Обзор литературы
Описание задачи и алгоритмов её решения, к сожалению, крайне скудно представлено в русскоязычной литературе, в связи с чем, при исследовании и написании работы использовались в основном англоязычные источники. Постановка задачи и описание некоторых подходов к решению описаны в [3]. В [2] вводится функция, называемая сожалением, которая характеризует работу алгоритмов для решения задачи о многоруком бандите. Там же доказано, что функция сожаления 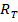 асимптотически не меньше функции
асимптотически не меньше функции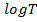 . Описание используемых в работе алгоритмов и демонстрация их работы представлены в [4]. В [5] описан алгоритм UCB1 и даны оценки функции сожаления
. Описание используемых в работе алгоритмов и демонстрация их работы представлены в [4]. В [5] описан алгоритм UCB1 и даны оценки функции сожаления 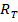 некоторых алгоритмов.
некоторых алгоритмов.
Описание алгоритмов
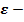 жадный алгоритм (
жадный алгоритм (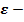 greedy)
greedy)
Алгоритм 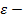 greedy [4, 1] относится к так называемым жадным алгоритмам, которые отличаются тем, что на каждом этапе оптимизационной задачи выбирают локально оптимальное решение, допуская, что конечное решение также окажется оптимальным.
greedy [4, 1] относится к так называемым жадным алгоритмам, которые отличаются тем, что на каждом этапе оптимизационной задачи выбирают локально оптимальное решение, допуская, что конечное решение также окажется оптимальным.
В силу простоты реализации 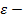 жадный алгоритм широко используется для решения задачи о многоруком бандите. Суть алгоритма состоит в том, что в каждый момент времени
жадный алгоритм широко используется для решения задачи о многоруком бандите. Суть алгоритма состоит в том, что в каждый момент времени 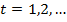 выбирается автомат с наибольшим средним выигрышем с вероятностью
выбирается автомат с наибольшим средним выигрышем с вероятностью 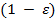 и с вероятностью
и с вероятностью 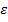 — случайный автомат среди всех. Формально, пусть после
— случайный автомат среди всех. Формально, пусть после 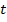 игр средние выигрыши автоматов равны
игр средние выигрыши автоматов равны 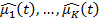 тогда вероятность выбора автомата с номером
тогда вероятность выбора автомата с номером 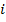 в следующий момент времени вычисляется по формуле
в следующий момент времени вычисляется по формуле
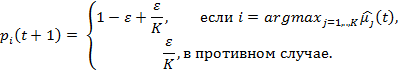
На каждом шаге с вероятностью 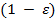 алгоритм находится в фазе использования и с вероятностью
алгоритм находится в фазе использования и с вероятностью 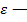 в фазе исследования. При
в фазе исследования. При 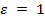 получим стратегию, при которой номер автомата для следующей игры выбирается случайно, а при ε = 0 получим так называемый «чистый» жадный алгоритм, который никогда не будет иметь фазу исследования.
получим стратегию, при которой номер автомата для следующей игры выбирается случайно, а при ε = 0 получим так называемый «чистый» жадный алгоритм, который никогда не будет иметь фазу исследования.
В [5] предложена модификация данного алгоритма, в которой значение параметра ε уменьшается с течением времени.
Модифицированный ε — жадный алгоритм (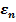 — greedy)
— greedy)
Алгоритм 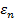 – greedy [5, 6] отличается от предыдущего алгоритма тем, что на каждом шаге
– greedy [5, 6] отличается от предыдущего алгоритма тем, что на каждом шаге 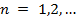 вероятность
вероятность 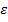 вычисляется по формуле
вычисляется по формуле
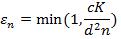
где 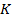 — число автоматов,
— число автоматов, 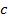 и
и 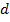 — параметры, причем
— параметры, причем 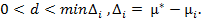 В [5] доказано, что данный алгоритм является оптимальным. Два приведенных выше алгоритма обладают существенными недостатками. Первый из которых заключается в том, что в фазе исследования номер автомата для следующей игры выбирается случайно, то есть независимо от полученных выигрышей. Второй недостаток состоит в том, что вероятность попадания в фазу исследования не зависит от полученных выигрышей, тогда как представляется правильным увеличивать данную вероятность в случае наличия автоматов с близкими выигрышами. От обоих недостатков свободен следующий алгоритм.
В [5] доказано, что данный алгоритм является оптимальным. Два приведенных выше алгоритма обладают существенными недостатками. Первый из которых заключается в том, что в фазе исследования номер автомата для следующей игры выбирается случайно, то есть независимо от полученных выигрышей. Второй недостаток состоит в том, что вероятность попадания в фазу исследования не зависит от полученных выигрышей, тогда как представляется правильным увеличивать данную вероятность в случае наличия автоматов с близкими выигрышами. От обоих недостатков свободен следующий алгоритм.
Алгоритм Softmax
Алгоритм описан в [4]. Его идея состоит в том, чтобы играть на автомате с вероятностью пропорциональной среднему выигрышу. Пусть после 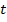 игр средние выигрыши автоматов равны
игр средние выигрыши автоматов равны 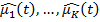 , тогда вероятность того, что в момент времени
, тогда вероятность того, что в момент времени 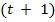 будет сыгран автомат с номером
будет сыгран автомат с номером 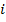 равна
равна
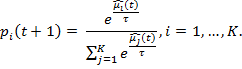
Параметр 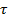 называется температурным коэффициентом. При
называется температурным коэффициентом. При 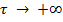 алгоритм ведет себя случайным образом, при
алгоритм ведет себя случайным образом, при 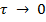 алгоритм становится жадным.
алгоритм становится жадным.
Алгоритм UCB1
UCB (Upper Confidence Bounds) — семейство алгоритмов, которое описано в [5] как простая реализация идеи оптимизма в условиях неопределенности, предложенной в [2]. Рассмотрим самый простой в реализации и популярный алгоритм UCB1.
На каждом шаге алгоритма вычисляется величина
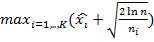 ,
,
где 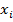 — средний выигрыш автомата
— средний выигрыш автомата 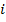 ,
, 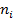 — количество сыгранных игр на автомате
— количество сыгранных игр на автомате 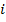 ,
, 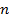 — количество всех сыгранных игр. Алгоритм выбирает тот автомат, для которого эта величина максимальна. Таким образом, видно, что алгоритм, выбирая автомат для следующей игры, использует информацию о количестве сыгранных игр на каждом автомате. Рассмотренный алгоритм отличается от ранее описанных главным образом тем, что не имеет параметров, следовательно, нет необходимости в их подборе. Другим отличием алгоритма является его полная детерминированность, то есть отсутствие случайности.
— количество всех сыгранных игр. Алгоритм выбирает тот автомат, для которого эта величина максимальна. Таким образом, видно, что алгоритм, выбирая автомат для следующей игры, использует информацию о количестве сыгранных игр на каждом автомате. Рассмотренный алгоритм отличается от ранее описанных главным образом тем, что не имеет параметров, следовательно, нет необходимости в их подборе. Другим отличием алгоритма является его полная детерминированность, то есть отсутствие случайности.
Алгоритм погони (Pursuit)
Алгоритм описан в [4]. На каждом шаге вычисляются вероятности выбора каждого автомата для следующей игры по формуле
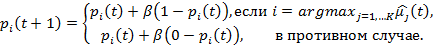
На первом шаге считаем, что 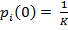 . Параметр
. Параметр 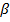 называется скоростью обучения.
называется скоростью обучения.
Проведение эксперимента
Модель Бернулли многорукого бандита
Модель Бернулли многорукого бандита [5] отличается тем, что случайные величины, характеризующие выигрыш в игре на автоматах, имеют распределение Бернулли с неизвестными вероятностями 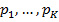 . Таким образом, при игре на автомате с номером
. Таким образом, при игре на автомате с номером 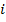 игрок получает выигрыш
игрок получает выигрыш 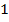 с вероятностью
с вероятностью 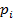 и выигрыш 0 с вероятностью
и выигрыш 0 с вероятностью 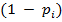 . Данный частный случай задачи о многоруком бандите подходит для моделирования процесса тестирования интернет-страниц. Будем считать, что показ страницы — это игра на автомате, а выигрыш
. Данный частный случай задачи о многоруком бандите подходит для моделирования процесса тестирования интернет-страниц. Будем считать, что показ страницы — это игра на автомате, а выигрыш 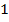 — есть достижение конверсионной цели.
— есть достижение конверсионной цели.
Описание эксперимента
В качестве эксперимента, иллюстрирующего работу описанных выше алгоритмов, предложена программная реализация симуляции тестирования интернет-страниц. На вход программе подается число тестируемых страниц 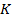 , вектор вероятностей
, вектор вероятностей 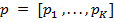 , где компонента
, где компонента 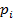 — есть вероятность достижения конверсионной цели на странице с номером
— есть вероятность достижения конверсионной цели на странице с номером 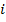 . Кроме того, задается число показов страниц
. Кроме того, задается число показов страниц 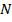 . Программная реализация выполнена на языке Python. В качестве результатов работы программы выводится величина конверсии, достигнутой каждым алгоритмом, и номер страницы с наибольшей конверсией. Под конверсией в данной случае понимается отношение числа достигнутых целей к общему числу показов страниц
. Программная реализация выполнена на языке Python. В качестве результатов работы программы выводится величина конверсии, достигнутой каждым алгоритмом, и номер страницы с наибольшей конверсией. Под конверсией в данной случае понимается отношение числа достигнутых целей к общему числу показов страниц 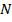 .
.
Поскольку 4 из 5 рассмотренных алгоритмов зависят от параметров, которые влияют на их работу (см. пример на рис  ), то не представляется возможным подобрать параметры алгоритмов, которые гарантировали бы достижение наибольшей конверсии на всех векторах
), то не представляется возможным подобрать параметры алгоритмов, которые гарантировали бы достижение наибольшей конверсии на всех векторах 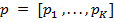 . С этим же связана проблема невозможности выявления алгоритма, который бы работал на всех векторах
. С этим же связана проблема невозможности выявления алгоритма, который бы работал на всех векторах 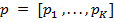 наилучшим образом.
наилучшим образом.
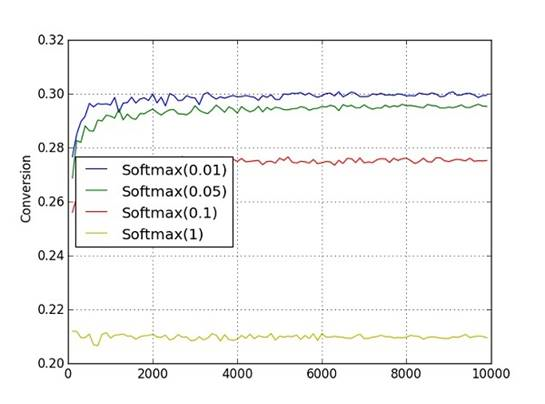
Рис. 1: Зависимость работы алгоритма Softmax от параметров
Результаты и выводы
Рассмотрим несколько случаев входных данных, на которых продемонстрируем работу алгоритмов и сравним полученные результаты. Сначала рассмотрим случай тестирования двух страниц 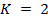 . Пусть
. Пусть 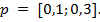 Параметры алгоритмов были подобраны в ходе экспериментов. Результаты работы алгоритмов представлены в таблице
Параметры алгоритмов были подобраны в ходе экспериментов. Результаты работы алгоритмов представлены в таблице 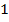 и на рисунке
и на рисунке  .
.
Все алгоритмы, за исключением UCB1, имеют элемент случайности, поэтому для них в качестве результатов берется среднее значение для 100 запусков.
Из таблицы  и графика
и графика  видно, что результаты работы алгоритмов приблизительно совпадают. Следует отметить, что алгоритм Softmax в большинстве случаев достигал наибольшей конверсии среди всех алгоритмов. Кроме того, видно, что алгоритм UCB1 имеет медленный рост достигаемой конверсии, однако при большом числе показов страниц
видно, что результаты работы алгоритмов приблизительно совпадают. Следует отметить, что алгоритм Softmax в большинстве случаев достигал наибольшей конверсии среди всех алгоритмов. Кроме того, видно, что алгоритм UCB1 имеет медленный рост достигаемой конверсии, однако при большом числе показов страниц 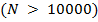 не уступает другим алгоритмам.
не уступает другим алгоритмам.
Таблица 1
Достигнутая конверсия: случай тестирования двух страниц
|
Алгоритм\Показы |
1000 |
5000 |
10000 |
20000 |
50000 |
|
|
0,2946 |
0,2991 |
0,2983 |
0,2988 |
0,299 |
|
|
0,2934 |
0,2983 |
0,2993 |
0,2937 |
0,2996 |
|
Softmax(0,01) |
0,3 |
0,2981 |
0,2991 |
0,3004 |
0,2999 |
|
Pursuit(0.05) |
0,295 |
0,2941 |
0,2975 |
0,2999 |
0,3001 |
|
UCB1 |
0,2714 |
0,2893 |
0,2937 |
0,2962 |
0,2999 |
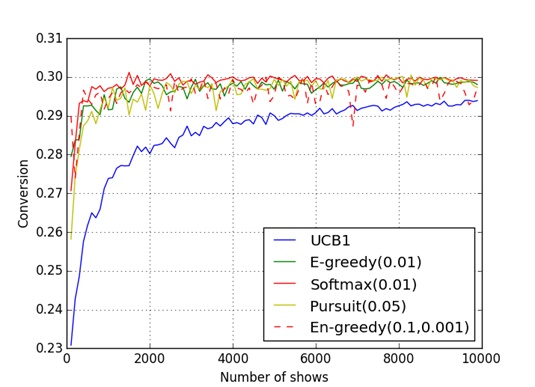
Рис. 2: Результат работы программы для двух тестируемых страниц
В таблице 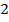 и на рисунке
и на рисунке 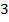 приведены результаты работы алгоритмов для тестирования
приведены результаты работы алгоритмов для тестирования 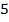 страниц. Вектор вероятностей имеет вид
страниц. Вектор вероятностей имеет вид 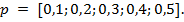
Таблица 2
Достигнутая конверсия: случай тестирования пяти страниц
|
Алгоритм\Показы |
1000 |
5000 |
10000 |
20000 |
50000 |
|
|
0,4645 |
0,483 |
0,4806 |
0,49 |
0,4925 |
|
|
0,4473 |
0,485 |
0,4861 |
0,4944 |
0,4975 |
|
Softmax(0,01) |
0,4718 |
0,4794 |
0,472 |
0,4847 |
0,4882 |
|
Pursuit(0.01) |
0,4516 |
0,4844 |
0,486 |
0,4957 |
0,4938 |
|
UCB1 |
0,4214 |
0,4633 |
0,476 |
0,4865 |
0,4927 |
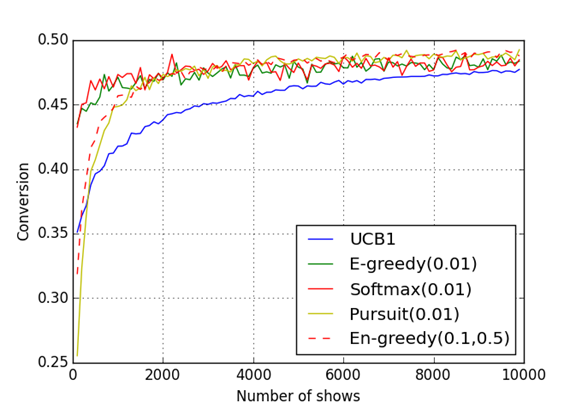
Рис. 3: Результат работы программы для 5 тестируемых страниц
Из таблицы 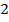 видно, что для
видно, что для 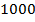 показов наибольшую конверсию достиг алгоритм Softmax, при
показов наибольшую конверсию достиг алгоритм Softmax, при 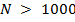 наилучшим образом сработали Pursuit и
наилучшим образом сработали Pursuit и 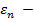 greedy.
greedy.
Теперь рассмотрим случай 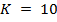 с вектором вероятностей
с вектором вероятностей
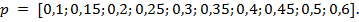
Результаты работы алгоритмов приведены в таблице  и на рисунке
и на рисунке  . В данном случае наибольшую конверсию достигали алгоритмы
. В данном случае наибольшую конверсию достигали алгоритмы 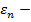 greedy и Pursuit.
greedy и Pursuit.
Таблица 3
Достигнутая конверсия: случай тестирования десяти страниц
|
Алгоритм\Показы |
1000 |
5000 |
10000 |
20000 |
50000 |
|
|
0,5483 |
0,5714 |
0,5746 |
0,5802 |
0,5847 |
|
|
0,5307 |
0,5753 |
0,583 |
0,5938 |
0,5903 |
|
Softmax(0,01) |
0,5441 |
0,5563 |
0,579 |
0,5781 |
0,5719 |
|
Pursuit(0.01) |
0,5382 |
0,5817 |
0,5807 |
0,5838 |
0,5874 |
|
UCB1 |
0,4464 |
0,5268 |
0,554 |
0,5729 |
0,5864 |
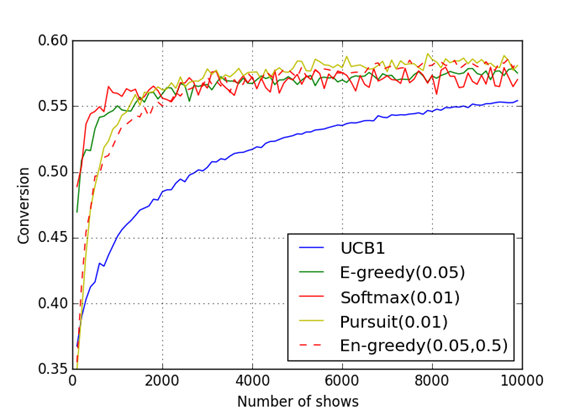
Рис. 4: Результат работы программы для 10 тестируемых страниц
Рассмотрим случай, когда конверсии страниц имеют близкие значения, что наиболее часто встречается на практике. Пусть 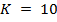 и вектор конверсионных вероятностей имеет вид
и вектор конверсионных вероятностей имеет вид
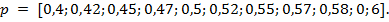
Результат работы алгоритмов представлен в таблице 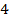 и на рисунке
и на рисунке 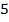 .
.
Таблица 4
Сравнение работы алгоритмов тестирования 10 страниц
|
Алгоритм\Показы |
1000 |
5000 |
10000 |
20000 |
50000 |
|
|
0,5658 |
0,5766 |
0,5818 |
0,5844 |
0,5886 |
|
|
0,5599 |
0,5784 |
0,5814 |
0,5814 |
0,59 |
|
Softmax(0,01) |
0,5659 |
0,5796 |
0,5814 |
0,5828 |
0,5857 |
|
Pursuit(0.01) |
0,5578 |
0,5827 |
0,5842 |
0,5839 |
0,5893 |
|
UCB1 |
0,5293 |
0,5451 |
0,5544 |
0,5635 |
0,576 |
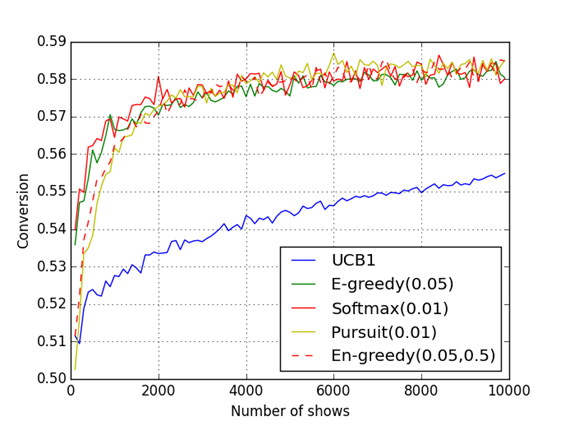
Рис. 5: Результат работы программы для 10 тестируемых страниц (случай страниц с близкой конверсией)
В рассматриваемом случае важно то, с каким успехом алгоритмы находят страницу с наибольшей конверсией. В таблице 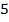 представлены результаты работы алгоритмов при
представлены результаты работы алгоритмов при 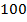 запусках. В ячейках — число запусков, в которых алгоритм обнаружил страницу с наибольшей конверсией.
запусках. В ячейках — число запусков, в которых алгоритм обнаружил страницу с наибольшей конверсией.
Таблица 5
Определение страницы с наибольшей конверсией
|
Алгоритм\Показы |
1000 |
5000 |
10000 |
20000 |
50000 |
|
|
38 |
51 |
53 |
68 |
78 |
|
|
38 |
44 |
58 |
63 |
66 |
|
Softmax(0,01) |
42 |
43 |
42 |
57 |
57 |
|
Pursuit(0.01) |
47 |
50 |
56 |
63 |
55 |
|
UCB1 |
48 |
82 |
90 |
100 |
100 |
Заключение
В данной работе был предложен подход к тестированию интернет-страниц с использованием алгоритмов для решения задачи о многоруком бандите. Были рассмотрены 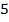 алгоритмов.
алгоритмов.
Предложена программная реализация симуляции процесса тестирования. Результаты работы алгоритмов на некоторых входных данных представлены в работе. Для случая малого числа страниц 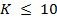 , который рассматривался в работе и который чаще всего и встречается на практике, в ходе многочисленных тестов установлено, что все алгоритмы дают приблизительно равные результаты.
, который рассматривался в работе и который чаще всего и встречается на практике, в ходе многочисленных тестов установлено, что все алгоритмы дают приблизительно равные результаты.
Камнем преткновения к применению алгоритмов является наличие у 4-х из них параметров, которые необходимо подбирать. Общего правила для их подбора, к сожалению, нет. На практике подбор параметра следует осуществлять исходя из его смыслового значения в определенном алгоритме. Кроме того, имея статистические данные, характеризующие конверсию, можно экспериментальным путем подобрать параметры. С точки зрения практического применения среди описанных алгоритмов выгодно отличается алгоритм UCB1, не имеющий параметров. При малом числе показов 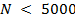 по значению достигнутой конверсии алгоритм уступает другим рассмотренным алгоритмам, однако при увеличении
по значению достигнутой конверсии алгоритм уступает другим рассмотренным алгоритмам, однако при увеличении 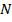 демонстрирует высокий показатель конверсии, сравнимый с другими алгоритмами. Кроме того, благодаря детерминированности алгоритм гарантирует высокую конверсию от запуска к запуску, чего нельзя утверждать о других алгоритмах.
демонстрирует высокий показатель конверсии, сравнимый с другими алгоритмами. Кроме того, благодаря детерминированности алгоритм гарантирует высокую конверсию от запуска к запуску, чего нельзя утверждать о других алгоритмах.
Литература:
1. Жадный алгоритм в A/B-тестировании // URL:http://habrahabr.ru/post/144977/
2. Lai T. L., Robbins H. Asymptotically efficient adaptive allocation rules // Advances in applied mathematics. 1985. No 6. P. 4–22.
3. Sutton R. S., Barto A. G. Introduction to reinforcement learning. MIT Press, 1998.
4. Kuleshov V., Precup D. Algorithms for the multi-armed bandit problem // Journal of Machine Learning Research. 2000. No 1. P. 1–48.
5. Auer P., Cesa-Bianchi N., Fischer P. Finite-time Analysis of the Multiarmed Bandit Problem // Machine Learning. 2002. Vol. 47, No 2–3. P. 235–256
6. Борисова Т. С. Решение задачи исследования-использования для показа баннеров.







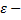 greedy(0,01)
greedy(0,01)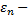 greedy(0,001)
greedy(0,001)