Статья посвящена обоснованиям применения интегрального исчисления к решению ряда экономических задач.
Ключевые слова: определенный интеграл, первообразная,предельные величины, производственная функция, дисконтирование, дисконтирование денежного потока при непрерывном начислении процентов, кривая Лоренца, коэффициент Джини, математическая модель.
Часто размышляя над повышением мотивации к изучению высшей математики на «нематематических» специальностях, понимаю, что четко прослеживается важная роль в этом прикладных задач. Исходя из этого, программу следует строить так, чтобы после знакомства на лекции с новым понятием и после того как студент на практике освоил технику решения примеров с использованием данного понятия, необходимо уделить внимание задачам, непосредственно принадлежащим специализации данной студенческой группы. Нужно, чтобы студенты постоянно чувствовали, что то, чем они занимаются в настоящий момент, близко к их будущей профессии. Важно показать, что огромный спектр этих задач, какая бы разная ни была их постановка, сводится к ограниченному числу различных математических моделей, решать которые ваши студенты уже научились в процессе овладения фундаментальными математическими понятиями. В данной статье я хочу коснуться экономических приложений интеграла.
Приведу несколько экономических понятий и соответствующих им задач, использующих понятие интеграла и иллюстрирующие различные методы интегрирования.
Нахождение экономических функций по известным
предельным величинам
Под предельным (маржинальным) значением показателя в экономическом анализе принято понимать производную функции этого показателя (если эта функция непрерывна). Предельные величины характеризуют процессизменения экономического объекта по времени или относительно некоторого фактора. Они выражают прирост соответствующего показателя в расчете на единицу прироста определяющего его фактора.
В курсе микроэкономики часто приходится находить экономические функции по их известным предельным величинам, т. е. искать саму функцию 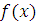 , зная только
, зная только 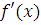 . Поскольку функция
. Поскольку функция 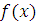 является первообразной функции
является первообразной функции 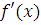 , то нахождение
, то нахождение 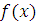 связано с интегрированием функции
связано с интегрированием функции 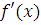 :
: 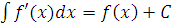 . Таким образом, чтобы найти экономическую функцию по ее предельной, необходимо проинтегрировать предельную функцию.
. Таким образом, чтобы найти экономическую функцию по ее предельной, необходимо проинтегрировать предельную функцию.
Рассмотрим задачу об издержках производства. Издержки производства — это расходы, денежные траты, которые необходимо осуществить для создания единицы товара ([2], c.59), а предельные издержки характеризуют дополнительные затраты на производство единицы дополнительной продукции.
Задача № 1. Задана функция предельных издержек 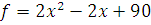 . Найти функцию издержек
. Найти функцию издержек 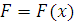 и вычислить издержки на изготовление 15 ед. товара.
и вычислить издержки на изготовление 15 ед. товара.
Решение: При помощи интегрирования находим издержки на изготовления 15 ед. товара 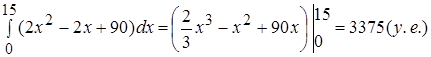 .
.
Функция издержек здесь 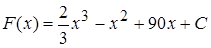 .
.
Нахождение объема продукции по известной функции производительности труда или производственной функции
Пусть функция 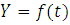 описывает изменения производительности некоторого производства с течением времени. Найдем объем продукции
описывает изменения производительности некоторого производства с течением времени. Найдем объем продукции 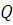 , произведенный за промежуток времени
, произведенный за промежуток времени 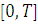 . Разобьем отрезок
. Разобьем отрезок 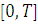 на промежутки времени точками
на промежутки времени точками 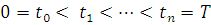 . Выберем на каждом отрезке
. Выберем на каждом отрезке 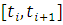 произвольную точку
произвольную точку 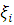 . Тогда объем продукции
. Тогда объем продукции 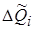 , произведенной за промежуток времени
, произведенной за промежуток времени 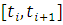 с постоянной производительностью
с постоянной производительностью 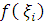 имеет вид:
имеет вид: 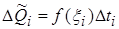 , где
, где 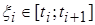 ,
, 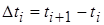 ,
, 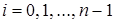 .
.
Обозначим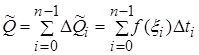 . При
. При 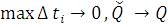 , получаем
, получаем 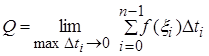 . То есть, по определению определенного интеграла
. То есть, по определению определенного интеграла 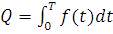 — объем выпускаемой продукции за промежуток
— объем выпускаемой продукции за промежуток 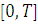 .
.
Задача № 2. Пусть 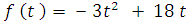 — производительность труда.
— производительность труда.
Определить выработку рабочего:
а) за весь рабочий день;
б) за третий час работы;
в) за последний час работы, если продолжительность рабочего дня 6 часов;
г) провести экономический анализ задачи.
Решение: Находим общую выработку рабочего за весь день (6 часов): 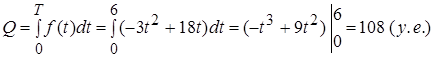 .
.
Определим выработку рабочего за третий час работы: 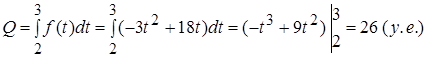
Определим выработку рабочего за последний час работы: 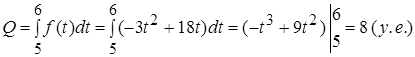
Вероятно, работа утомительна и требует большого напряжения, поэтому к концу дня падает производительность труда.
Производственная функция — это математическое выражение, показывающее зависимость объема производства от количества используемого труда и капитала ([2], c. 55). Наиболее известной производственной функцией является функция Кобба-Дугласа: 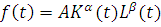 , где
, где 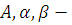 неотрицательные константы,
неотрицательные константы, 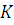 – объем фондов либо в стоимостном, либо в натуральном выражении (скажем число станков),
– объем фондов либо в стоимостном, либо в натуральном выражении (скажем число станков), 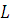 — объем трудовых ресурсов (число рабочих дней, число человеко-дней),
— объем трудовых ресурсов (число рабочих дней, число человеко-дней), 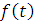 — выпуск продукции в стоимостном, либо в натуральном выражении.
— выпуск продукции в стоимостном, либо в натуральном выражении.
Если в функции Кобба-Дугласа считать, что затраты труда есть линейная зависимость от времени, а затраты капитала 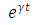 (чтобы поддерживать равновесие между объемом производства выпускаемой продукции и совокупным спросом на нее, скорость денежного потока должна расти со скоростью экспоненты), то она примет вид
(чтобы поддерживать равновесие между объемом производства выпускаемой продукции и совокупным спросом на нее, скорость денежного потока должна расти со скоростью экспоненты), то она примет вид 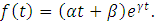 Тогда объем выпускаемой продукции за время
Тогда объем выпускаемой продукции за время 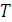 лет составит:
лет составит: 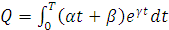 .
.
Задача № 3. Найти объем продукции 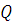 , произведенный за 4 года, если функция Кобба-Дугласа имеет вид:
, произведенный за 4 года, если функция Кобба-Дугласа имеет вид: 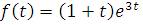 .
.
Решение: Здесь используем для вычисления интеграла метод интегрирования по частям.
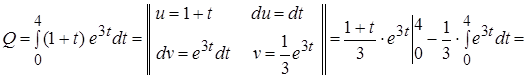
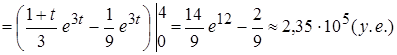 .
.
Среднее время изготовления изделия
Пусть известна функция 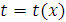 , описывающая изменение затрат времени
, описывающая изменение затрат времени 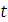 на изготовления изделия, в зависимости от степени освоения производства, где
на изготовления изделия, в зависимости от степени освоения производства, где 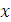 - порядковый номер изделия в партии. Тогда среднее время
- порядковый номер изделия в партии. Тогда среднее время 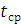 , затраченное на изготовление одного изделия в период от
, затраченное на изготовление одного изделия в период от 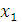 до
до 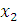 изделий вычисляется по теореме о среднем:
изделий вычисляется по теореме о среднем:
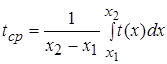 (1)
(1)
Функция изменения затрат времени на изготовление изделий 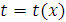 часто имеет вид:
часто имеет вид: 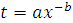 , где
, где 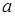 ‒ затраты времени на первое изделие, b ‒ показатель производственного процесса.
‒ затраты времени на первое изделие, b ‒ показатель производственного процесса.
Задача № 4. Найти среднее время, затраченное на освоение одного изделия в период освоения от 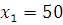 до
до 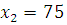 изделий, если функция изменения затрат времени
изделий, если функция изменения затрат времени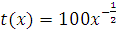 (ч).
(ч).
Решение: Используя формулу (1), получим 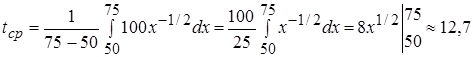 (ч)
(ч)
Дисконтированная стоимость денежного потока
Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность, чем 100 рублей, которые имеются в наличии сегодня. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет.
Определение начальной суммы по ее конечной величине, полученной через время t лет при годовом удельном проценте p, называется дисконтированием ([4], c. 325).
Если вложить 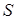 руб. на
руб. на 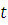 лет под
лет под 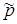 % годовых, то через год сумма будет
% годовых, то через год сумма будет 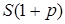 , через 2 года
, через 2 года 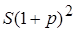 , а через
, а через 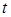 лет
лет 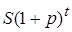 , здесь и везде далее
, здесь и везде далее 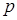 - это процентная ставка, выраженная в долях от единицы (
- это процентная ставка, выраженная в долях от единицы (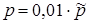 ).
).
Если теперь рассмотреть обратную задачу (задачу дисконтирования), то есть по известной сумме 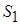 через
через 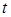 лет определить ее сегодняшнюю стоимость
лет определить ее сегодняшнюю стоимость 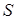 , то из равенства
, то из равенства 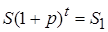 определяя
определяя 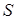 , получим:
, получим:
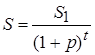 (2)
(2)
Рассмотрим задачу дисконтирования денежного потока, то есть вложение денег будет не единовременным (будем вкладывать деньги, например раз в год в течение всего рассматриваемого периода). Допустим вначале, что для каждого дискретного момента времени 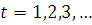 задана величина денежного потока
задана величина денежного потока 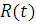 . Если ставку процента обозначить через
. Если ставку процента обозначить через 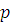 , то дисконтированную стоимость каждой из величин
, то дисконтированную стоимость каждой из величин 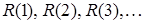 найдем по формуле (2):
найдем по формуле (2): 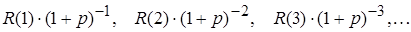 .
.
Тогда дисконтированную стоимость денежного потока найдем, суммируя эти величины
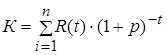 (3)
(3)
здесь 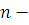 общее число периодов времени.
общее число периодов времени.
А теперь получим формулу дисконтированной стоимости денежного потока при непрерывном начислении процентов. Задачи такого рода встречаются при определении экономической эффективности капиталовложений (долгосрочные, не менее чем на 4 года, денежные вложения или имущественные вклады).
Для этого разобьем рассматриваемый отрезок времени 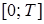 на
на 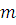 частей. Тогда в каждый промежуток времени удельная процентная ставка будет составлять
частей. Тогда в каждый промежуток времени удельная процентная ставка будет составлять 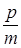 . Устремим
. Устремим 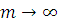 и рассмотрим поведение 2-го множителя в произведении формулы (3):
и рассмотрим поведение 2-го множителя в произведении формулы (3):
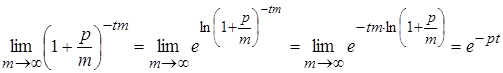 (4)
(4)
Пусть 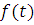 ‒ функция, задающая денежный поток в любой момент времени
‒ функция, задающая денежный поток в любой момент времени 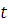 . Тогда, учитывая (2) и (4), дисконтированная стоимость денежных потоков в момент времени
. Тогда, учитывая (2) и (4), дисконтированная стоимость денежных потоков в момент времени 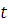 составит
составит
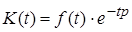 . (5)
. (5)
Заменяя в формуле (3) суммирование интегрированием, получим дисконтированную стоимость денежного потока через 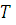 лет при непрерывных процентах:
лет при непрерывных процентах:
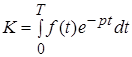 (6)
(6)
Задача № 5. Определить дисконтированный доход за четыре года при процентной ставке 10 %, если первоначальное капиталовложение составило 10 млн. руб. и намечается ежегодно капитал увеличивать на 5 млн. руб. Провести экономический анализ.
Решение: Составим функцию, задающую денежный поток 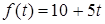 . Тогда дисконтированная сумма капиталовложения вычисляется по формуле (6):
. Тогда дисконтированная сумма капиталовложения вычисляется по формуле (6): 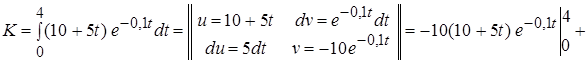
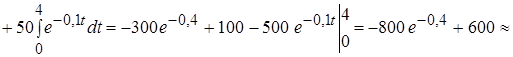
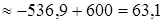 (млн. руб.)
(млн. руб.)
Это означает, что для получения одинаково наращенной суммы через 4 года ежегодные капиталовложения от 10 до 30 млн. руб. равны одновременным первоначальным вложениям 63,1 млн. руб. при той же исчисляемой непрерывной процентной ставке.
Кривая Лоренца. Вычисление коэффициента Джини
Кривая Лоренца ‒ это кривая, отражающая накопленные доли дохода населения ([3], c.412).
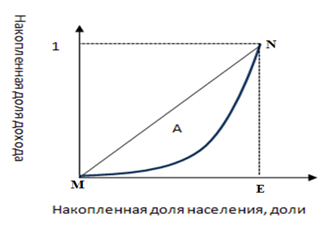
Рис. 1. Кривая Лоренца
В свою очередь, прямая 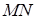 называется линией равномерного распределения доходов. Это гипотетическая линия, которая показывает, что было бы, если доходы в экономике распределялись равномерно. Кривая Лоренца позволяет судить о степени неравенства доходов в экономике по ее изгибу. Для количественного измерения степени неравенства дохода по кривой Лоренца существует специальный коэффициент — коэффициент Джини, который равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника
называется линией равномерного распределения доходов. Это гипотетическая линия, которая показывает, что было бы, если доходы в экономике распределялись равномерно. Кривая Лоренца позволяет судить о степени неравенства доходов в экономике по ее изгибу. Для количественного измерения степени неравенства дохода по кривой Лоренца существует специальный коэффициент — коэффициент Джини, который равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади всего треугольника 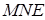 :
:
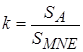
Чем выше неравенство в распределении доходов, тем больше коэффициент 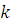 приближается
приближается к единице (абсолютное неравенство). И чем выше равенство в распределении доходов, тем меньше данный коэффициент. При абсолютном равенстве он достигает нуля.
к единице (абсолютное неравенство). И чем выше равенство в распределении доходов, тем меньше данный коэффициент. При абсолютном равенстве он достигает нуля.
Задача № 6. По данным исследования распределения доходов, в одной из стран кривая Лоренца, может быть описана уравнением 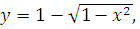 где
где 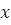 - доля населения,
- доля населения, 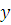 - доля доходов населения. Найти коэффициент Джини.
- доля доходов населения. Найти коэффициент Джини.
Решение: Изобразим заданную кривую (см. рис.2).
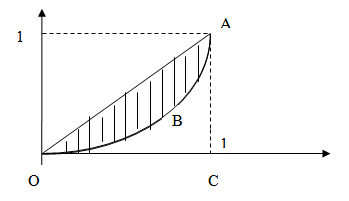
Рис. 2.
Это четверть окружности с центром в точке (0; 1), радиуса 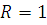 , удовлетворяющая условиям
, удовлетворяющая условиям 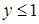 (область изменения функции) и
(область изменения функции) и 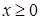 (по смыслу задачи). Проведем также и биссектрису
(по смыслу задачи). Проведем также и биссектрису 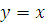 . Тогда коэффициент Джини вычисляется по формуле:
. Тогда коэффициент Джини вычисляется по формуле: 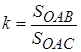 .
.
Вычислим отдельно, 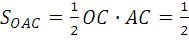 ;
;
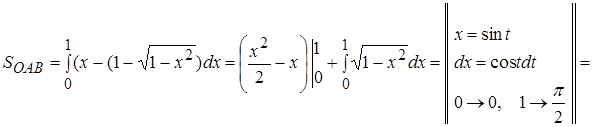
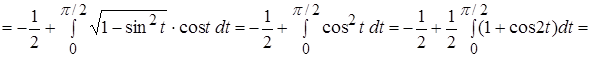
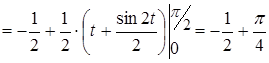 .
.
Тогда коэффициент Джини 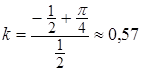 .
.
Высокое значение коэффициента показывает существенное неравномерное распределение доходов среди населения в данной стране.
Литература:
1. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании. 4-е изд., испр. — М.: Дело, 2003. 688 с.
2. Основы экономической теории. Курс лекций. Под редакцией Баскина А. С., Боткина О. И., Ишмановой М. С. Ижевск: Издательский дом «Удмуртский университет», 2000.
3. Нуреев Р. М. Курс микроэкономики: Учебник для вузов.- 2-е изд., изм.-М.: Норма, 2005. 576 с.
4. Солодовников А. С., Бабайцев В. А., Браилов А. В., Шандра И. Г. Математика в экономике: учебник: ч.2. М.: Финансы и статистика. 2007.- 560 с.







