Рассмотрен подход определения температурных профилей и эффективности охлаждения газов в развитом турбулентном барботажном слое на провальных тарелках в колонных аппаратах. Подход базируется на моделях структуры потока для двухфазных сред. Используются диффузионная и ячеечная модели с объемными источниками тепла. Представлены решения уравнений этих моделей для различных частных случаев теплообмена на тарелках. Даны результаты расчетов и сравнение с опытными данными.
Ключевые слова:теплообмен, барботаж, противоток, эффективность, структура потока, законы сохранения.
Введение. На предприятиях нефтегазохимического комплекса и энергетики находят применение пенные аппараты охлаждения газов и жидкостей, которые относятся к теплообменникам смешения. Причем, теплообмен может сопровождаться массообменом или мокрой очистки газов. Наиболее характерные случаи охлаждения газов жидкостями рассмотрены в работах [1,2].
Математическое описание явлений переноса в двухфазных средах с случайным образом распределением дисперсной фазы в сплошной возможно с применением модели многоскоростного континуума или ряда других моделей, которые в итоге приводят к системе уравнений с осредненными источниковыми членами [3, 4].
Законы сохранения в многофазных средах. В дисперсных многофазных системах, встречающихся при осуществлении различных химико-технологических процессов, в сплошной фазе (жидкости или газе) находится значительное количество дисперсных включений — твердых частиц, жидких капель или газовых пузырей. Точное описание движения фаз такой системы на уровне отдельных дисперсных включений представляется невозможным вследствие большого числа этих включений. К тому же точная информация о движении всех дисперсных включений и сплошной фазы между ними является ненужной, так как на практике интерес представляют только некоторые осредненные величины. Поэтому математическое описание осуществляется при помощи осредненных величин.
Обычно предполагается, что такие системы можно изучать, используя представления механики взаимопроникающих взаимодействующих сплошных сред (континуумов). Применение указанных представлений правомерно только в том случае, если для рассматриваемой многофазной системы существует физически бесконечно малый объем. Физически бесконечно малый объем — объем, размеры которого пренебрежимо малы по сравнению с характерным пространственным масштабом макроскопического течения (то есть масштабом, на котором осредненные параметры многофазной среды существенно изменяются). Данное условие позволяет считать, что осредненные по физически бесконечно малому объему характеристики многофазной среды практически постоянны в пределах этого объема. Число дисперсных частиц, заключенных в физически бесконечно малом объеме, должно быть настолько большим, чтобы осредненные по этому объему характеристики многофазной системы были устойчивы по отношению к изменению объема. При этом осредненные по физически бесконечно малому объему величины представляют собой осредненные характеристики фаз реальной многофазной системы. Следовательно, введение физически бесконечно малого объема позволяет представить рассматриваемую многофазную среду как совокупность нескольких (по числу фаз) сплошных сред, обладающих физическими свойствами фаз реальной многофазной среды и непрерывно распределенных в пространстве, занимаемом многофазной средой.
Другое условие, которое обычно предполагается выполненным, заключается в том, что размер неоднородностей в рассматриваемой многофазной системе считается существенно превосходящим молекулярно-кинетические размеры (средние длины свободного пробега молекул, расстояния между молекулами и т. п.), то есть неоднородности содержат очень большое число молекул. Выполнение этого условия позволяет использовать для описания движения отдельных дисперсных включений и окружающей их жидкости (газа) обычные уравнения и методы механики сплошной среды.
Решением таких систем уравнений имеет значительные трудности и при проектировании или модернизации промышленных аппаратов практически используются довольно редко. Авторы данной статьи не раз сталкивались с производственными задачами, когда от технического задания до выдачи технических решений составляет не более месяца, а иногда и несколько дней. В таких случаях наиболее подходят приближенные модели, которые с достаточной для практических целей точностью позволяют быстро получать необходимые результаты. Одной из таких моделей являются модели структуры потока в аппаратах, которые основаны на представлении процесса в аппарате в виде статической системы с различным временем пребывания частиц в потоке.
Диффузионная модель. Наибольшее применение получили двух и однопараметрические диффузионные модели, где все неравномерности распределения фаз учитываются в виде коэффициентов поперечного и обратного (продольного) перемешивания, а так же построенные на их основе комбинированные модели [5,6]. Так, например, при теплопереносе однопараметрическая диффузионная модель структуры потока имеет вид
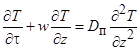 , (1)
, (1)
где 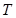 - температура среды;
- температура среды; 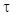 - время, с;
- время, с; 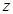 - продольная координата, м;
- продольная координата, м; 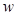 - средняя скорость среды, м/с;
- средняя скорость среды, м/с; 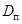 - коэффициент обратного перемешивания, м2/с.
- коэффициент обратного перемешивания, м2/с.
При тепло или массообмене в барботажном слое для учета второй фазы используются объемные источники, уравнения баланса и условия равновесия.
При относительно небольших температурах газов на входе в аппарат (<500) и полным его насыщениями парами воды теплообмен не сопряжен с явлениями испарениями или конденсации и эти эффекты можно не учитывать.
Тогда при стационарном режиме работы провальной барботажной тарелки (рис.1) уравнение (1), записанное для жидкой и газовой фаз с источником теплоты, примет в вид
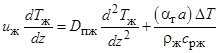 , (2)
, (2)
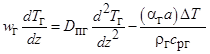 , (3)
, (3)
где 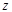 - вертикальная координата по высоте слоя, м;
- вертикальная координата по высоте слоя, м; 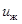 - средняя скорость жидкости, м/с;
- средняя скорость жидкости, м/с; 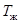 - температура жидкости, 0С;
- температура жидкости, 0С; 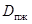 - коэффициент перемешивания по высоте слоя, м2/с;
- коэффициент перемешивания по высоте слоя, м2/с; 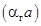 - объемный коэффициент теплоотдачи, Вт/ (м3 К);
- объемный коэффициент теплоотдачи, Вт/ (м3 К); 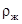 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3; 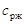 - удельная теплоемкость жидкости, Вт (м К);
- удельная теплоемкость жидкости, Вт (м К); 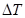 - движущая сила теплопередачи,0С; Источники тепла уравнениях (2) и (3) записаны используя коэффициент теплоотдачи, т. к. известно, что при охлаждении газов основное сопротивление теплопередачи сосредоточено в газовой фазе. Коэффициент теплоотдачи в газовой фазе пенного слоя можно вычислить используя математическую модель [7] или критериальные выражения [1,6]
- движущая сила теплопередачи,0С; Источники тепла уравнениях (2) и (3) записаны используя коэффициент теплоотдачи, т. к. известно, что при охлаждении газов основное сопротивление теплопередачи сосредоточено в газовой фазе. Коэффициент теплоотдачи в газовой фазе пенного слоя можно вычислить используя математическую модель [7] или критериальные выражения [1,6]
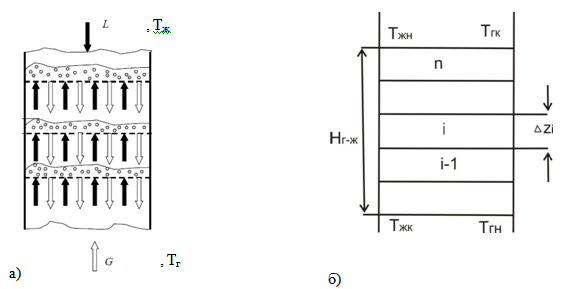
Рис. 1. а) Схема взаимодействия фаз (L,G- массовые расходы жидкости и газа), б) ячеечная модель тарелки
Ячеечная модель. Далее рассмотрим процесс охлаждения газа в пенном слое на провальной тарелке, учитывая, что по газовой фазе практически идеальное вытеснение и поэтому можно использовать ячеечную модель при достаточно большом числе условных ячеек по высоте слоя.
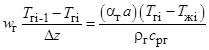 , (4)
, (4)
где i=1,2…, n; n- число ячеек по высоте слоя.
Так как по жидкой фазе происходит практически полное перемешивание запишем уравнение баланса тепла для i-й ячейки
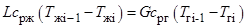 . (5)
. (5)
где L,G — массовые расходы жидкости и газа, кг/с.
Из уравнения теплопереноса (4) и баланса тепла (5) для i-й ячейки получим выражения для расчета профиля температур газа и жидкости в барботажном слое
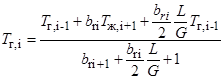 , (6)
, (6)
где 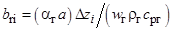 ;
; 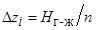 ; где
; где 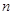 -число ячеек.
-число ячеек.
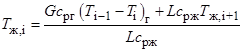 . (7)
. (7)
Температура жидкости на выходе из слоя
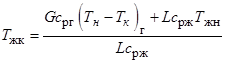 . (8)
. (8)
Тепловая эффективность охлаждения газа
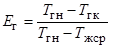 . (9)
. (9)
где 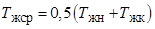 - средняя температура жидкости на тарелке.
- средняя температура жидкости на тарелке.
Примеры расчетов. Примем Тгн=400С; Тжн=200С. В формуле коэффициент bг будет иметь значение bг=1,47. Скорость газа 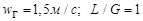 . В результате из расчетов по формуле (6) получим Тгк=280С; а при Тжн=300С, имеем Тгк=34,20С.
. В результате из расчетов по формуле (6) получим Тгк=280С; а при Тжн=300С, имеем Тгк=34,20С.
Температура жидкости на выходе (8) Тжк=23,10С (при Тжн=200С). Тепловая эффективность (9) Ег=0,71(71 %). При начальной температуре Тжн=300С, Тжк=320С. Эффективность Ег=0,72 (72 %). Как и следовало ожидать, тепловой КПД не зависит от значения начальной температуры охлаждающей воды, а определяется гидродинамикой двухфазного слоя.
При идеальном вытеснении по газу тепловую эффективность можно записать по известной формуле
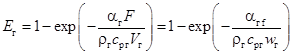 (10)
(10)
или
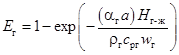 (11)
(11)
где 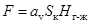 - площадь контакта фаз, м2;
- площадь контакта фаз, м2; 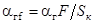 , м/с;
, м/с; 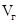 - объемный расход газа, м3/с.
- объемный расход газа, м3/с.
Расчет по формуле (10) дает Ег=0,76 (76 %). Расхождение с расчетами по ячеечной модели составляет 5–6 %, что вполне допустимо для двухфазных сред. Таким образом, если при проектировании пенного теплообменика не требуются знания температурных профилей, то эффективность теплопередачи при охлаждении газа можно вычислить по формуле (10) или (11), которые не требует интернациональных процедур.
На рис. 2 представлено сравнение результатов расчетов тепловой эффективности по формуле (10) с экспериментальными данными [1].
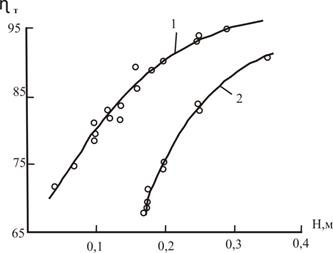
Рис. 2. Зависимость теплового КПД барбатажной тарелки от высоты пены. 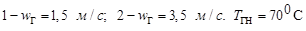 . Точки — эксперимент [1]
. Точки — эксперимент [1]
Расхождение составляет не более 7–8 %.
Представление в статье уравнения можно использовать при проектировании или модернизации пенных теплообменных в различных отраслях промышленности, причем такие задачи могут сопровождаться мокрой очистки газов от пыли [8], флотацией [9] и другими процессами [10].
Литература:
1. Тарат Э. Я. Пенный режим и пенные аппараты / Э. Я. Тарат, И. П. Мухленов, А. Ф. Туболкин, Е. С. Тумаркина. — Л.: Химия, 1977.
2. Лаптев А. Г. Проектирование и модернизация аппаратов разделения в нефте- и газопереработке / А. Г. Лаптев, Н. Г. Минеев, П. А. Мальковский. — Казань: Печатный двор, 2002.
3. Нигматуллин Р. И. Динамика многофазных сред / Р. И. Нигматуллин. — М.: Наука, 1987.
4. D’yakonov S. G., Elizarov V. I., Laptev A. G. Mass transfer model in bubblelayer of contact unit on the basis of active (inlet) section conception. Теорет. основы хим. техн.. 1991. Т. 25. 3 6. С 783–795.
5. Гельперин Н. И. Структура потоков и эффективность колонных аппаратов химической промышленности / Н. И. Гельперин, В. Л. Пебалк, А. Е. Кастанян. — М.: Химия, 1977.
6. Комисссаров Ю. А. и др Процессы и аппараты химической технологии/ Комисссаров Ю. А. и др. Гордеев Л. С., Вент Д. П. -М.: Химия, 2011.-1230с.
7. Лаптев А. Г. Модели пограничного слоя и расчет тепломассообменных процессов / А. Г. Лаптев. — Казань: Изд-во Казанск. ун-та, 2007.
8. Лаптев А. Г., Лаптева Е. А. Модель очистки газов от тонкодисперсной фазы в барботажном слое на основе концепции активного входного участка// Теор. основы хим. технологии, 2015. т. 49. № 2. с.163.
9. Алексеев Д. В., Николаев Н. А., Лаптев А. Г. Комплексная очистка стоков промышленных предприятий методом струйной флотации. Изд-во Казанс. технол. ун-та (КХТИ). 2005.
10. Фарахов М. И., Лаптев А. Г. Энергоэффективное оборудование разделения и очистки веществ в химической технологии. Вестник Казанского технол. ун-та (КХТИ). 2011. № 9. С. 152–158.







