Ключевые слова:деление чисел столбиком, нахождение корня числа, метод Ньютона, школьный курс математики, устные вычисления.
Идея написания данной статьи возникла из тех соображений, что в начале XX века в школах рассказывали об извлечении арифметического квадратного корня из неотрицательного числа в столбик, а в последующем от этого отказались и стали учить только прикидывать, без точных расчетов. Вот и возник вопрос: может быть, нет необходимости учить детей делению в столбик? Может, достаточно учить только приблизительной прикидке?
Сначала расскажем про метод извлечения квадратного корня из чисел. Об этом методе пишет еще сэр Исаак Ньютон (1643–1727 гг) в своей книге «Всеобщая арифметика или книга об арифметических синтезе и анализе» [1, c.35]. Эта книга была переведена на русский язык в 1948 году. Расскажем подробнее о данном методе (по Ньютону).
- Записываем число, из которого требуется извлечь корень, ставим точки над цифрами через одну, начиная с единиц (справа налево);
- Под первой цифрой пишем квадрат числа, меньший данной цифры (При этом найденную цифру записываем отдельно).
- Вычитаем из верхней цифры нижнюю и справа от результата сносим цифры до следующей точки включительно.
- Оставшиеся цифры корня можно последовательно найти посредством деления остатка на удвоенную величину извлеченной части корня и вычитания каждый раз из остатка квадрата последней найденной цифры и ее удесятеренного произведения на названный делитель.
Приведем пример.
Пример 1.Извлечь корень из числа 99856.
Используем метод Ньютона.
- Расставляем точки над цифрами данного числа справа налево через одну.
- Необходимо найти число, квадрат которого равен первой цифре — 9, то есть 3. Записываем цифру 3 в частном и из 9 вычитаем 3×3, то есть 9. Очевидно, в остатке будет 0.
- Рядом с цифрой 0 записываем цифры, предшествующие следующей точке: 98.

Рис. 1. Иллюстрация к примеру 1
- Смотрим, сколько раз удвоенная цифра 3 (то есть 6) содержится в цифре 9. Очевидно, что 1.
- Пишем в частном полученную цифру, т. е. 1.
- Отнимаем от 98 произведение 1×61=61. Получаем 37.
- После 37 сносим оставшиеся цифры — 56, получаем 3756.
- Не обращая внимания на последнюю цифру (то есть 6), смотрим, сколько раз удвоенное число 31 (то есть 62) содержится в числе 375. Очевидно — 6.
- Записываем в частном 6.
- Вычитаем 6×626 = 3756 из числа 3756, получаем в остатке 0.
- Раз получили остаток 0, значит деление закончено, ответом будет число 316.
Интересно заметить, что данный метод с некоторыми изменениями работает и для вычисления кубического корня, корня пятой степени и так далее.
С некоторыми вариациями этот метод довольно долгое время изучался в школах. К примеру, он встречается в учебнике по алгебре для 6–8 классов за 1966 год [2, с.201]. Здесь приводится метод, по которому можно извлечь корень из данного числа с точностью до 1.
Покажем метод так, как он описывается в вышеупомянутом учебнике на примере.
Пример 2. Вычислить корень из числа 4082.
Проведем несложные рассуждения. Это число меньше 10000, значит, его корень будет меньше 100. С другой стороны, это число больше 100, значит, его корень будет больше 10. Получаем число, большее 10 и меньшее 100. В любом таком числе 2 цифры, оно есть десятки + единицы, поэтому квадрат его должен равняться сумме:
(десятки)2 + 2× (единицы) × (десятки) + (десятки)2
Эта сумма должна быть наибольшим квадратом, меньшим, исходного числа. Так как квадрат десятков — это сотни, то квадрат десятков нужно искать в сотнях данного числа. Очевидно, в исходном числе 40 сотен. Наибольший из квадратов чисел, меньший 40 — это 36. Значит, квадрат десятков корня равен 36, тогда число десятков равно 6.
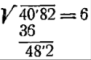
Рис. 2. Иллюстрация 1 к примеру 2.
Записываем цифру 6 справа от знака равенства (см. Рис. 2) — это десятки искомого корня. Возведя цифру 6 в квадрат, получим 36 сотен. Вычитаем 36 сотен из 40 сотен, получаем остаток 4. К нему приписываем оставшиеся цифры — 82. Получили число 482. В этом числе должна содержаться сумма:
2 × (6 десятков) × (единицы) + (единицы)2
Произведение (6 десятков) × (единицы) должно составлять десятки, поэтому удвоенное произведение десятков на единицы будем искать в десятках остатка, а десятки остатка — это 48. Удвоенные десятки корня составляют 12. Тогда, если умножим 12 на единицы корня (пока неизвестные), то должны получить число, содержащееся в 48. Разделим 48 на 12, получим 4. Проверим на правильность эту цифру. Цифра 4 будет верна, если 2(6 десятков)4 + 42 окажется не больше остатка 482.
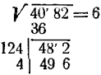
Рис. 3. Иллюстрация 2 к примеру 2.
За вертикальной чертой к удвоенной цифре корня (к 12) приписываем справа цифру 4 и на нее же умножим полученное число (124 на 4) (см. рис. 3).
Проводя умножение, мы умножаем 4 на 4, то есть находим квадрат единиц корня, затем умножаем 12 десятков корня на единицы. В итоге получаем сумму одного и другого. Получили произведение, равное 496, что больше остатка 482, значит, цифра 4 велика и нам не подходит.
Возьмем следующую цифру, меньшую 4, то есть 3. Проведя проверку вышеописанным способом делаем вывод, что цифра 3 подходит. (Если бы она не подошла, мы должны были проверить следующую цифру — цифру 2.)
Напишем найденную цифру 3 справа от цифры десятков. Получили в ответе число 63.
Как мы видим, извлечение корня в столбик — это совсем не сложно, и современные учащиеся даже обычной средней школы смогли бы разобраться в этой теме без особого труда. Но по какой-то причине эта тема давно вычеркнута из тех тем, которые изучают школьники на уроках математики.
Хотя, надо сказать, эта тема присутствует в учебниках математики для детей, увлекающихся математикой, например, в учебнике [3]. Но ведь это все только для увлекающихся математикой детей. А в обычном школьном курсе математики, видимо, эта тема не нужна? Видимо — нет. Хотя ситуация очень спорная.
Отсюда и возник вопрос, поставленный в начале статьи: может быть, тогда и не нужно учить детей делить в столбик? И достаточно, чтобы они могли примерно прикинуть? А остальное сделает калькулятор.
Но ведь, как минимум, калькулятор под рукой далеко не всегда, и что же делать, если нужно точно разделить числа, прикидки недостаточно?
Очевидно, что умение и находить корень числа, и делить числа столбиком очень важно.
Приведем некоторые аргументы в защиту вышесказанного утверждения. И при вычислении корня числа, и при делении чисел используется множество устных подсчетов как минимум в пределах таблицы умножения. А это в свою очередь:
- Способствует повторению и закреплению правил арифметики, что, как показывает практика, актуально для всех учащихся;
- Развивает внимание, самостоятельность, выдержку, смекалку, сообразительность и другие полезные для учащихся качества;
- Тренирует оперативную память детей.
Это далеко не все «плюсы». И это касается абсолютно всех тем математики.
Мы считаем, что чем больше в школьном курсе математики будет разных интересных тем, тем будет лучше.
Также не нужно забывать, что математика в целом и практически любая из ее тем в частности развивает такие способности как:
- Умение обобщать;
- Умение рассуждать и логически мыслить;
- Способность к анализу различных жизненных ситуаций;
- Навык планирования действий и многие другие способности.
Ну и, конечно, не будем забывать высказывание великого русского ученого М. В. Ломоносова: «Математику уже затем учить надо, что она ум в порядок приводит».
Вот для того, чтобы привести ум современных школьников в порядок, и нужно учить их и делению чисел в столбик, и вычислению корня числа, и всему тому, что есть или когда-то было в школьном курсе математики.
Литература:
1. Ньютон И. Всеобщая арифметика, или Книга об арифметических синтезе и анализе.- М.: Издательство Академия Наук СССР, 1948.
2. Барсуков А. Н. Алгебра: учебник для учащихся VI-VIII классов.- М.: Издательство «Просвещение», 1966.
3. Звавич Л. И., Рязановский А. Р. Алгебра. 8 класс. — 5-е изд., перераб. — М.: Мнемозина, 2008.







