DoS-атака — распределенная сетевая атака типа «отказ в обслуживании». Такая атака нарушает нормальное функционирование сетевых устройств и сервисов путем направления большого количества трафика на конкретный узел. Злоумышленник может перехватывать все пакеты, отправляемые определенному адресату.
Важную роль в обеспечении информационной безопасности сети является такой аспект, как доступность (отклик системы на запрос за заданный промежуток времени). Для ее обеспечения требуется вовремя реагировать на резкие скачки входящего трафика. Зачастую сервисы, выполняющие данную функцию, закладываются при проектировании архитектуры системы обработки входящих пакетов.
Целью выполнения работы является анализ метода случайного уничтожения пакетов во входном буфере.
Одной из простейших архитектур является архитектура OQ (Output Queuing). Она состоит из нескольких входных линий и такого же количества обработчиков пакетов, при этом следует учитывать, что каждый обработчик работает со своей входной линией. Данная архитектура не имеет дополнительных средств обеспечения доступности, за исключением расчета устойчивого режима с помощью теории массового обслуживания.
Другим примером является архитектура VOQ (Virtual Output Queuing), предполагающая наличие алгоритма посылки поступающих пакетов обработчикам по циклу [1]. Еще один пример архитектуры, который рассматривается в работах [2,3]: его ключевой особенностью является то, что большая часть трафика (90 %) составляет протокол TCP, и поэтому данная архитектура сосредоточена на контроле только TCP-пакетов.
В данной статье рассматривается моделирование состояния буфера входящих пакетов. В качестве архитектуры выберем FOQ (Feedback Output Queuing), которая описывается в работе [4]. Исходя из названия, архитектура FOQ предполагает обратную связь обработчика пакетов с входным буфером. Обработчики пакетов выполняют следующую функцию: они отслеживают состояние буфера и уничтожают пакеты для предотвращения переполнения.
Постановка задачи
Рассмотрим информационную систему, которая обрабатывает пакеты, поступающие во входной буфер, имеющий длину L. Пусть в систему поступают пакеты с постоянной скоростью u. То есть, в единицу времени в буфер поступает u пакетов. Время примем дискретным, и будем отсчитывать по системному таймеру. Интервал между двумя «тиками» таймера будем считать равным единице. Пусть система обрабатывает поступающие пакеты с постоянной скоростью w пакетов в единицу времени. Обозначив количество пакетов в буфере в момент времени n через xn, можно получить разностное уравнение, описывающее состояние буфера, не используя дополнительные системы уничтожения пакетов.
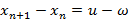
Обозначим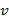 
через 
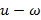. В результате получим рекуррентное соотношение
.
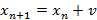В результате данных преобразований задача разбивается на два случая: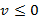 
и
.
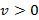Рассмотрим первый случай (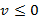). Следует обратить внимание на то, что для любого момента времени n верно неравенство 
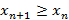. Можно сделать вывод о том, что дополнительные средства очистки буфера не понадобятся, так как скорость обработки пакетов не меньше скорости поступления пакетов (
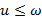), и следовательно, переполнения буфера не возникает.
Во втором случае (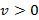), результат прямо противоположен: рост числа пакетов в буфере с течением времени приводит к переполнению буфера. Такой метод нарушения функционирования и нормальной работоспособности информационной системы является ничем иным, как DoS-атакой [5].
Имеется несколько возможных способов защититься от переполнения буфера. Один из методов состоит в том, чтобы уничтожать случайно выбранные пакеты во входном буфере в случае возрастания скорости поступления пакетов. Разумеется, при использовании данного метода имеется вероятность уничтожить и полезные пакеты. Однако на этот случай имеется страховка: при отсутствии ответа на запрос серверы посылают повторный запрос. И следует принять во внимание тот факт, что вероятность случайного уничтожения всех пакетов одного сервера достаточно мала.
Постоянный поток пакетов
Рекуррентное соотношение, рассмотренное выше, для данной модели со случайным уничтожением пакетов преобразуется к виду:
,
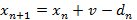где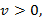 
а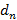 
— количество случайно уничтожаемых пакетов в момент времени n. Случайно уничтожаемые пакеты не обрабатываются.
Важную роль играет выбор последовательности 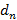, которая зависит от заполнения буфера. Рассмотрим некоторые возможные случаи.
1) 
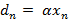— количество уничтожаемых пакетов прямо пропорционально количеству пакетов в буфере (
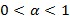). Рекуррентное соотношение преобразуется к виду:
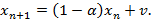
Для решения полученного уравнения необходимо составить соответствующее однородное уравнение. Получим уравнение, описывающее состояние буфера в предыдущий момент времени.
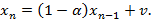
Выразив из данного уравнения v, и подставив его в рекуррентное соотношение, полученное на предыдущем шаге.
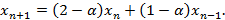
Общее решение данного уравнения будет иметь вид:
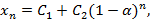
где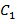 
и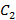 
являются постоянными величинами. Начальное состояние системы - 
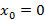. Из последнего рекуррентного соотношения для момента времени n = 1 получим значение 
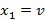. Найдем частное решение данного уравнения, удовлетворяющее заданным условиям:
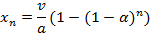
В пределе больших n получаем:
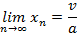
Если для всех моментов времени n выполняется неравенство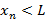 
, то для всех n переполнение буфера происходить не будет, откуда получим условие на коэффициент 
:
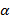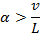
2) 
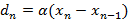— количество уничтожаемых пакетов прямо пропорционально количеству поступающих в буфер пакетов (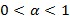). Тогда рекуррентное соотношение преобразуется к виду:
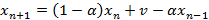
Для решения полученного уравнения необходимо составить соответствующее однородное уравнение. Уравнение, описывающее состояние буфера в предыдущий момент времени будет иметь вид:
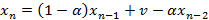
Выразив из него v и подставив его в предыдущее рекуррентное соотношение, получим уравнение:
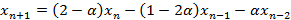
Общее решение данного уравнения имеет вид:
,
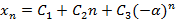где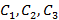 
являются постоянными величинами. Начальное состояние системы -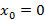. Из последнего рекуррентного соотношения для момента времени 
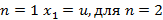получаем значение 
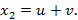Найдем частное решение данного уравнения, удовлетворяющее начальным условиям:
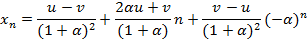
Проанализировав полученное уравнение, можно сделать вывод о том, что величина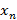 
увеличивается с течением времени. Однако, возрастает она не монотонно из-за наличия слагаемого 
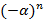. Для любого заданного размера буфера L тем не менее существует момент времени k такой, что 
.
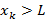Случайный поток пакетов
В случае, когда количество прибывающих пакетов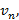 
и соответственно, и количество пакетов в буфере 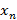являются случайной величиной с гауссовым распределением. Средние значения случайной величины:
,
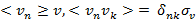где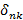 
— символ Кронекера.
Теперь необходимо найти соответствующие средние значения для количества пакетов в буфере. Для этого нужно выбрать количество уничтожаемых пакетов в виде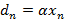 
. В этом случае полученное выше рекуррентное соотношение примет вид:
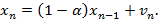
Если это соотношение усреднить по времени, то получим следующее выражение:
.
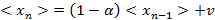В результате получаем выражение:
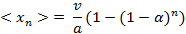
Проанализировав данное выражение, можно сделать вывод, что можно добиться стабильной работы системы без переполнения буфера, как и в случае постоянного потока пакетов, если правильно подобрать коэффициент 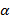. Однако также потребуется оценить дисперсию случайной величины 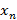, так как если интенсивность поступления пакетов будет случайна, то возможны всплески количества пакетов в буфере. Оценка дисперсии случайной величины :
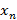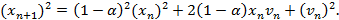
Выразив переменную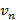 
из рекуррентного соотношения для 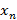, получим следующее выражение:
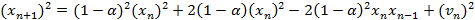
Усреднив это выражение по времени, получим следующее выражение:
.
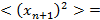
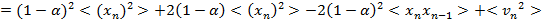Предположим, что 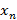имеет гауссово распределение со средними значениями:
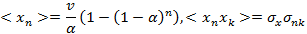
Откуда получим:
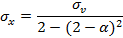
Рассмотрев это выражение, можно сделать вывод о том, что дисперсия наполнения буфера прямо пропорциональна дисперсии интенсивности поступающих пакетов.
Используя правило «трех сигм» из теории вероятности для нормального распределения с вероятностью 0.9973 случайная величина 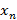будет иметь значения, попадающие в интервал: 
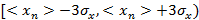. Следовательно, для того, чтобы с вероятностью 0.9973 переполнение буфера не происходило, необходимо, чтобы выполнялось неравенство: 
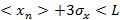. Отсюда получается более строгое неравенство, чем в случае постоянного потока:
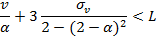
Полученное неравенство можно свести к неравенству третьей степени, которое всегда имеет решение. Экспериментальным путем можно вычислить значения входящего потока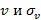 
. Настроить систему можно путем выбора значения коэффициента 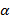. К сожалению, рассмотренные выше соотношения не позволяют вычислить точное оптимальное значение параметра 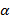, а только определяют его граничные значения.
Заключение
Проведенное исследование показало, что задача построения системы защиты от DoS-атак с помощью метода случайного уничтожения пакетов во входном буфере разрешима. Изменение параметра системы, отвечающего за активность уничтожения пакетов случайным образом, влияет на степень надежности системы. Также следует принимать во внимание тот факт, что активность системы защиты негативно влияет на скорость обработки информации. Но данный недостаток присущ всем системам защиты без исключения, поэтому данным фактом можно пренебречь. Помимо этого следует не забывать, что стопроцентно гарантированной защиты не существует в принципе, и метод случайного уничтожения пакетов во входном буфере не является исключением.
Литература:
1. Nong G., Hamdi M. On the provisioning of Quality of Service guarantees for input queud switches //IEEE Communications Magazine. 2000. V. 38(12). P.62–69.
2. Jacobson V. Congestion avoidance and control //Pro ceeding of ACM SIGCOMM'88.1988. Stanford. P.314–329.
3. Stevens W. TCP slow start, congestion avoidance, fast retransmit, and fast recovery algorithms // IETF RFC 2001, January 1997.
4. Firoiu V., Zhang X., Gunduzhan E., Christin N. Providing service guarantees in high-speed switching systems with feedback output queuing. // arXiv:cs/0406019v1.
5. DDOS атаки [Электронный ресурс] / Режим доступа: http://localname.ru/soft/ataki-tipa-otkaz-v-obsluzhivanii-DoS-i-raspredelennyiy-otkaz-v-obsluzhivanii-dDoS.html
