Вашему вниманию представлен проект роботизированного устройства, которое позволяет произвести скалывание льда в местах, где труд человека опасен для самого человека либо для окружающих, а также позволит производить работы с наибольшей эффективностью и наименьшими затратами. Мы оборудовали робота камерой и пультом управления, благодаря этому оператор может производить управление с безопасной точки. Также данное устройство подразумевает самостоятельный режим, то есть робот способен распознавать льдины и самостоятельно скалывать их без вмешательства и контроля человеком, в результате чего возникает возможность без операторного управления. Кроме того, в своей работе мы рассмотрели манипулятор на точность позиционирования.
Ключевые слова: робот, манипулятор, скалывание льда.
Весна не только дает нам право отдохнуть от суровых холодов недавно прошедшей зимы, но и вносит в жизнь каждого человека элементы «русской рулетки», изо дня в день, выходя из дома, мы не можем быть полностью уверены, что вернемся домой живые и невредимые. И это не из-за опасности на дорогах или нападению хулиганов, а из-за больших шансов попасть под обстрел свисающих с крыш сосулек и съезжающего с откосов снега. Причем каждый год об этом пишется тысячи статей, снимается сотни репортажей, гибнут десятки людей, страдает имущество, однако актуальность данной темы в нашем климате всегда будет велика.
Согласно статистике департамента здравоохранения, с 1 декабря 2014 года по 31 января 2014 от сосулек в городе пострадали восемь человек, а в течение февраля за медпомощью обратились более 40 человек. Только за один день, 24 февраля, от падения сосулек пострадал 21 человек.
В связи с этим нами был разработан проект робота для скалывания льда, который представлен на рис.1, где обозначено: 1- корпус робота; 2-вибромолот; 3-манипулятор; 4- камера; 5- крышка агрегатного отделения; 6- ударник; 7- шасси. При необходимости очистки крыши от снега на робот может быть установлен отвал.
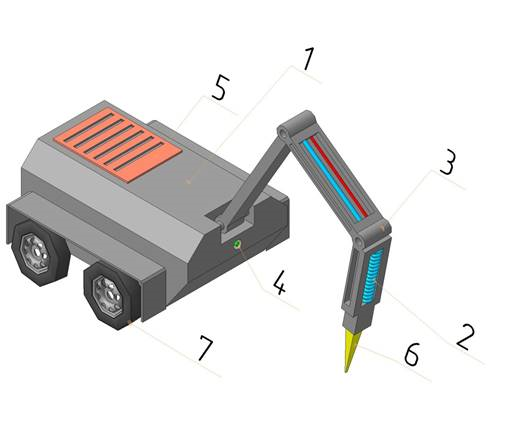
Рис. 1. 3D-модель робота (разработано авторами)
Наша модель имеет небольшие габариты и высокую мощность, а также проходимость, за счет чего скалывает лед с указанного объекта высокопроизводительно при малых затратах. Предусмотрено два режима: безоператорный и операторный. Режим выбирается в зависимости от выбранной задачи. К примеру, если объект просто и легко удаляется, то следует выбирать безоператорный режим, при котором робот самостоятельно выполнит ряд необходимых функций. Если же задача сложная и подъезд к ней затруднен для самостоятельной проходки модели, то необходимо выбрать операторный способ управления роботом. При этом режиме управления пилотирование роботом происходит удаленно с помощью устройства, содержащее специальное программное обеспечение. Это устройство — пульт управления с экраном, на который передается изображение с камеры. Оператор анализирует обстановку и приводит в действие робота и с помощью подвижного рабочего органа выполняет необходимую задачу. При выборе безоператорного режима роботизированное устройство с помощью датчиков, установленных на корпусе робота, определяет размеры ледового покрова и без вмешательства оператора удаляет ледовую глыбу. Из-за высокой мощности, отличной проходимости и большого запаса хода очистка ледовых поверхностей на труднодоступных местах производится быстро, качественно и безопасно. Инновационность подхода заключается в возможность удаленного управления и доступа к роботу в режиме online посредствам установки на робот камеры слежения движения.
В связи со значительной сложностью задачи управления движениями манипуляционного робота ее обычно решают в два этапа: на первом этапе осуществляется планирование траектории, минимизирующей некоторую функцию затрат, а на втором производится отслеживание этой траектории. Ниже рассматривается подход к решению задачи планирования траектории минимальной стоимости при заданной геометрической линии движения манипулятора и ограничениях на величину развиваемых сил (моментов).
Пусть геометрический путь задан параметрической кривой
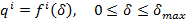 (1)
(1)
где 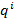 - положение
- положение 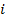 — го сочленения;
— го сочленения; 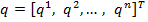 - вектор положения манипулятора с
- вектор положения манипулятора с 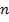 — степенями подвижности; начальная и конечная точки движения соответствуют значениям параметра
— степенями подвижности; начальная и конечная точки движения соответствуют значениям параметра 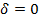 и
и 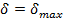 .
.
Будем также полагать, что множество реализуемых моментов (сил), развиваемых приводами, может быть представлено в функции состояния системы (положения и скорости)
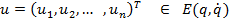 (2)
(2)
На практике обычно желательно ограничить производные вращающих моментов
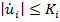 , где
, где 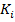 - константа.
- константа.
Уравнения динамики манипулятора можно представить в форме
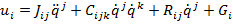 , (3)
, (3)
где 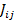 — матрица инерции;
— матрица инерции; 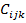 - массив центробежных и кориолисовых коэффициентов;
- массив центробежных и кориолисовых коэффициентов; 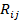 - матрица вязкого трения;
- матрица вязкого трения; 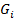 - вектор сил тяжести; используется правило Эйнштейна свертки индексных выражений. Если в уравнение (4) подставить (1), можно получить
- вектор сил тяжести; используется правило Эйнштейна свертки индексных выражений. Если в уравнение (4) подставить (1), можно получить
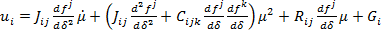 (4)
(4)
где 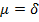 . Будем полгать, что функция стоимости имеет вид
. Будем полгать, что функция стоимости имеет вид
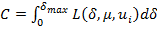 . (5)
. (5)
Тогда требуется найти траекторию, минимизирующую (6) и удовлетворяющую ограничениям (5), (2) и (3).
Рассмотрим подход к решению этой задачи, основанный на использовании динамического программирования. Нанесем на фазовую плоскость 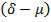 дискретную сетку. Тогда можно вычислить стоимость перехода от одного узла сетки к другому. Перепишем (5) в виде
дискретную сетку. Тогда можно вычислить стоимость перехода от одного узла сетки к другому. Перепишем (5) в виде
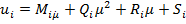 (6)
(6)
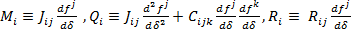 и
и 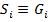 (7)
(7)
Все члены 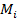 ,
,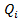 ,
,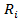 и
и 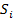 являются функциями
являются функциями 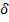 , однако для простоты записи обозначение этой зависимости опущено. Выберем шаг по координате
, однако для простоты записи обозначение этой зависимости опущено. Выберем шаг по координате 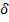 достаточно малым, чтобы функции
достаточно малым, чтобы функции 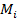 ,
,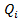 ,
,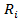 ,
,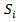 и
и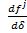 практически не изменялись на единичном интервале. Тогда коэффициенты уравнения (7) можно полагать константами. Проектируя вектор входного момента на вектор скорости
практически не изменялись на единичном интервале. Тогда коэффициенты уравнения (7) можно полагать константами. Проектируя вектор входного момента на вектор скорости 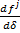 , можно преобразовать (7) к виду
, можно преобразовать (7) к виду
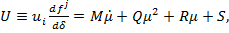 (8)
(8)
где 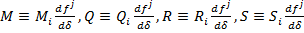 . Разделив (8) на
. Разделив (8) на 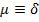 и учитывая, что
и учитывая, что 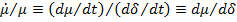 , можно получить
, можно получить
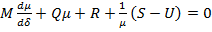 (9)
(9)
Используя (9) как уравнение динамики и учитывая, что в пределах одного интервала дискретизации 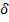 коэффициенты
коэффициенты 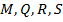 можно полагать константами, найдем решение уравнения (8) с краевыми условиями
можно полагать константами, найдем решение уравнения (8) с краевыми условиями
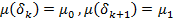 (10)
(10)
на интервале 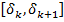 . Будем искать входной момент в форме:
. Будем искать входной момент в форме:
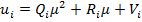
где 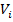 - константы, выбранные таким образом, чтобы удовлетворялись краевые условия (10). Рассмотрим вначале случай, когда отсутствует взаимная зависимость предельных значений моментов, развиваемых в разных степенях подвижности. Тогда множество
- константы, выбранные таким образом, чтобы удовлетворялись краевые условия (10). Рассмотрим вначале случай, когда отсутствует взаимная зависимость предельных значений моментов, развиваемых в разных степенях подвижности. Тогда множество 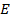 в (2) определяется выражением
в (2) определяется выражением
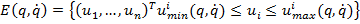 (11)
(11)
Проектируя вектор входного момента в форме (11) на вектор скорости 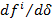 можно получить
можно получить 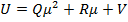 , где
, где 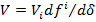 . Подставляя это выражение, в (9) и упрощая, получаем уравнение
. Подставляя это выражение, в (9) и упрощая, получаем уравнение
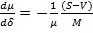 (12)
(12)
Решение уравнения имеет вид
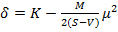 (13)
(13)
Определим константы 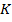 и
и 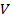 таким образом, чтобы уравнение (14) удовлетворяло краевым условиям (10). Тогда решение имеет вид
таким образом, чтобы уравнение (14) удовлетворяло краевым условиям (10). Тогда решение имеет вид
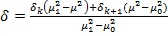 (14)
(14)
Выражая 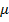 через
через 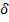 (в [12] показано, что
(в [12] показано, что 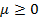 ), можно получить
), можно получить
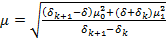 (15)
(15)
Теперь, когда найден путь на одном интервале дискретизации 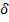 , найдем входы
, найдем входы 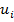 и компоненты приращения функции затрат. Замечая, что
и компоненты приращения функции затрат. Замечая, что 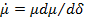 и используя (13), получим
и используя (13), получим
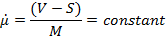
Величины 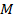 и
и 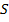 заданы. Выражения (15) и (16) позволяют представить константу
заданы. Выражения (15) и (16) позволяют представить константу 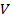 как
как 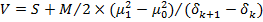 .Используя это выражение для вычисления
.Используя это выражение для вычисления 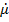 в (16) и подставляя в (7), получим
в (16) и подставляя в (7), получим
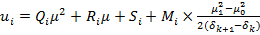 (16)
(16)
Определим, реализуемы ли максимальные и минимальные значения 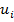 на интервале
на интервале 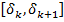 или на соответствующем интервале
или на соответствующем интервале 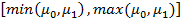 Величина
Величина 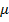 может принимать максимальное или минимальное значение в одной из трех точек интервала:
может принимать максимальное или минимальное значение в одной из трех точек интервала: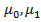 или в точке
или в точке 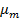 максимального или минимального значения
максимального или минимального значения 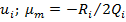 . В случае, если условие
. В случае, если условие
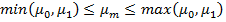 (17)
(17)
не выполняется, управляющие моменты вычисляются только в конечных точках интервала.
Зная скорости и управляющие моменты, можно найти приращение функции затрат
где µ и 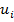 являются функциями
являются функциями 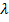 в соотвегствии с (15) и (17), Если интеграл (18) нельзя вычислить аналитически, нужно использовать численные методы.
в соотвегствии с (15) и (17), Если интеграл (18) нельзя вычислить аналитически, нужно использовать численные методы.
Сформулируем основанный на динамическом программировании алгоритм формирования траектории движения. Заданы уравнения динамики манипулятора (5), уравнение кривой (1), ограничения входных моментов (12) и приращение функции стоимости (18). Вначале будем полагать, что производные входных моментов не ограничены. Тогда алгоритм заключается в следующем:
Шаг 1. Определить производные 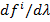 используя эти данные и уравнения динамики манипулятора, найти коэффициенты выражений (7) и (8).
используя эти данные и уравнения динамики манипулятора, найти коэффициенты выражений (7) и (8).
Шаг 2, Дискретизировать фазовую плоскость (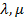 ) путем нанесения прямоугольной сетки, содержащей
) путем нанесения прямоугольной сетки, содержащей 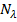 делений по оси
делений по оси 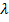 и
и 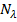 делений по оси р. Сопоставить каждой точке сетки (
делений по оси р. Сопоставить каждой точке сетки (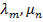 ) величину затрат
) величину затрат 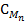 указатель следующей строки Pтп устремить все Стп к бесконечности кроме точки желаемого целевого состояния, в которой затраты устанавливаются равными нулю. Установить все указатели в нулевое состояние и ввести в счетчик столбцов а значение
указатель следующей строки Pтп устремить все Стп к бесконечности кроме точки желаемого целевого состояния, в которой затраты устанавливаются равными нулю. Установить все указатели в нулевое состояние и ввести в счетчик столбцов а значение 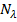
Шаг 3. Если счетчик а показывает нуль, то останов.
Шаг 4. В противном случае установить счетчик текущей строки β в нулевое состояние»
Шаг 5. Если β =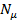 перейти к шагу 12.
перейти к шагу 12.
Шаг 6. В противной случае установить счетчик следующей строки γ в нуль.
Шаг 7. Если 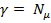 перейти к шагу 11
перейти к шагу 11
Шаг 8. Для, строк 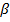 и
и 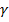 построить кривую, соединяющую точки (a-1,
построить кривую, соединяющую точки (a-1, 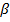 ) и (а,
) и (а,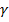 ).Для рассматриваемой линии проверить, удовлетворяют ли, входные моменты ограничениям (12). Если нет, перейти к шагу 10.
).Для рассматриваемой линии проверить, удовлетворяют ли, входные моменты ограничениям (12). Если нет, перейти к шагу 10.
Шаг 9. Вычислить затраты на прохождение участка траектории, прибавляя 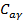 к приращению затрат при переходе от точки (a-1,
к приращению затрат при переходе от точки (a-1, 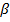 ) к точке (а,
) к точке (а,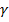 ).Если эта величина меньше, чем
).Если эта величина меньше, чем 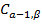 , то присвоить
, то присвоить 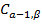 полученное новое значение и установить в указателе
полученное новое значение и установить в указателе 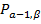 , а значение γ.
, а значение γ.
Шаг 10. Увеличить на единицу содержимое счетчика γ и перейти к шагу 7,
Шаг 11. Увеличить на единицу содержимое счетчика γ и перейти к шагу 5.
Шаг 12, Уменьшить на единицу содержимое счетчика а и перейти к шагу 3.
Последовательность значений, указателя Pтп при переходе из начального в конечное состояние определяет оптимальную траекторию. По полученной оптимальной траектории можно вычислить положения в степенях подвижности, скорости и моменты. [1–11]
Разработанный нами робот позволит произвести скалывание льда в местах, где труд человека опасен для самого человека либо для окружающих, а так же позволит производить работы с наибольшей эффективностью и наименьшими затратами.
Литература:
1. Федотов А. Г., Поезжаева Е. В., Заглядов П. В., Безопасность труда при взаимодействии с промышленными роботами//Экология и научно-технический прогресс. Урбанистика,2014,стр. 14–15.
2. Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 3 ч./ Е. В. Поезжаева. — Пермь Изд-во Пермь.гос, тех. ун-та, 2006.- Ч.1.-64 с.
3. Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 2 ч./ Е. В. Поезжаева. — Пермь Изд-во Пермь.гос, тех. ун-та, 2006.- Ч.1.-64 с.
4. Поезжаева Е. В. Промышленные роботы: учеб.пособие: в 1 ч./ Е. В. Поезжаева. — Пермь Изд-во Пермь.гос, тех. ун-та, 2006.- Ч.1.-64 с.
5. Зенкевич С. Л., Ющенко А:.С. Управление роботами.- М.:Изд-во МГОУ им. Н. Э. Баумана, 2006.
6. Корендясев А. И. Теоретические основы робототехники: в 2 кн./ А. И. Корендясев, Б. Л. Саламандра, Л. И. Тывес; отв. Ред. С. М. Каплунов.– М.:Наука,2006.
7. Хорн Б. К. Зрение роботов.– М.:Мир,1989.
8. Михайлов С. В., Романов В. В., Заикин Д. А., Система технического зрения для диагностики процесса резания материалов//Вестник компьютерных и информационных технологий.,2007,№ 4,стр 23–26
9. Роботизация фермерских хозяйств по обработке растений. Поезжаева Е. В., Васенин А. С., Шумков А. Г. Вестник ВСГУТУ. 2014. № 3 (48). С. 59–62.
10. Робот для тушения отдельных очагов пожара. Поезжаева Е. В., Федотов А. Г., Заглядов П. В. Молодой ученый. 2014. № 16. С. 399–401.
11. Робот-змея для технической диагностики и ремонта трубопроводов. Поезжаева Е. В., Юшков В. С. Новые материалы и технологии в машиностроении. 2011. № 14. С. 93–98.







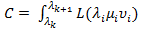 (18)
(18)