Рассмотрена кинематическая модель манипулятора робота, автоматизация разгрузочных операций.
Ключевые слова: манипулятор робот, модель, уравнение.
Необходимость в сокращении времени внутрипроизводственной логистики, вредная для здоровья среда, тяжелый человеческий труд вызывает потребность в автоматизации процессов паллетирования. Скорость и точность работы роботов-паллетайзеров, несравнимы с человеческим трудом, а эффективность и универсальность значительно выше, чем у стандартной машины для паллетирования.
Предприятия легкой и пищевой промышленности заинтересованы в быстрой и качественной упаковке продукции с конвейера. Машины оснащены гибкой рукой-манипулятором, которая позволяет им с ловкостью и осторожностью упаковывать даже самые хрупкие предметы. Робот-упаковщик действует таким образом: просматривает движение конвейера, определив изделие, получает сигнал на электронный блок управления, а тот, в свою очередь, подает команду механической руке взять изделие. Все движения робота совершаются по программе. Это способствует качественному и быстрому процессу упаковки объектов. Целью данной разработки является определение оптимального по быстродействию управления движения схвата манипулятора.
Положение и ориентация рабочего opгана робота зависит от значений обобщенных координат и геометрических параметров, которые задают расстояния и углы поворота между осями шарниров. Реальные значения этих параметров, как правило, отличаются от номинальных значений, что является результатом неточности изготовления или столкновений робота с предметами в процессе эксплуатации. Это приводит к невозможности переноса программ от одного робота к другому (такого же либо иного типа) без перепрограммирования положений, используемых в задании.
Рассмотрим кинематическую модель манипулятора робота, которая представляет собой разомкнутую кинематическую цепь, состоящую из
n+ 1 не деформируемых звеньев. Звенья нумеруем так, что основание имеет номер О, а рабочий орган (схват) имеет номер n. С каждым i -ым звеном жестко связывается координатная система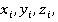 
при этом вектор 
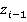направлен вдоль оси i -го шарнира. В соответствии с методом Денавита-Хартенберга взаимное расположение координатных систем определяется значениями параметров 
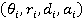(см. рисунок). Шарнирная переменная 
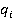равна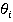 
в случае вращательного сочленения или равна 
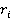. для призматического сочленения.
Пусть i-1Ti — матрица, определяющая координаты системы, связанно с i звеном, по отношению к координатной системе, связанной с i -1 звеном. Можно показать, что
i-1Ti=Rot(z,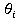
) Trans(z,
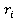) Trans(x,
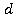)Rot(x,
),
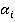где Rot(u,Ѱ)- матрица размером 4x4, угол Ѱ вокруг вектора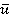 
; Trans(u,l) — матрица размером 4x4, обозначающая перемещение на расстоянии l вдоль вектора .
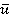Положение и ориентация рабочего органа робота по отношению к опорной координатной системе определяется выражением
W=fTo oTl…n-1Tn=fTn,
где преобразование fTo определяет координаты связанной с основанием системы координат по отношению к опорной системе, которое в свою очередь зависит от четырех констант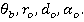 
Положение начала системы координат, связанной с рабочим органом, может быть задано в виде
.
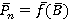Для определения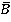 
пользуются линеаризованной моделью, тогда используя достаточное число точек, составляют уравнения, Из этих уравнений методом наименьших квадратов можно определить искомые значения dB.
Вводятся уравнения и, таким образом, определив вектор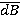 
, можно повысить точность робота за счет использования более точных геометрических параметров при решении обратной кинематической задачи. Справедливо соотношение
,
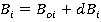которое можно использовать для всех параметров, если обратная кинематическая задача решается с помощью изменяемой кинематической модели робота и имеется возможность подстраивать любой из параметров.
Если обратная кинематическая задача решается с использованием обратной геометрической модели на основе значений параметров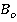 
, то в модели уточняются только следующие параметры:
1) отклонения показаний датчиков;
2) параметры матриц для обратной геометрической модели.
Ошибки положения и ориентации могут быть компенсированы в соответствии с уравнением
,
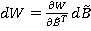где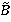 
содержит только параметры, которые не могут быть изменены в модели.
Направлением исследовательской работы является автоматизация разгрузочных операций, разработка специализированного языка программирования, благодаря использованию которого компенсируются ошибки ориентации схвата и увеличивается быстродействие робота.
Литература:
1. Поезжаева Е.В//Теория механизмов и механика систем машин. Промышленные роботы: учеб. пособие: в 3 ч. / Е. В. Поезжаева. — Пермь: Изд-во Перм. Гос. техн. ун-та, 2009.-Ч.2–185.
2. Поезжаева Е.В//Теория механизмов и механика систем машин. Учеб. Пособия/Е. В. Поезжаева.- Пермь: Изд-во Пермского национального исследовательского политехнического университета. 2014.-400
3. Поезжаева Е.В//Теория механизмов и механика систем машин. Промышленные роботы: учеб. пособие: в 3 ч. / Е. В. Поезжаева. — Пермь: Изд-во Перм. Гос. техн. ун-та, 2009.-Ч.3–164.
