Инициирование взрывного разложения композитов на основе бризантных взрывчатых веществ и наночастиц металла импульсом лазера

Предложен критерий инициирования взрывного разложения композитов на основе бризантных взрывчатых веществ и наночастиц металла лазерным импульсом. Им является максимальная температура нагрева, достижение которой не приводит к взрывному разложению. Этот параметр относительно мало зависит от длины волны и длительности импульса, радиуса наночастицы. По аналогии с модельными представлениями теплового взрыва критерий назван температурой вспышки.

Ключевые слова: модель горячей точки, наночастица алюминия, пентаэритриттетранитрат, температура вспышки.

Criterion of the laser pulse initiation of the explosive decomposition of the composites based on high explosives and metal nanoparticles was proposed. It is a maximum heating temperature, while reaching which the composite still does not explode. This parameter almost does not depend on the initiation wavelength, pulse duration, and nanoparticles’ radius. Similarly to the model of the thermal explosion this criterion was called as flash temperature.

Ключевые слова: hot spot model, aluminium nanoparticle, pentraerythritoltetranitrat, flash temperature.

Переход на качественно новый уровень повышения безопасности взрывных работ в горнодобывающей промышленности возможен при использовании оптических детонаторов [1, c. 53]. В последние годы разработан оптический детонатор на основе азида серебра [2, c. 470, 3]. Основной недостаток оптических детонаторов на основе инициирующих взрывчатых веществ определяется их высокой чувствительностью к удару. Одним из современных направлений создания капсюлей оптических детонаторов является введение в существующие бризантные взрывчатые вещества светопоглощающих наночастиц металлов [11, c. 184, 12, c. 39]. В работах [13, c. 102, 14, c. 212] экспериментально показано, что прессованные таблетки пентаэритриттетранитрата (тэн) с добавками наночастиц алюминия, никеля и кобальта проявляют чувствительность к лазерному воздействию на уровне 1 Дж/см². Однако расчет закономерностей взрывного разложения композитов на основе тэна и наночастиц алюминия, кобальта, никеля, золота, серебра, меди, хрома показал, что критическая плотность энергии значительно (в десятки раз) зависит от природы металла и длины волны лазерного импульса. Целью настоящей работы является формулировка критерий инициирования взрывного разложения в рамках микроочаговой модели [15, c. 63].

Микроочаговая модель теплового взрыва была сформулирована для объяснения закономерностей инициирования взрывчатого разложения азидов тяжелых металлов импульсным лазерным излучением [16, c. 14, 17, c. 97]. В модели постулируется, что в энергетическом материале находятся наночастицы, эффективно поглощающие лазерное излучение, и находящиеся в тепловом контакте с матрицей. Очевидным следствием поглощения света наночастицами является быстрое повышение температуры и образование при достаточном нагреве очага теплового взрыва. На скорость и температуру нагревания наночастиц влияет несколько основных факторов: плотность энергии импульса [18, c. 112, 19, c. 195], оптические свойства наночастиц [20, c. 57, 21, c. 7], коэффициенты эффективности поглощения [22, c. 90] и рассеивания света в композите [23, c. 804, 24, c. 751], длина волны инициирующего излучения [25, c. 341, 26 c. 69], фазовые переходы [27, c. 93], длительность импульса. В результате это приводит к значительному различию необходимой для инициирования взрывного разложения плотности энергии импульса. Моделирование процесса взрывного разложения нанокомпозитов приходится вести в условиях существенного различия пространственно-временных характеристик физико-химических процессов. Наиболее эффективным приемом понижения «жесткости» задачи является выделение быстрой подсистемы [28, c. 68, 29, c. 51], имеющей минимальную пространственную локализацию [28, c. 68, 29, c. 51], в данном случае — нагревание одиночной частицы. При этом процессы переноса излучения моделируются отдельно [28, c. 68, 29, c. 51] и определяют единую энергетическую характеристику — эффективную плотность энергии, поглощаемую наночастицей.

Исследование закономерностей низкопорогового инициирования АС импульсом лазера показало, что длительность импульса на полувысоте (τ) является слабым параметром. От него практически не зависят проявления размерных и кинетических эффектов. В недавнем прошлом использовался неодимовый лазер с τ =30 нс [11, c. 68, 12, c. 70, 13, c. 18]. В следующих работах τ сократилось до 20 нс [14, c. 45, 15, c. 63, 16, c. 69], и 12 нс [17, c. 341, 18, c. 38, 19, c. 15]. В работе [4] получено значение длительности импульса на полувысоте 15.5 нс. В данной работе будет проведено исследование взрывного разложения композитов тэн-алюминий при длительности импульса на полувысоте 15.5 нс. Зависимость эволюции физико-химических процессов взрывного разложения системы тэн- наночастицы металла в от длительности импульса будут исследованы в дальнейших работах.

Система дифференциальных уравнений, описывающих процессы кондуктивного теплопереноса в образце, а также тепловыделение за счет химического разложения энергетического материала в сферической симметрии сформулирована в работах [4-10]:

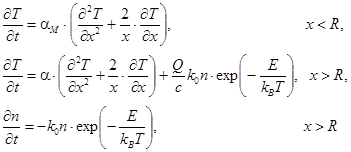                                               (1)

где T — температура, α = 1.1·10–³ см²с^‑1 и α_М= 0.97 см²с^‑1 — коэффициенты температуропроводности тэна и алюминия, x — радиальная координата, Q = 9.64 кДж/см³ — тепловой эффект реакции разложения, n — относительная доля неразложившегося энергетического материала (тэна) (с начальным условием n=1), E = 165 кДж/(моль·K) — энергия активации, k_B — постоянная Больцмана, R — радиус наночастицы, k₀ = 1.2·10¹⁶ с^-1 — предэкспонент, c = 2.22 Дж/(см³·K) и c_М= 2.7 Дж/(см³·K) — объемные теплоемкости тэна и алюминия. Параметры модели, использованы в работе, заимствованы из работ [4-10].

Приток энергии в систему осуществляется за счет поглощения лазерного импульса на поверхности наночастицы. Математически процесс учитывается введением функции J(t), которая определяет поглощаемую наночастицей мощность излучения лазерного импульса в момент времени t. В ранних работах временная форма импульса считалась прямоугольной, для облегчения математических расчетов. В современных лазерных стендах [11, c. 184] зависимость мощности излучения импульса от времени близка к функции нормального распределения:

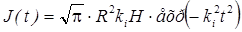,                                                                         (2)

где k_i параметр, определяющий длительность импульса на полувысоте и принимающий значение 1.0743·10⁸ с^-1 при τ = 15.5 нс; Н — поглощаемая наночастицей плотность энергии за импульс. Отличие экспериментального временного профиля импульса и аппроксимируемого выражением (2) составляет менее 5 %, что позволяет использовать выражение (2) для моделирования поглощения лазерного импульса.

Численное решение уравнений модели выполнялось методом конечных разностей на сетке с переменным шагом по координате [22-29]. Рассчитывалась минимальная для данного радиуса наночастицы плотность энергии импульса, инициирующего взрывное разложение (H(R)). Расчет проводился до тех пор, пока минимальная плотность энергии, приводящая к взрыву (H₂), отличалась от максимальной плотности энергии, не приводящей к взрыву (H₁), не более чем на 0.0001 % (1-H₁/ H₂ <0.000001). Ранее считалось, что на данном этапе достаточно точности 10–⁴, она позволяет разделить процессы взрывного разложения и допороговые эффекты. В данной работе точность повышена до 10–⁶.

Затем, используя получившиеся значения H₁, рассчитывалась максимальная температура разогрева вещества с учетом реакции экзотермического разложения и без учета (в системе уравнений значение k₀ присваивалось нулевое значение). Результаты моделирования представлены в таблице 1.

Таблица 1

Рассчитанные в интервале радиусов наночастиц алюминия R =20÷120 нм максимальные значения плотности энергии, при которых взрывной режим не реализуется (H₁), минимальные значения плотности энергии, при которых сисема переходит в самоускоряющийся режим (H₂), значения максимальных температур разогрева при H₁ (T_max1) и значения максимальных температур разогрева при H₁ (T_max2) при k₀ =0.

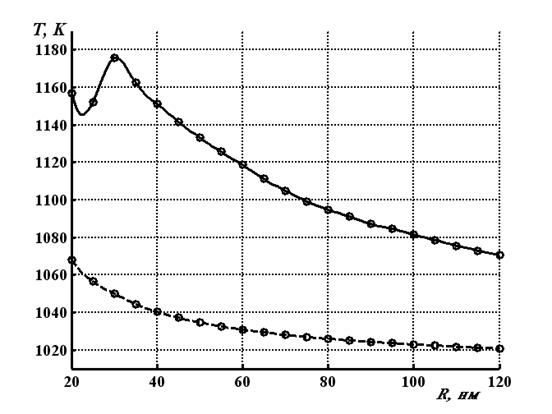
Рис. 1. Рассчитанные зависимости максимальных температур очага реакции, создаваемой наночастицей алюминия в ТЭНе импульсом длительностью 15.5 нс. Сплошная линия — с учетом разогрева за счет химической реакции, пунктирная — при значении k₀=0

Из таблицы 1 видно, что при изменении радиуса наночастиц от 20 нм до 120 нм величины H₁ и H₂ изменяются всего в 1.5 раза, что значительно меньше, чем при учете коэффициента эффективности поглощения. Однако еще более стабильным параметром инициирования взрывного разложения энергетических материалов является необходимая при данной длительности импульса температура перехода реакции в самоускоряющийся режим (аналог температуры вспышки). На рис. 1 представлены рассчитанные зависимости от радиуса наночастицы алюминия максимальной температуры очага реакции, при значении плотности энергии импульса H₁ для каждого радиуса с учетом разогрева за счет энергии химической реакции и без его. Превышение плотности энергии на 0.0001 % приводит к переходу реакции в самоускоряющийся режим. При увеличении размера очага реакции в 6 раз необходимая для перехода реакции в самоускоряющийся режим температура уменьшается на 100 К, но в относительных единицах измерения — всего на 9 %. Поэтому данный параметр можно считать критерием инициирования взрыва при выводе аналитических выражений.

Разница между температурами на рис 1 показывает вклад химической реакции в температуру разогрева. Для наночастиц радиусом 120нм разница составляет 50, для наночастиц 35 нм эта величина уже 118. Из зависимостей представленных на рис. 1 можно сделать вывод, что с уменьшением радиуса наночастицы доля саморазогрева за счет химической реакции увеличивается.

На рис. 1 в районе малых радиусов наночастиц наблюдается понижение температуры в случаи разогрева с учетом химической реакции. Природа экстремальной зависимости, а также эффекты, связанные с изменением длительности импульса будут рассмотрены в дальнейших работах.

Литература:

1.      Ananyeva, M. V. The size effects and before-threshold mode of solid-state chain reaction / M. V. Ananyeva, A. V. Kalenskii // Журнал Сибирского федерального университета. Серия: Химия. — 2014. — Т. 7. — № 4. — С. 470–479.

2.      Боровикова, А. П. Методика моделирования распространения взрывного разложения азида серебра / А. П. Боровикова, А. В. Каленский// Аспирант. — 2014. — № 4. — С. 96–100.

3.      Боровикова, А. П. Пространственно-временные характеристики волны горения в азиде серебра / А. П. Боровикова, А. В. Каленский, И. Ю. Зыков// Аспирант. — 2014. — № 3. — С. 37–42.

4.      Каленский, А. В. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов / А. В. Каленский, А. А. Звеков, М. В. Ананьева и др. // Физика горения и взрыва. — 2014. — Т. 50. — № 3. — С. 98–104.

5.      Kalenskii, A. V. Spectral regularities of the critical energy density of the pentaerythriol tetranitrate -aluminium nanosystems initiated by the laser pulse / A. V. Kalenskii, M. V. Ananyeva // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 6. — С. 803–810.

6.      Никитин, А. П. Расчет критических параметров инициирования теплового взрыва тэна с наночастицами меди на разных длинах волн / А. П. Никитин // Современные фундаментальные и прикладные исследования.– 2013. — № 4(11).– С. 68–75.

7.      Адуев, Б. П. Взрывчатое разложение ТЭНа с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны / Б. П. Адуев, Д. Р. Нурмухаметов, Р. И. Фурега и др. // Химическая физика. — 2013. — Т. 32. — № 8. — С. 39–42.

8.      Ananyeva, M. V. Comparative analysis of energetic materials explosion chain and thermal mechanisms / M. V. Ananyeva, V. G. Kriger, A. V. Kalensii and others // Известия высших учебных заведений. Физика. — 2012. — Т.55. — № 11–3. — С. 13–17.

9.      Каленский, А. В. Взрывная чувствительность композитов тэн-алюминий к действию импульсного лазерного излучения / А. В. Каленский, И. Ю. Зыков, М. В. Ананьева и др. // Вестник КемГУ. — 2014. — № 3–3 (59). — С. 211–217.

10.  Каленский, А. В. Спектральная зависимость критической плотности энергии инициирования композитов на основе пентаэритриттетранитрата с наночастицами никеля / А. В. Каленский, М. В. Ананьева, А. А. Звеков и др.// Фундаментальные проблемы современного материаловедения. — 2014. — Т.11. — № 3. — С. 340–345.

11.  Халиков, Р. М. Технологические схемы решения экологических проблем регионального производства материалов / Р. М. Халиков // Nauka-Rastudent.ru. — 2014. — № 3 (03). — С. 10.

12.  Масленников, Д. А. Столкновение лесного пожара с водным барьером / Д. А. Масленников, Н. А. Лощилова, А. А. Лощилов // Nauka-Rastudent.ru. — 2014. — № 12–1. — С. 42.

13.  Zvekov, A. A. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate — nickel / A. A. Zvekov, M. V. Ananyeva, A. V. Kalenskii and others // Наносистемы: физика, химия, математика. — 2014. — Т. 5. — № 5. — С. 685–691.

14.  Kalenskii, A. V. The Microcenter Heat Explosion Model Modernization / A. V. Kalenskii, V. G. Kriger, A. A. Zvekov and others // Известия ВУЗов. Физика. — 2012. — Т. 55. — № 11/3. — С. 62–65.

15.  Каленский, А. В. Коэффициент захвата электронных носителей заряда на экранированном отталкивающем центре/ А. В. Каленский, М. В. Ананьева, В. Г. Кригер, А. А. Звеков// Химическая физика. — 2014. — Т. 33. — № 4. — С. 11–16.

16.  Кригер, В. Г. Релаксация электронно-возбужденных продуктов твердофазной реакции в кристаллической решетке / В. Г. Кригер, А. В. Каленский, А. А. Звеков // Химическая физика. — 2012. — Т.31. — № 1. — С. 18–22.

17.  Ананьева, М. В. Кинетические закономерности взрывного разложения ТЭНа, содержащего наноразмерные включения алюминия, кобальта и никеля / М. В. Ананьева, А. В. Каленский, Е. А. Гришаева и др. // Вестник КемГУ. — 2014. — № 1–1 (57). — С. 194–200.

18.  Адуев, Б. П. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара / Б. П. Адуев, Д. Р. Нурмухаметов, Г. М. Белокуров и др. // Журнал технической физики. — 2014. — Т. 84. — № 9. — С. 126–131.

19.  Ананьева, М. В. Перспективные составы для капсюля оптического детонатора / М. В. Ананьева, А. А. Звеков, И. Ю. Зыков и др.// Перспективные материалы. — 2014. — № 7. — С. 5–12.

20.  Никитин, А. П. Расчет параметров инициирования взрывного разложения тэна с наночастицами хрома / А. П. Никитин // Современные фундаментальные и прикладные исследования. — 2013. — № 2 (9). — С. 29–34.

21.  Физика взрыва. под ред. Орленко Л. П., М.: Наука, 2004., Т. 1., C. 832.

22.  Адуев, Б. П. Микроочаговая модель лазерного инициирования взрывного разложения энергетических материалов с учетом плавления./ Б. П. Адуев, М. В. Ананьева, А. А. Звеков и др.// Физика горения и взрыва. — 2014. — Т. 50, — № 6. — С. 92–99.

23.  Газенаур, Н. В. Зависимость показателя поглощения меди от длины волны / Н. В. Газенаур, И. Ю. Зыков, А. В. Каленский // Аспирант. — 2014. — № 5. С. 89–93.

24.  Кригер, В. Г. Процессы теплопереноса при лазерном разогреве включений в инертной матрице / В. Г. Кригер, А. В. Каленский, А. А. Звеков и др. // Теплофизика и аэромеханика. — 2013. — Т. 20. — № 3. — С. 375–382.

25.  Ананьева, М. В. Допороговые режимы разветвленных твердофазных цепных реакций / М. В. Ананьева, А. В. Каленский // Актуальные инновационные исследования: наука и практика. — 2014. — № 4. — С. 6.

26.  Звеков, А. А. Моделирование распределения интенсивности в прозрачной среде с Френелевскими границами, содержащей наночастицы алюминия / А. А. Звеков, А. В. Каленский, А. П. Никитин и др.// Компьютерная оптика. — 2014. — Т. 38. — № 4. — С. 749–756.

27.  Каленский, А. В. Расчет коэффициентов эффективности поглощения наночастиц алюминия в прозрачных средах / А. В. Каленский, И. Ю. Зыков, А. П. Никитин // Все материалы. Энциклопедический справочник. — 2015. — № 1. — С. 15–19.

28.  Каленский, А. В. Оптические характеристики наночастиц никеля в прозрачных матрицах / А. В. Каленский, М. В. Ананьева, А. П. Никитин // Современные научные исследования и инновации. — 2014. — № 11–1 (43). — С. 5–13.

29.  Одинцова, О. В. Расчет взрывной чувствительности композитов пентаэритритатетранитрат-серебро к действию лазерного импульса / О. В. Одинцова // Современные фундаментальные и прикладные исследования. — 2014. — № 4 (15). — С. 38–43.