Решается задача об устойчивости сжатой эластомерной пластины в рамках теории тонких пластин и оболочек. Исследуется устойчивость плоской формы равновесия. Бифуркационные равновесные формы строятся с применением численных методов. Теоретические результаты сопоставляются с данными натурного эксперимента.
Ключевые слова: эластомеры, устойчивость, бифуркация, упругий потенциал.
Введение. Одним основоположников нелинейной теории упругости был В. В. Новожилов [45]. В его работах были сформулированы основные положения нелинейной теории упругости, введены понятия физической и геометрической нелинейностей, обоснованы направления исследования упругой потери устойчивости, которой посвящено множество теоретических и экспериментальных работ. Одной из фундаментальных работ, в которой были обобщены полученные к середине двадцатого века результаты исследований, являлась работа А. С. Вольмира [8]. В теоретических исследованиях осуществлялся поиск критических нагрузок и геометрических форм, которые могут реализовываться в закритической области. Основное внимание уделялось исследованию устойчивости пластин и оболочек, материал которых обладает «линейными» физическими свойствами.
Сегодняшние методы решения математических задач позволяют не только дать оценку критических нагрузок, но и построить численные решения нелинейных задач физически и геометрически нелинейной теории упругости [10–13, 15, 16, 20–22, 24, 30–40, 49, 53, 55, 56, 62, 64, 73, 79]. В ряде работ учитывалось и влияние внешних агрессивных сред на напряженно-деформированное состояние упругих тел [50, 52, 54, 75–78, 80, 81]. В среде программирования различных математических пакетов исследовано напряженно-деформирование состояние пластин [23, 51, 65–67, 70–72, 74], оболочек [27–29, 48, 57, 61, 69] и стержней [9, 47, 59, 68] для различных видов физической нелинейности [19, 25, 58, 60, 82]. Одновременно с теоретическими исследованиями разрабатывались и различные методы и алгоритмы построения численных решений нелинейных уравнений в окрестности критических точек [1–5, 7, 14, 17, 18, 26, 41–44, 54, 56, 57, 63, 74, 83]. Наиболее «простой» является задача поиска критической нагрузки для сжатого прямолинейного стержня [8]. Здесь получены значения критических нагрузок при различных вариантах граничных условий с использованием различных подходов. В большинстве исследований для описания механических свойств упругого материала используется закон Гука. Для материалов с нелинейными механическими свойствами картина напряженно-деформированного состояния в задаче о сжатии стержней и пластин может отличаться от результатов, следующих из решения линейной задачи [19, 20, 25, 27, 29, 33]. В работе с позиций нелинейной моментной теории тонких оболочек решается задача поиска критической нагрузки для физически нелинейного упругого материала.
Постановка задачи. Система разрешающих уравнений для плоской бесконечно длинной в одном направлении пластины шириной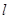 
и толщиной
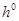, сжимаемой в плоскости нагрузкой с линейной плотностью 
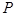, приложенной на крае, имеет вид [22]
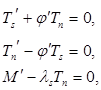(1)
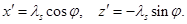
Здесь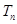 
— перерезывающее усилие, а 
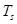— усилие, действующее в меридиональном направлении, 
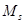— изгибающий момент; 
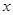и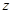 
— координаты точек срединной поверхности, 
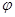— угол между осью 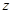и нормалью к срединной поверхности (рис. 1 — распределение усилий в срединной поверхности). Дифференцирование осуществляется вдоль дуги меридиана срединной поверхности (
).
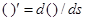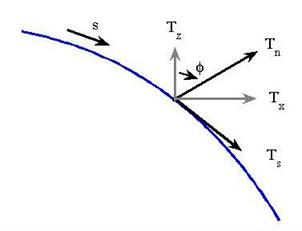
Рис. 1.
Горизонтальное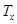 
и вертикальное 
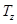усилия подсчитывается по формулам
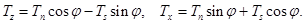
Связь между напряжениями и деформациями определяется с помощью упругого потенциала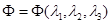 
, являющегося для изотропного материала функцией главных кратностей удлинени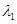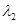й 
, 
и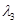 
. Для рассматриваемого случая сжатой пластины 
, 
, 
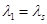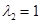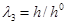, где 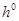— толщина недеформированной пластины, а 
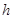— ее толщина в деформированном состоянии. Для случая несжимаемого материала должно выполняться условие несжимаемости 
.
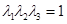В качестве упругого потенциала для несжимаемого материала рассматривается потенциал [25]
,
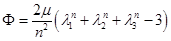в котором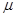 
— «линейный» модуль сдвига, а 
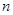— безразмерный параметр. Для этого потенциала с учетом условия несжимаемости [25]
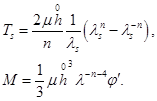(2)
В качестве граничных условий рассматриваются условия шарнирного закрепления пластины на неподвижном крае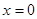 
и горизонтального перемещения края 
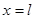под действием нагрузки :
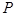при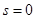 
: , 
, 
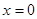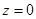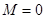, (3)
при 
: 
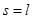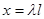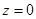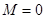, , . (4)
При заданном значении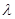 
нагрузка подсчитывается по формуле 
.
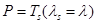Система разрешающих уравнений (1) — (2) при граничных условиях (3) — (4) имеет своим решением
, , 
, , 
, 
, 
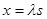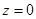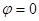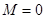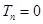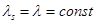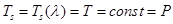. (5)
При этом для сжатой пластины должно выполняться неравенство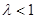 
.
Устойчивость пластины. Пусть наряду решением (5) существует близкое к нему решение
, 
, 
, 
, 
, 
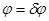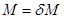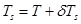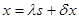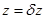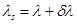
такое, что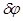 
, 
, 
, 
, , 
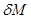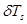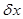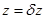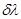— малые величины. Тогда в линейном приближении первые три уравнения в (1) приводятся к виду
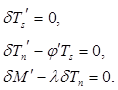(6)
При этом, как это следует из (2),
.
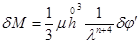С учетом этого из третьего уравнения в (6) следует уравнение для нахождения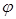 
,
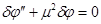где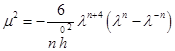 
.
Нетривиальное решение этого уравнение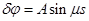 
, удовлетворяющее условиям 
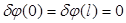, будет существовать при значениях 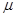, удовлетворяющих условию 
(
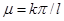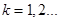) или
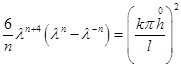. (7)
Левая часть этого уравнения имеет экстремум при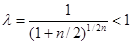 
. Поэтому при достаточно больших значениях 
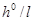уравнение (9) решений иметь не будет.
Для случая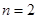 
экстремум достигается при 
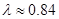и, соответственно, при выполнении неравенства 
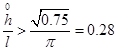линейное приближение системы уравнений (1) будет иметь только тривиальное решение. Таким образом, в рамках рассматриваемой модели сжатая пластина устойчивость может и не терять. Этот результат согласуется с аналогичным результатом, полученным в [28] на основе анализа уравнений нелинейной теории упругости.
Численное решение. Построение решения системы уравнений (1) — (2) с граничными условиями (3) — (4) осуществлялось с применением численных методов. Решение краевой задачи сводилось к решению задачи Коши при заданных на одном крае условиях. Интегрирование дифференциальных уравнений осуществлялось с применением методов типа Рунге-Кутты [17, 46, 61]. Удовлетворение граничным условиям на втором крае осуществлялось методом стрельб.
Некоторые результаты численного решения приведены на рис. 2 в виде зависимости «нагрузка — угол поворота на крае». Кривая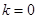 
соответствует прямолинейной равновесной форме, кривая 
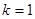— равновесной форме при нагрузках больше первой, но меньше второй критической, 
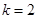— равновесной форме при нагрузках больше второй критической, но меньше третьей. Таким образом, наряду с прямолинейной равновесной формой (рис. 2, 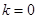) существуют и «изгибные» бифуркационные равновесные формы, «примыкающие» к «прямолинейной». При этом, как показывают численные эксперименты, «координаты» точек бифуркации (критических значений 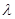) определяются из соотношения (7).
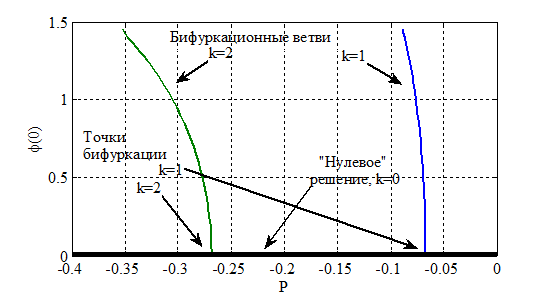
Рис. 2.
Поиск бифуркационных ветвей решений является далеко не простой задачей. В окрестности этих точек системы разрешающих уравнений становятся плохо обусловленными. Как правило, численные методы решения нелинейных дифференциальных уравнений основываются на сведении решения «дифференциальной» задачи к алгебраической [25, 26]. Итерационные методы решения систем нелинейных алгебраических уравнений не обеспечивают сходимость к искомому решению в окрестности таких точек. В этом случае необходима предварительная оценка области существования точек бифуркации с последующим применением специальных методов и алгоритмов построения решения, которые, как правило, не предусмотрены в большинстве математических пакетов. Один из методов, реализованный при решении системы уравнений (1) — (4), состоял в деидеализации исходной системы уравнений [23, 41–44]. Метод основан на представлении о том, что решение неидеальной системы при стремлении к нулю параметров неидеальности стремится к решению идеальной системы [23].
Эксперимент по сжатию прямоугольной пластины. Для сопоставления теоретических результатов с экспериментальными был поставлен эксперимент по осевому сжатию длинной резиновой пластины с поперечными размерами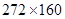 
мм и толщиной 
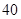мм. Пластина устанавливалась вертикально на металлическую неподвижную платформу, так что один край пластины оставался неподвижным. На втором крае пластины прикладывалась нагрузка по всей ее длине. Сжатие пластины осуществлялось вдоль стороны длинной 
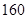мм. Края пластины жестко не закреплялись, что позволило считать ее шарнирно опертой. При малых осадках верхнего края пластины форма пластины была практически прямолинейной. При осадке около 
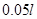пластина резко выпучивалась, что естественно сопоставлялось с потерей устойчивости прямолинейной формы равновесия. В процессе нагружения осуществлялась фотосъёмка деформированной пластины [6, 27]. После обработки фотоматериала строилась форма срединной поверхности. Расчет формы проводился на основе изложенного выше метода. Модуль сдвига 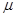определялся из экспериментов по одноосному растяжению образцов [27].
На рис. 3 в системе координат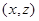 
отображена расчетная форма срединной поверхности (сплошная линия), результаты экспериментальных данных отмечены символом 
.
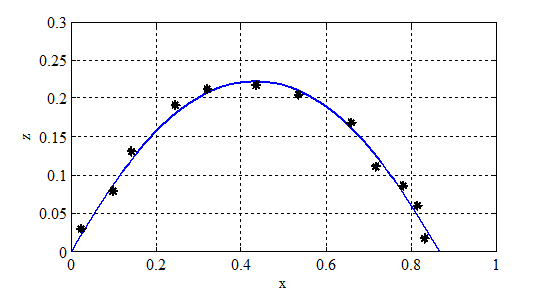
Рис. 3.
В экспериментах реализуется первая «бифуркационная равновесная форма» — изгибная форма в первом приближении представляет собой синусоиду с 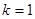в (7).
Заключение. Как следует из результатов исследования учет физической нелинейности материала может привести к результатам отличным от результатов, следующих из линейного варианта закона упругости (закона Гука). Для построения решения в закритической области можно использовать алгоритмы, применяемые при решении задач линейной теории оболочек. Но при этом предварительно необходимо оценить границы области существования решений.
Литература:
1. Атамуратов А. Ж. Исследование подходов к решению задач математической физики на примере уравнения колебаний прямоугольной мембраны // Молодой ученый. — 2013. — № 10. — С. 1–5.
2. Атамуратов А. Ж. Исследование устойчивости двух конечно разностных схем для численного решения уравнения колебаний балки // Молодой ученый. — 2014. — № 1. — С. 1–7.
3. Атамуратов А. Ж. Исследование устойчивости конечно разностных схем для численного решения уравнений колебаний прямоугольной мембраны и прямоугольной пластины // Молодой ученый. — 2014. — № 1. — С. 7–13.
4. Атамуратов А. Ж. Получение интегралов энергии для прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. — 2013. — № 11. — С. 10–15.
5. Атамуратов А. Ж. Приведение к тригонометрической проблеме моментов на примере задачи гашения колебаний прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. — 2013. — № 11. — С. 6–10.
6. Балакина Е. В., Зотов Н. М., Доютов В. А. Общая методика исследования деформаций автомобильной шины с применением фотограмметрии // Молодой ученый. — 2015. — № 6 (86). — С. 120–123.
7. Варыгина М. П. Вычислительный алгоритм для численного моделирования микрополярных упругих ортотропных стержней // Молодой ученый. — 2015. — № 11. — С. 19–22.
8. Вольмир А. С. Устойчивость деформируемых систем. М.: Наука, 1967. — 984 с.
9. Гарькин И. Н., Еркин Д. В. Расчёт стержня с распределенными продольными связями // Молодой ученый. — 2015. — № 5 (85). — С. 124–126.
10. Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
11. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
12. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. № 2. — С. 101–106.
13. Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
14. Голованов А. И., Коноплев Ю. Г., Султанов Л. У. Численное исследование конечных деформаций гиперупругих тел. IV. Конечноэлементная реализация. Примеры решения задач // Ученые записка Казанского университета. — Т. 152. — Кн. 4. — С. 115–126.
15. Даль Ю. М., Пронина Ю. Г Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
16. Даль Ю. М., Пронина Ю. Г. Деформация шаровой поры в нелинейно-упругом теле // Известия Российской академии наук. Серия физическая. — 2006. — Т. 70. — № 9. — С. 1341–1343.
17. Еремин А. С., Олемской И. В. Вложенный метод интегрирования систем структурно разделенных обыкновенных дифференциальных уравнений // Журнал вычислительной математики и математической физики. — 2010. — Т. 50. — № 3. — С. 434–448.
18. Жабко А. П., Екимов А. В., Смирнов Н. В. Анализ асимптотики решения системы интегральных уравнений типа свертки с нормированным ядром // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2000. — № 1. — С. 27.
19. Зубов Л. М., Рудев А. Н. О признаках выполнимости условия Адамара для высокоэластичных материалов // Известия Российской академии наук. Механика твердого тела. — 1994. — № 6. — С. 21.
20. Кабриц С. А. Мальков В. М., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
21. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала // Известия Российской академии наук. Механика твердого тела. — 2001. — № 1. — С. 38.
22. Кабриц С. А., Черных К. Ф. Нелинейная теория изотропно упругих тонких оболочек с учетом поперечного сдвига // Известия Российской академии наук. Механика твердого тела. — 1996. — № 1. — С. 124–136.
23. Кабриц С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2014. — № 2. — С. 261–270.
24. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
25. Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
26. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
27. Колпак Е. П., Мальцева Л. С. Большие деформации резиновых мембран // Молодой ученый. — 2014. — № 16 (75). — С. 78–84.
28. Колпак Е. П., Мальцева Л. С. Круглая плоская мембрана при больших деформациях // Приволжский научный вестник. — 2014. — № 11–1 (39). — С. 5–10.
29. Колтунов М. А., Трояновский И. Е., Шевелев Н. А. Устойчивость толстых упругих пластин с учетом больших деформаций // Механика эластомеров. –1978. — Т. 2. — С. 52–55.
30. Мальков В. М., Кабриц С. А., Мансурова С. Е. Математическое моделирование нелинейной деформации эластомерного слоя // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2011. — № 3. — С. 56–63.
31. Мальков В. М., Малькова Ю. В. Анализ сингулярности напряжений в нелинейной задаче Фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. — С. 652–660.
32. Мальков В. М., Малькова Ю. В. Исследование нелинейной задачи Фламана // Известия Российской академии наук. Механика твердого тела. — 2006. — № 5. — С. 68–78.
33. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
34. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для несжимаемого материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 4. — С. 73–82.
35. Мальков В. М., Малькова Ю. В. Плоская задача нелинейной упругости для гармонического материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 3. — С. 114–126.
36. Мальков В. М., Малькова Ю. В. Плоские задачи о сосредоточенных силах для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 83–96.
37. Мальков В. М., Малькова Ю. В. Плоские задачи упругости для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 3. — С. 93–106.
38. Мальков В. М., Малькова Ю. В. Трещина в форме дуги окружности, расположенная вблизи поверхности раздела материалов // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2010. — № 1. — С. 93–104.
39. Мальков В. М., Малькова Ю. В., Иванов В. А. Бесконечная плоскость с круговым включением, имеющим отслоение на части границы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 4. — С. 152–165.
40. Мальков В. М., Малькова Ю. В., Степанова В. А. Двухкомпонентная плоскость из материала Джона с межфазной трещиной, нагруженной давлением // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2013. — № 3. — С. 113–125.
41. Матросов А. В. Вычислительная неустойчивость алгоритма метода начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 4. — С. 30–39.
42. Матросов А. В. Сходимость степенных рядов в методе начальных функций // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2012. — № 1. — С. 41–51.
43. Матросов А. В. Численно-аналитический расчет балок-стенок на линейно-упругом основании // Вестник государственного университета морского и речного флота им. адмирала С. О. Макарова. — 2011. — № 2. — С. 14a-21.
44. Матросов А. В., Ширунов Г. Н Алгоритмы получения замкнутых форм операторов метода начальных функций для пространственных задач теории упругости // Вестник гражданских инженеров. — 2014. — № 1 (42). — С. 136–144.
45. Новожилов В. В. Основы нелинейной теории упругости. Гостехиздат, 1948. — 212 с.
46. Олемской И. В. Конструирование явных методов типа Рунге-Кутта интегрирования систем специального вида // Известия высших учебных заведений. Математика. — 2005. — № 2. — С. 75–80.
47. Паймушин В. Н. Проблемы геометрической нелинейности и устойчивости в механике тонких оболочек и стержней с прямолинейной осью // Прикладная математика и механика. — 2007. — Т. 71. — № 5. — С. 855–893.
48. Паймушин В. Н., Шалашилин В. И. Уточненные уравнения среднего изгиба трехслойных оболочек и сдвиговые формы потери устойчивости // Доклады Академии наук. — 2003. — Т. 392. — № 2. — С. 195–200.
49. Пронина Ю. Г. Краевая дислокация и сосредоточенная сила в упругой полуплоскости с отверстиями и краевыми вырезами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 4. — С. 120–124.
50. Пронина Ю. Г. Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2006. — № 3. — С. 121–130.
51. Пронина Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
52. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
53. Пронина Ю. Г. Периодическая задача о точечных воздействиях в упругой полуплоскости с отверстиями // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 3. — С. 118–128.
54. Пронина Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129–135.
55. Пронина Ю. Г. Сосредоточенные силы и моменты в упругой полуплоскости с отверстием // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 2. — С. 104–114.
56. Пронина Ю. Г. Центры расширения-сжатия в упругой полуплоскости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 140–149.
57. Решетникова Е. В., Гилева А. Е. Геометрическая нелинейность в задаче расчета напряженно-деформированного состояния оболочек вращения // Молодой ученый. — 2013. — № 12. — С. 168–172.
58. Султанов Л. У., Фахрутдинов Л. Р. Численное исследование гиперупругих материалов // Magazine of Civil Engineering. — 2013. — № 9. — С. 69–74.
59. Чупеев Г. В. Продольно-поперечный изгиб стержней переменного поперечного сечения // Молодой ученый. — 2015. — № 8 (88). — С. 340–344.
60. Agostiniani V., Antonio De Simone D. Ogden-type energies for nematic elastomers // International Journal of Non-Linear Mechanics. — 2012. — V. 47. — 402–412.
61. Bochkareva N. L., Kolpak E. P. On stability of arch damper // Vestnik Sankt-Peterburgskogo Universiteta. Ser 1. Matematika Mekhanika Astronomiya. — 1993. — № 4. — PP. 49–53.
62. Dal' Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
63. Galileev S. M., Matrosov A. V., Verizhenko V. E. Method of initial functions for layered and continuously inhomogeneous plates and shells // Mechanics of Composite Materials. — 1995. — Т. 30. — № 4. — С. 386–392.
64. Gasratova N. A. Study of building an analytical solution of the axisymmetric problem of linear elasticity in stresses as exemplified by finding the stress-strainstate of an ellipsoid cocavityunder the inner pressure // ARPN Journal of Engineering and Applied Sciences. — 2014. — Т. 9. — № 11. — PP. 2259–2267.
65. Kabrits S. A., Kolpak E. P. Numerical Study of Convergence of Nonlinear Models of the Theory of Shells with Thickness Decrease // AIP Conference Proceedings. — 2015. — Т. 1648. — № 300005.
66. Kabrits S. A., Kolpak E. P., Chernykh K. F. Square membrane under large deformations // Mechanics of solids. — 1986. — № 21. — PP. 182–186.
67. Kabrits S. A., Slepneva L. V. Small nonsymmetric oscillations of viscoelastic damper under massive body action // Vestnik Sankt-Peterburgskogo Universiteta. Ser 1. Matematika Mekhanika Astronomiya. — 1998. — № 2. — PP. 78–85.
68. Kabrits S. A., Terent'ev V. F. Numerical solution of one-dimensional nonlinear statics problems for elastic rods and shells in the presence of rigid constraits // Soviet Applied Mechanics. — 1984. — V. 20. — № 7. — PP. 672–675.
69. Kanner L. M., Horgan C. O. Elastic instabilities for strain-stiffening rubber-like spherical and cylindrical thin shells under inflation // International Journal of Non-Linear Mechanics. — 2007. — V. 42. — P. 204–215.
70. Kolesnikov A. M., Zubov L. M. Large bending deformations of a cylindrical membrane with internal pressure // ZAMM Zeitschrift fur Angewandte Mathematik und Mechanik. — 2009. — Т. 89. — № 4. — С. 288–305.
71. Kolpak E. P., Ivanov S. E. Mathematical and computer modeling vibration protection system with damper // Applied Mathematical Sciences. — 2015. — Т. 9. — №. 78. — C. 3875–3885.
72. Kolpak E. P., Kabrits S. A., Bubalo V. The follicle function and thyroid gland cancer // Biology and Medicine. — 2015. — Т. 7 (1). — BM060.15.
73. Malkov V. M., Kabrits S. A. Nonlinear Problems for a layer of low-compressible material // Vestnik Sankt-Peterburgskogo Universiteta. Ser 1. Matematika Mekhanika Astronomiya. — 1999. — № 1. — PP. 86–91.
74. Paǐmushin V. N., Shalashilin V. I. Refined equations of the average bending of three-layer shells and shear forms of stability loss // Doklady Physics. — 2003. — Т. 48. — № 9. — С. 522–527.
75. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
76. Pronina Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. — 2015. — Т. 90. — PP. 161–167.
77. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — C. 361–364.
78. Pronina Y. G. Lifetime assessment for an ideal elastoplastic thick-walled spherical member under general mechanochemical corrosion conditions // Computational Plasticity XII: Fundamentals and Applications — Proceedings of the 12th International Conference on Computational Plasticity — Fundamentals and Applications, COMPLAS 2013. PP. 729–738.
79. Pronina Y. G. Study of possible void nucleation and growth in solids in the framework of the Davis-Nadai deformation theory // Mechanics of Solids. — 2014. — V. 49. — N. 3. — PP. 302–313.
80. Sedova O. S., Khaknazarova L. A., Pronina Y. G. Stress concentration near the corrosion pit on the outer surface of a thick spherical member // 10th International Vacuum Electron Sources Conference, IVESC 2014 and 2nd International Conference on Emission Electronics, ICEE 2014 — Proceedings 6892074.
81. Sedova O., Pronina Y. Generalization of the Lamé problem for three-stage decelerated corrosion process of an elastic hollow sphere // Mechanics Research Communications. — 2015. — V. 65. — PP. 30–34.
82. Wineman A. Some results for generalized neo-Hookean elastic materials // International Journal of Non-Linear Mechanics. — 2005. — V. 40. –P. 271–279.
83. Zhukova I. V., Kolpak E. P., Balykina Yu. E. Mathematical Model of Growing Tumor // Applied Mathematical Sciences. — 2014. — Т. 8. N 29–32. — 1455–1466.
