Для анализа индивидуальных медико-социальных характеристик больных с депрессивными расстройствами целесообразно использование следующих процедур: сравнение медико-социальных характеристик лиц, имеющих диагноз депрессивного расстройства, и пациентов без данной патологии на основе t-критерия Стьюдента и c2 — критерия Пирсона; анализ взаимосвязи исследуемых медико-социальных характеристик на основе вычисления коэффициента парной корреляции Пирсона и коэффициента ранговой корреляции Спирмена; анализ значимости факторов риска развития заболевания; разработка классификационных моделей для выделения лиц с высокой вероятностью развития депрессивных расстройств; разработка моделей для прогнозирования развития заболевания [4, 6, 7, 11].
Ключевые слова: депрессивные расстройства, математическая статистика, прогностическое моделирование, классификационные модели.
Актуальность: Одной из основных предпосылок, обеспечивающих рациональное планирование и управление, является организация интерактивного сбора, поиска, накопления разнородной информации, а также предоставление возможности получения наглядной информации, характеризующей состояние здоровья населения, в реальном масштабе времени, что достигается посредством применения систем мониторинга [1, 8, 15, 19].
При этом мониторинг депрессивных расстройств предлагается рассматривать как многоуровневую систему с выделением регионального (муниципального) и индивидуального уровней [12, 17, 20]. На региональном (муниципальном) уровнях анализируются показатели заболеваемости населения депрессивными расстройствами, деятельности и ресурсного обеспечения учреждений здравоохранения, а на индивидуальном — медико-социальные факторы риска и состояние здоровья больных депрессивными расстройствами [9, 18].
При использовании многоуровневого подхода для системного анализа результатов мониторинга на каждом уровне рассмотрения требуется выбор адекватных методов статистической обработки данных, математического моделирования и принятия решений [21].
Для повышения качества информационной базы для многоуровневого мониторинга и классификационного моделирования, процесс ее формирования должен включать следующие этапы: формирование списка исследуемых показателей, разработка структуры базы данных для мониторинга; проведение сбора фактического материала и заполнение базы данных; преобразование значений качественных характеристик в численные оценки; исключение недостоверных данных (фильтрация информации); заполнение пробелов; оценка информативности и выбор основных контролируемых показателей, отражающих распространенность депрессивных расстройств и состояние здоровья данного контингента населения; разработка интегральных показателей.
Материал и методы исследования. Большую часть информации, на основе которой строятся классификационно-прогностические модели, описывающие распространенность и развитие депрессивных расстройств, собирают при анализе архивной и текущей информации, получении результатов мониторинга, изучении результатов клинических и лабораторных исследований, проведении эксперимента [5]. Показатели, которые измерены в качественной шкале, для дальнейшей статистической обработки требуется преобразовать в количественные оценки. При выполнении сравнения индивидуальных характеристик лиц, вошедших в основную и контрольную группы, для показателей, которые представлены в численном виде применяется t-критерий Стьюдента, а для данных, которые представлены в качественном виде (или в виде таблиц сопряженности) применяется c2-критерий Пирсона [16].
Результаты и их обсуждение. Оценка взаимосвязи медико-социальных характеристик больных с депрессивными расстройствами проводится по значениям коэффициентов парной корреляции. При значении коэффициента парной корреляции от 0 до 0,3 связь оценивалась как «слабая», при значении от 0,3 до 0,7 — связь средней степени, от 0,7 до 1,0 — связь полная. Направление связи оценивали по значению знака, стоящего перед коэффициентом парной корреляции. При значении «+» — связь прямая, при значении «-» — связь обратная. При анализе рассчитанных коэффициентов корреляции учитывались только те, достоверность которых была статистически доказана.
С целью исследования значимости отдельных медико-социальных факторов риска развития депрессивных расстройств выполнялось сравнение показателей основной и контрольной группы по t-критерию Стьюдента. С учетом того, что t-статистика увеличивается при увеличении различия значений показателей в группах сравнения, эта величина была использована в качестве оценки уровня значимости соответствующих изучаемых факторов риска.
С целью оценки влияния индивидуальных характеристик больных депрессивными расстройствами на состояние их здоровья выполнялось вычисление коэффициентов парной корреляции, которые характеризуют силу взаимосвязи исследуемых характеристик с оценкой состояния собственного здоровья больными с депрессивными расстройствами, длительностью лечения, числом и случаев заболеваемости с временной утратой трудоспособности в течение последнего года. На базе полученных данных выполнялось ранжирование индивидуальных медико-социальных характеристик по силе их влияния на ведущие показатели.
Для выделения лиц с высоким риском развития депрессивных расстройств предлагается использовать классификационные модели, позволяющие по набору медико-социальных характеристик отнести вновь поступившего пациента к одной из формализованных групп, соответствующих различным прогнозам развития заболевания [2, 3, 10].
Для прогнозирования состояния больных с депрессивными расстройствами предлагается использовать регрессионные модели, описывающие взаимосвязь показателей, характеризующих состояние здоровья больных с выделенными индивидуальными медико-социальными характеристиками (факторами риска) [13, 14].
Регрессионный анализ дает возможность выявить зависимость, существующую между прогнозируемой величиной и независимыми переменными (одной или несколькими).
В общем виде регрессионная модель имеет следующий вид:
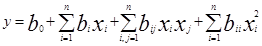
где y — прогнозируемая величина;
xi, xj — индивидуальные характеристики больного;
b0, bi, bij — коэффициенты уравнения регрессии;
n — количество характеристик больного, включенных в модель, отобранных на основе метода «дискретных корреляционных плеяд».
Первоначально обычно строится регрессионная модель, содержащая только линейную комбинацию независимых переменных (линейная модель). Далее проверяется значимость коэффициентов регрессии. Для проверки значимости коэффициентов регрессионного уравнения используется t-критерий Стьюдента:
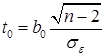 ,
,
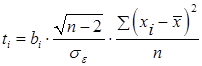 .
.
Определенные по данным выражениям значения t сравниваются с табличными (критическими) их значениями при заданном уровне значимости (обычно α=0,05) и числе степеней свободы k = n-2. Табличные (критические) значения tкр берутся из таблицы распределения Стьюдента.
Коэффициенты, для которых значение t оказалось ниже табличного tкр являются статистически незначимыми и исключаются из уравнения регрессии, а модель перестраивается заново и проверяется ее адекватность с помощью дисперсионного F-критерия (Фишера):
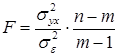 ,
,
где m — число независимых переменных в уравнении регрессии.
Вычисленное значение F сравнивается с табличным (критическим) Fкр для заданного уровня значимости и числа степеней свободы k1 = m-1, k2 = n-m.
Если окажется, что расчетное значение выше критического, считается, что модель адекватно описывает экспериментальные данные, и ее можно использовать для решения практических задач. В противном случае требуется усложнение модели. В этом случае строится модель, учитывающая еще и парные взаимодействия независимых переменных (неполная квадратичная модель), а если и она оказывается не адекватной, то строится полная (квадратичная) модель.
Еще одной эффективной оценкой адекватности построенных моделей, мерой оценки точности аппроксимации эмпирических данных, показателем, характеризующим прогностическую силу анализируемых моделей, является коэффициент детерминации, который определяется по формуле:
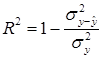 ,
,
где 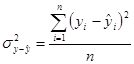 — дисперсия данных, полученных по модели;
— дисперсия данных, полученных по модели;
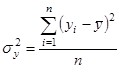 — дисперсия эмпирических данных.
— дисперсия эмпирических данных.
Чем ближе значение R2 к единице, тем точнее модель аппроксимирует эмпирические данные.
Выводы: Таким образом, алгоритм, используемый для построения прогностических моделей на основе регрессионного анализа, включает следующие этапы.
1. На основе экспертного опроса формируется набор индивидуальных медико-социальных характеристик 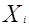
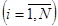 , позволяющих полностью идентифицировать состояние больного с депрессивными расстройствами.
, позволяющих полностью идентифицировать состояние больного с депрессивными расстройствами.
2. Выделяется один или группа прогнозируемых показателей 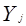
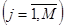 .
.
3. Осуществляется оценка значимости индивидуальных медико-социальных характеристик больных депрессивными расстройствами по степени влияния на состояние здоровья больного.
4. Производится выбор оптимального признакового пространства за счет устранения параметрической избыточности.
5. Выполняется выбор вида регрессионной модели.
6. Осуществляется построение модели с использованием пошагового регрессионного анализа.
7. Выполняется оценка адекватности модели. Если модель адекватна, то переход к окончанию алгоритма. Если построенная модель неадекватна, но имеется возможность ее усложнения, то осуществляется переход к п.4, в противном случае требуется корректировка исходной выборки (использование алгоритмов, направленных на повышение качества информационной базы, увеличение ее объема).
8. Расчет параметров моделей.
Регрессионные модели просты в построении, на их основе появляется возможность исследования зависимости контролируемого показателя от каждого из анализируемых признаков-факторов, включенных в модель.
То есть, на основе построенных моделей возможно «проигрывание» различных вариантов управляющих решений с целью оптимального воздействия на состояние здоровья больных с депрессивными расстройствами.
Литература:
1. Анфилатов В. С. Системный анализ в управлении: Учеб. пособие / В. С. Анфилатов, А. А. Емельянов, А. А. Кукушкин; Под ред. А. А. Емельянова. — М.: Финансы и статистика, 2002. — 368 с.
2. Бурно М. Е. Клиническая психотерапия / М. Е. Бурно. — М.: Деловая книга, 2006. — 800 с.
3. Великанова Л. П. Психосоматические расстройства: Современное состояние проблемы / Л. П. Великанова, Ю. С. Шевченко // Социальная и клиническая психиатрия. — 2005. — Т. 15. Вып. 4. — С. 79–92.
4. Гасников В. К. Методика изучения степени достижения целей здравоохранения на основе системного анализа и экспертных оценок (методические рекомендации). — Ижевск, 1998. — 19 с.
5. Гейслер Е. В. Психиатрия / Е. В. Гейслер, А. А. Дроздов. — М.: ЭКСМО, 2007. — 74 с.
6. Гланц Ст. Медико-биологическая статистика / Пер. с англ; Под ред. Н. Е. Бузинкашвили и Д. В. Самойлова. — М.: Практика 1999.
7. Клименко Г. Я., Есауленко И. Э., Косолапов В. П. и др. Использование балльной оценки для формирования интегрального показателя состояния здоровья населения // Бюллетень НИИ соц. гигиены, экономики и управления здравоохранением им. Н. А. Семашко. — Москва, 2003, с. 18–22.
8. Кореневский Н. А., Дегтярев С. В., Серегин С. П., Новиков А. В.. Интерактивный метод классификации в задачах медицинской диагностики // Медицинская техника. — 2013. — № 4. — С. 1–3.
9. Кузнецова О. Ю.. Профилактика в общей врачебной практике / под ред. О. Ю. Кузнецова, И. С. Глазунова. — СПб.: МАПО, 2004. — 391 с.
10. Куташов В. А., Львович Я. Е., Львович И. Я., Куташова Л. А. Безопасность новых антидепрессантов — селективных ингибиторов обратного захвата серотонина (на примере стимулотона) в комплексной терапии хронических соматических заболеваний // Системный анализ и управление в биомедицинских системах: журнал практической и теоретической биологии и медицины. –2007. — Т. 6, № 4. — С. 804–807.
11. Куташов В. А., А. А. Глухов, Н. А. Степанян, А. И. Рог и др. Статистика в медицинских исследованиях. Монография. Воронеж, 200 с.
12. Куташов В. А., Я. Е. Львович, Постникова И. В. Оптимизация диагностики и терапии аффективных расстройств при хронических заболеваниях. Монография. Воронеж, 2009. — 200 с.
13. Куташов В. А., Будневский А. В., Припутневич Д. Н., Суржко Г. В. Психологические особенности пациентов с последствиями острого нарушения мозгового кровообращения, затрудняющими социальную адаптацию // Вестник неврологии, психиатрии и нейрохирургии. 2014. № 8. С. 8–13.
14. Куташов В. А., Будневский А. В., Припутневич Д. Н., Суржко Г. В. Когнитивные и эмоционально-волевые нарушения у пациентов с последствиями черепно-мозговых травм как фактор нарушения социально-психологической адаптации // Вестник неврологии, психиатрии и нейрохирургии. 2014. № 12. С. 41–45.
15. Куташова Л. А., Куташов В. А., Клименко Г. Я. Оценка диагностической значимости характеристик больных с хроническими заболеваниями для прогнозирования развития депрессивных расстройств // Молодежь и современные информационные технологии: материалы Всерос. молодежной конференции. — Воронеж, 2011. — С. 281–283.
16. Куташова Л. А., Чопоров О. Н., Наумов Н. В., Агарков А. И.. Методы предварительной обработки информации при системном анализе и моделировании медицинских систем // Врач-аспирант. — 2012. — № 6.2 (55). — С. 382–390.
17. Новик А. А. Руководство по исследованию качества жизни в медицине / А. А. Новик, Т. И. Ионова. — М., 2002. — 320 с.
18. Прокудин В. Н. [и др.]. Организация психиатрической помощи в многопрофильной соматической больнице: метод. рекомендации — М., 2003. — 47 с.
19. Родионов О. В., Федорков Е. Д., Фролов В. Н., Фролов М. В.. Управление в биологических и медицинских системах: Учеб. пособие. Под ред. д-ра техн. наук, проф. Я. Е. Львовича. — Воронеж: ВГТУ, 2002. — 342 с.
20. Руководство по профилактике в практическом здравоохранении / Гос. науч.-исслед. центр профилактической медицины МЗ РФ. — М., 2000. — 29 с.
21. Юнкеров В. И. Математико-статистическая обработка данных медицинских исследований / В. И. Юнкеров, С. Г. Григорьев. — СПб.: ВМедА, 2002. — 266 с.







