Обсуждаются основные квантово-механические модели адсорбции на монокристаллических металлических и полупроводниковых подложках и приводится их обобщение на аморфные и поликристаллические материалы.
Ключевые слова: гамильтониан, функция Грина, плотность состояний, аморфный и поликристаллический субстраты.
1. Введение
Незатухающее внимание к изучению адсорбционных явлений обусловлено как практической ценностью получаемых результатов для технических и технологических приложений, так и возможностью получения информации о фундаментальных физико-химических процессах взаимодействия твердого тела с чужеродными атомами. Несомненный интерес представляют исследования влияния молекул (атомов) газа на поверхностные свойства полупроводниковых подложек. Выяснение механизмов такого влияния необходимо, например, для понимания процессов легирования полупроводниковых кристаллов в процессе их роста, пассивации примесей, поверхностной очистки и травления, катализа и разработки полупроводниковых газовых сенсоров. Интенсивные экспериментальные исследования позволили к настоящему времени накопить достаточно обширный экспериментальный материал по целому кругу адсорбционных систем <молекулы (атомы) газа / полупроводниковая подложка>. Для того чтобы правильно ориентироваться в этом массиве данных, необходима теория, позволяющая описать наблюдаемые закономерности. При этом важно понять, каковы те физические механизмы, которые формируют эти зависимости.
Химическая связь (а под адсорбцией мы здесь понимаем именно хемосорбцию), в которой одним из компонентов выступает твердотельная подложка, являющаяся бесконечным резервуаром электронов, является весьма сложной по сравнению с обычной химической связью. Качественная картина возникновения такой связи была предложена Герни еще в 1935 г. Состоит эта картина в следующем. Дискретный уровень первоначально изолированного атома из-за взаимодействия с субстратом сдвигается и уширяется, превращаясь тем самым в квазиуровень [1,2]. Если в сдвинутом состоянии этот квазиуровень перекрывается с зонами разрешенных состояний, то электрон может туннелировать с адатома на подложку и обратно. То же самое относится и к электрону подложки. Такие переходы могут сообщить адатому заряд, превратив его в адион. Главным результатом такой связи является делокализация электрона адатома, ведущая к понижению кинетической энергии электронов адсорбционной системы [1,2]. Такой выигрыш в энергии как раз и определяет так называемую металлическую составляющую энергии адсорбции. Другая составляющая этой энергии называется ионной и представляет из себя, по сути, энергию изображения, т. е. взаимодействию заряда адиона с его изображением в подложке.
Частицу, адсорбированную на поверхности твердого тела, можно рассматривать либо как один из компонентов сложной и весьма специфической «молекулы», либо как примесь, находящуюся в сугубо асимметричном положении относительно других атомов системы. В силу этого, в настоящее время широкое распространение получили три подхода к расчету электронной структуры адатома: квантовохимический кластерный метод, приближение функционала электронной плотности и метод модельных гамильтонианов. Каждый из этих подходов имеет свои преимущества. Первые два, например, позволяют проводить расчеты непосредственно из первых принципов. Кластерный метод, однако, удобен лишь тогда, когда рассматривается адсорбция одиночного атома или малой группы таковых. Наиболее популярный в настоящее время метод функционала плотности требует наличия соответствующего (достаточно сложного) программного обеспечения и мощных компьютеров. С другой стороны, метод модельных гамильтонианов, выделяя лишь наиболее существенные черты исследуемого явления, позволяет получить аналитические выражения для целого ряда характеристик адсорбционной системы. Такой подход наиболее естествен для исследования взаимодействия адатомов, вызывающего изменение электронной структуры адсорбционной системы. Поэтому именно метод модельных гамильтонианов и использовался в настоящей диссертационной работе.
Наиболее популярными гамильтонианами, используемыми в теории адсорбции, являются гамильтонианы Андерсона-Ньюнса и Халдейна-Андерсона [1,2]. Это относится, однако, к адсорбции на упорядоченной (монокристаллической) подложке. Первые обобщения этих моделей на случай разупорядоченной подложки были предприняты, насколько нам известно, авторами этих строк. Здесь дан краткий обзор этих работ.
2. Адсорбция на кристаллических подложках
В настоящее время одним из наиболее популярных подходов в теории адсорбции является метод модельных гамильтонианов [1,2]. Здесь прежде всего стоит отметить гамильтониан Андерсона [3], адаптированный к задаче об адсорбции Ньюнсом [4]. В дираковских обозначениях гамильтониан Андерсона имеет вид
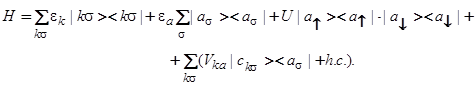 (1)
(1)
Здесь 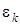 − зонная энергия электрона субстрата, находящегося в состоянии
− зонная энергия электрона субстрата, находящегося в состоянии 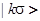 ;
; 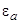 − энергия атомного электрона, находящегося в состоянии
− энергия атомного электрона, находящегося в состоянии 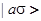 ;
; 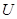 − внутриатомное кулоновское отталкивание электронов с противоположными спинами
− внутриатомное кулоновское отталкивание электронов с противоположными спинами 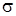 , т. е. находящихся в состояниях
, т. е. находящихся в состояниях 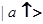 и
и 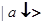 ;
; 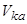 — матричный элемент гибридизации состояний
— матричный элемент гибридизации состояний 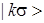 и
и 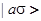 ; h.c. — эрмитово-сопряженные члены. В приближении Хартри — Фока гамильтониану (1) соответствует функция Грина адатома вида [5]
; h.c. — эрмитово-сопряженные члены. В приближении Хартри — Фока гамильтониану (1) соответствует функция Грина адатома вида [5]
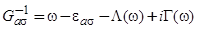 , (2)
, (2)
где
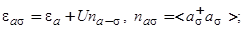 (3)
(3)
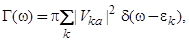 (4)
(4)
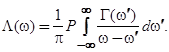 (5)
(5)
В выражениях (2) — (5) под  понимается энергетическая переменная;
понимается энергетическая переменная; 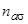 − число заполнения состояния
− число заполнения состояния 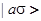 и
и 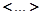 − усреднение по основному состоянию;
− усреднение по основному состоянию; 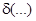 − дельта-функция Дирака; Р — символ главного значения;
− дельта-функция Дирака; Р — символ главного значения; 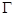 и
и 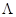 отвечают соответственно полуширине и гибридизационному сдвигу квазиуровня адсорбированного атома (адатома).
отвечают соответственно полуширине и гибридизационному сдвигу квазиуровня адсорбированного атома (адатома).
Будем для простоты считать, что матричный элемент 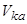 не зависит от квазиволнового вектора
не зависит от квазиволнового вектора 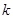 и равен
и равен 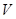 . Тогда вместо (4) получим
. Тогда вместо (4) получим
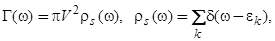 (6)
(6)
где 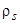 - энергетическая плотность состояний субстрата.
- энергетическая плотность состояний субстрата.
Как в исходной работе Андерсона [1], так и в теории адсорбции на металлах [1,2,5], часто применяется так называемое «приближение широкой зоны», когда можно положить 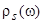 = const. При этом полуширина квазиуровня
= const. При этом полуширина квазиуровня 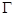 также становиться константой, а сдвиг
также становиться константой, а сдвиг 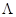 обращается в нуль. В этом случае плотность состояний адатома
обращается в нуль. В этом случае плотность состояний адатома 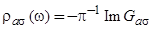 и число заполнения
и число заполнения 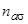 при нулевой температуре принимают простой вид:
при нулевой температуре принимают простой вид:
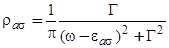 , (7)
, (7)
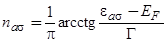 , (8)
, (8)
где 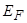 — уровень Ферми адсорбционной системы.
— уровень Ферми адсорбционной системы.
Приближение широкой зоны работает достаточно хорошо, когда уровень адатома 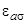 находится вдали от особенностей плотности состояний субстрата
находится вдали от особенностей плотности состояний субстрата 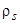 . Таковы, например, случаи адсорбции на простых металлах, характеризующихся достаточно широкой s-зоной. Для переходных металлов это приближение применимо только в том случае, если уровень
. Таковы, например, случаи адсорбции на простых металлах, характеризующихся достаточно широкой s-зоной. Для переходных металлов это приближение применимо только в том случае, если уровень 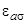 перекрывается с s-зоной и находиться вдали (на расстоянии, значительно превосходящем
перекрывается с s-зоной и находиться вдали (на расстоянии, значительно превосходящем 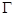 ) от встроенной узкой d-зоны.
) от встроенной узкой d-зоны.
В работах [6–12] было показано, что приближение 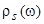 = const может быть применено и к полупроводниковым субстратам. В тех случаях, когда уровень
= const может быть применено и к полупроводниковым субстратам. В тех случаях, когда уровень 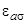 перекрывается с зоной проводимости или валентной (т. е. со сплошным спектром), и находится вдали от краев этих зон, мы, по сути дела, имеем «металлическую ситуацию». Если же уровень
перекрывается с зоной проводимости или валентной (т. е. со сплошным спектром), и находится вдали от краев этих зон, мы, по сути дела, имеем «металлическую ситуацию». Если же уровень 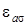 попадает в запрещенную зону и не находиться в резонансе с состояниями примеси, то, в соответствии с (6), функция
попадает в запрещенную зону и не находиться в резонансе с состояниями примеси, то, в соответствии с (6), функция 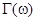 обращается в нуль. Можно, однако, вновь пользоваться выражениями (7) и (8), если переформулировать физический смысл
обращается в нуль. Можно, однако, вновь пользоваться выражениями (7) и (8), если переформулировать физический смысл 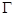 , а именно: считать, что вклад в уширение уровня
, а именно: считать, что вклад в уширение уровня 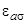 вносят не только процессы туннелирования, но и всевозможные оже-переходы электронов между субстратом и адатомом. Именно таким образом постулируется модельная плотность состояний (7) для атома, адсорбированного на полупроводниковой подложке. При этом, однако, практически исчезает информация о запрещенной зоне субстрата: в формулу (8) входит лишь уровень Ферми системы.
вносят не только процессы туннелирования, но и всевозможные оже-переходы электронов между субстратом и адатомом. Именно таким образом постулируется модельная плотность состояний (7) для атома, адсорбированного на полупроводниковой подложке. При этом, однако, практически исчезает информация о запрещенной зоне субстрата: в формулу (8) входит лишь уровень Ферми системы.
Модель, позволяющая непосредственно учесть наличие запрещенной зоны, была предложена Халдейном и Андерсоном [6] для описания многозарядных примесей в полупроводнике и применена к проблеме адсорбции в работе [13]. В этой модели энергетическая плотность состояний собственного полупроводника 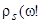 задавалась в виде
задавалась в виде
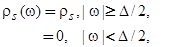 (9)
(9)
где 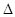 − ширина запрещенной зоны, центр которой принят за начало отсчета энергии,
− ширина запрещенной зоны, центр которой принят за начало отсчета энергии, 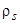 = const. Тогда, в соответствии с (4) и (5), полуширина
= const. Тогда, в соответствии с (4) и (5), полуширина 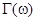 и гибридизационный сдвиг
и гибридизационный сдвиг 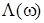 квазиуровня адатома имеют вид
квазиуровня адатома имеют вид
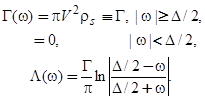 (10)
(10)
Отметим, что при 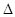 = 0 имеем «металлическую ситуацию»:
= 0 имеем «металлическую ситуацию»: 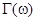 = const,
= const, 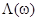 = 0.
= 0.
Возникающие в системе адсорбционные уровни находятся из уравнения
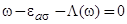 , (11)
, (11)
графическое решение которого представлено на рис.1.
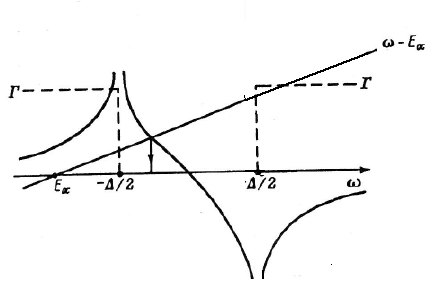
Рис. 1.
Из рис.1 следует, что в адсорбционной системе возникает один локальный уровень 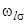 , лежащий в запрещенной зоне, и, возможно, два резонансных
, лежащий в запрещенной зоне, и, возможно, два резонансных 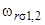 , перекрывающихся с валентной зоной или зоной проводимости. Если уровень
, перекрывающихся с валентной зоной или зоной проводимости. Если уровень 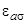 перекрывается с валентной или проводящей зонами, но находится вдали от их краев, резонансных и локальных уровней в действительности может и не существовать, так как в более реалистичной модели расходимости при
перекрывается с валентной или проводящей зонами, но находится вдали от их краев, резонансных и локальных уровней в действительности может и не существовать, так как в более реалистичной модели расходимости при 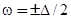 отсутствуют, так как функция
отсутствуют, так как функция 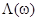 на границах запрещенной зоны имеет конечный максимум. Для локальных состояний
на границах запрещенной зоны имеет конечный максимум. Для локальных состояний 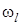 число заполнения
число заполнения 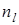 определяется выражением
определяется выражением
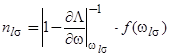 , (12)
, (12)
где мы учли отличную от нуля температуру, введя функцию распределения Ферми-Дирака
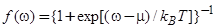 , (13)
, (13)
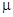 — химический потенциал (при Т = 0 химический потенциал совпадает с уровнем Ферми),
— химический потенциал (при Т = 0 химический потенциал совпадает с уровнем Ферми), 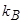 - постоянная Больцмана. Воспользовавшись выражениями (10) и (12), получим
- постоянная Больцмана. Воспользовавшись выражениями (10) и (12), получим
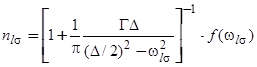 , (14)
, (14)
откуда сразу же следует, что 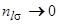 при
при 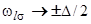 .
.
Вклады в числа заполнения адатома 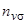 и
и 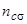 , возникающие из-за взаимодействия состояния адатома
, возникающие из-за взаимодействия состояния адатома 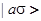 с континуумом состояний валентной зоны и зоны проводимости
с континуумом состояний валентной зоны и зоны проводимости 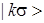 равны соответственно
равны соответственно
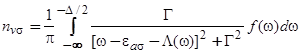 , (15)
, (15)
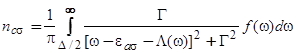 . (16)
. (16)
Суммарное число заполнения адатома
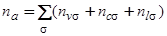 . (17)
. (17)
В дальнейшем будем для простоты считать, что уровень адатома может содержать лишь один электрон. В рамках приближения Хартри-Фока такому случаю отвечает условие 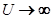 . Поэтому далее спиновый индекс опущен.
. Поэтому далее спиновый индекс опущен.
Обратимся к расчетам чисел заполнения в модели Халдейна — Андерсона. Для начала сделаем некоторые аппроксимации, положив 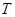 = 0, что сразу же дает
= 0, что сразу же дает 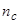 = 0. Легко показать, что влияние температуры на числа заполнения
= 0. Легко показать, что влияние температуры на числа заполнения 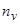 и
и 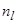 очень слабо, так что аппроксимация
очень слабо, так что аппроксимация 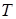 = 0 практически не меняет результаты расчета.
= 0 практически не меняет результаты расчета.
Для вычисления 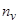 заметим, что величина гибридизационного сдвига
заметим, что величина гибридизационного сдвига 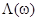 достигает больших значений только в окрестности
достигает больших значений только в окрестности 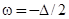 . Эту окрестность можно определить, приравняв в точке
. Эту окрестность можно определить, приравняв в точке 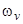 как саму функцию
как саму функцию 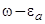 и
и 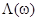 , так и ее производную. Это дает
, так и ее производную. Это дает
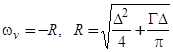 . (18)
. (18)
Если пренебречь вкладом области (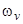 ,
, 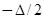 ) в интеграл (15), то приближенно можно положить
) в интеграл (15), то приближенно можно положить
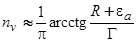 . (19)
. (19)
Сопоставление результатов точных расчетов числа заполнения 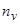 с результатами, полученными с помощью аппроксимации (19) показывает вполне удовлетворительное соответствие. Отметим, что значения чисел заполнения
с результатами, полученными с помощью аппроксимации (19) показывает вполне удовлетворительное соответствие. Отметим, что значения чисел заполнения 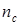 крайне малы (не превосходят 10–5), и вкладом зоны проводимости в число заполнения адатома
крайне малы (не превосходят 10–5), и вкладом зоны проводимости в число заполнения адатома 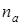 можно пренебречь. Расчеты показывают также, что при
можно пренебречь. Расчеты показывают также, что при 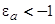 и
и 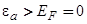 вклад локальных состояний можно не учитывать, так как
вклад локальных состояний можно не учитывать, так как 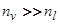 . Следовательно, для таких областей значение
. Следовательно, для таких областей значение 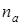 определяется выражением (19).
определяется выражением (19).
Рассмотрим теперь оценки энергии квазиуровня 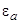 . Если атом до адсорбции содержал на внешнем уровне
. Если атом до адсорбции содержал на внешнем уровне 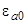 один электрон, то относительно вакуума его энергия равна взятой с отрицательным знаком энергии ионизации
один электрон, то относительно вакуума его энергия равна взятой с отрицательным знаком энергии ионизации 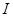 . При приближении к поверхности электрон адатома испытывает отталкивание со стороны электронов подложки. При этом уровень адатома смещается вверх (кулоновский сдвиг), так что уровень
. При приближении к поверхности электрон адатома испытывает отталкивание со стороны электронов подложки. При этом уровень адатома смещается вверх (кулоновский сдвиг), так что уровень 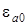 трансформируется в квазиуровень с энергией
трансформируется в квазиуровень с энергией 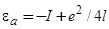 [1], где l — расстояние от центра адатома до плоскости его изображения в подложке, составляющее величину порядка атомного или ионного радиусов адатома (длина адсорбционной связи); е — величина заряда электрона. В этом случае заряд адатома
[1], где l — расстояние от центра адатома до плоскости его изображения в подложке, составляющее величину порядка атомного или ионного радиусов адатома (длина адсорбционной связи); е — величина заряда электрона. В этом случае заряд адатома 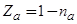 положителен. Это так называемая электроположительная адсорбция. Адатомы при этом отдают электроны, т. е. являются донорами. Если до адсорбции атомный уровень
положителен. Это так называемая электроположительная адсорбция. Адатомы при этом отдают электроны, т. е. являются донорами. Если до адсорбции атомный уровень 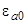 был пуст, то относительно вакуума его энергия равна взятому с обратным знаком сродству к электрону
был пуст, то относительно вакуума его энергия равна взятому с обратным знаком сродству к электрону 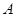 . Вследствие кулоновского притяжения дырки на уровне
. Вследствие кулоновского притяжения дырки на уровне 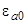 к электронам подложки получаем
к электронам подложки получаем 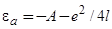 . При этом заряд адатома
. При этом заряд адатома 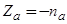 отрицателен; имеем электроотрицательную адсорбцию. В этом случае адатомы выступают как акцепторы.
отрицателен; имеем электроотрицательную адсорбцию. В этом случае адатомы выступают как акцепторы.
При описании адсорбции в приближении Хартри — Фока, когда учитываются оба спиновых состояний электрона на адатоме 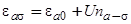 , под энергией
, под энергией 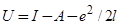 понимают энергию экранированного электронами подложки внутриатомного кулоновского отталкивания [1]. При этом
понимают энергию экранированного электронами подложки внутриатомного кулоновского отталкивания [1]. При этом 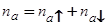 .
.
3. Адсорбция на аморфных подложках
3.1. Модель аморфной подложки
Хорошо известно, что главное отличие аморфного полупроводника от монокристаллического состоит в том, что края зон проводимости и валентной размываются [14–16]. Как следствие, в строгом смысле запрещенная зона в аморфном полупроводнике отсутствует, и можно говорить лишь о щели подвижности. Для описания адсорбции на аморфной подложке модифицируем модель Андерсона — Халдейна.
Вместо выражения (9), зададим плотность состояний полупроводниковой подложки в виде:
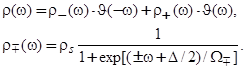 (20)
(20)
Здесь 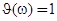 при
при 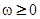 и
и 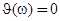 при
при 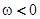 ; нижний индекс «минус» отвечает отрицательным значениям энергии, индекс «плюс» — положительным значениям энергии. За нуль энергии принята середина щели подвижности, в которую переходит запрещенная зона кристаллического полупроводника, занимающая энергетический интервал
; нижний индекс «минус» отвечает отрицательным значениям энергии, индекс «плюс» — положительным значениям энергии. За нуль энергии принята середина щели подвижности, в которую переходит запрещенная зона кристаллического полупроводника, занимающая энергетический интервал 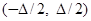 ; параметры
; параметры 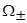 соответствуют характерной энергии размытия верхней (проводящей) и нижней (валентной) зон соответственно;
соответствуют характерной энергии размытия верхней (проводящей) и нижней (валентной) зон соответственно; 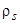 - константа. При
- константа. При 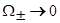 имеем обычную (кристаллическую) модель Халдейна-Андерсона. Плотность состояний при
имеем обычную (кристаллическую) модель Халдейна-Андерсона. Плотность состояний при 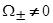 изображена на рис.2 только для положительных значений энергии
изображена на рис.2 только для положительных значений энергии 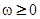 (для
(для 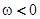 картина зеркально симметрична).
картина зеркально симметрична).
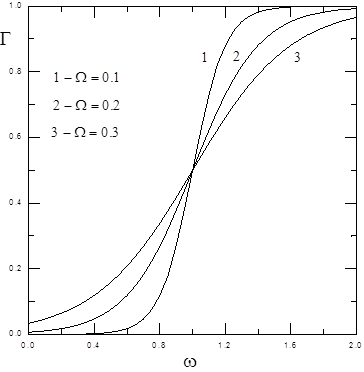
Рис.2.
Введем функции 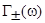 и
и 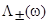 , описывающие, соответственно, уширение и сдвиг атомного уровня:
, описывающие, соответственно, уширение и сдвиг атомного уровня:
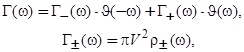 (21)
(21)
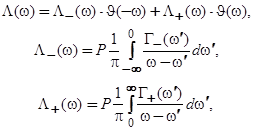 (22)
(22)
где Р — символ главного значения интеграла. Легко показать, что
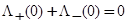 . (23)
. (23)
В дальнейшем для простоты будем считать, что 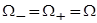 , и рассматривать слабое размытие зон, полагая
, и рассматривать слабое размытие зон, полагая 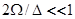 . Тогда можно ввести в модель объединенную плотность состояний
. Тогда можно ввести в модель объединенную плотность состояний
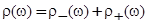 , (24)
, (24)
расширив область определения функций 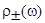 на всю энергетическую ось. Главное отличие представления (24) от (20) заключается в том, что в случае (24) плотность состояний в центре щели подвижности равна
на всю энергетическую ось. Главное отличие представления (24) от (20) заключается в том, что в случае (24) плотность состояний в центре щели подвижности равна
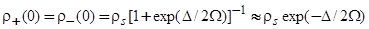 , (25)
, (25)
тогда как в случае (24) имеем в два раза большую величину. Так как мы не занимаемся непосредственно расчетом плотности состояний полупроводника, этим различием можно пренебречь.
Заменяя в (3) знак переменной интегрирования 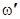 на обратный, получим
на обратный, получим
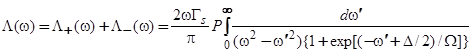 , (26)
, (26)
где 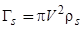 . Из выражения (26), в частности, следует, что функция
. Из выражения (26), в частности, следует, что функция 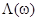 является нечетной, причем
является нечетной, причем 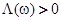 при отрицательных значениях
при отрицательных значениях 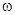 и
и 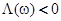 − при положительных. Энергии, возникающие в системе адсорбционных состояний, находятся из следующего уравнения:
− при положительных. Энергии, возникающие в системе адсорбционных состояний, находятся из следующего уравнения:
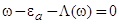 , (27)
, (27)
где 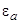 — энергия уровня адсорбируемого атома.
— энергия уровня адсорбируемого атома.
Рассмотрим некоторые аппроксимации для функций 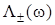 . Из (22) и (23) следует, что главный вклад в интегралы дают значения энергии
. Из (22) и (23) следует, что главный вклад в интегралы дают значения энергии 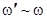 . Тогда в нулевом приближении получим
. Тогда в нулевом приближении получим
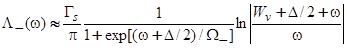 , (28)
, (28)
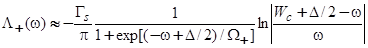 , (29)
, (29)
где 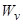 (
(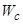 ) — ширина валентной зоны (зоны проводимости). В дальнейшем для простоты будем полагать
) — ширина валентной зоны (зоны проводимости). В дальнейшем для простоты будем полагать 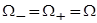 ,
, 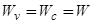 и рассматривать случае слабого размытия зон (
и рассматривать случае слабого размытия зон (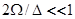 ). Тогда в области потолка валентной зоны, где выполняется неравенство
). Тогда в области потолка валентной зоны, где выполняется неравенство 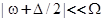 , имеем
, имеем
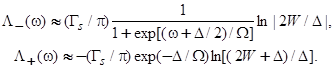 (30)
(30)
Таким образом, в этой области энергий 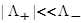 и.
и. 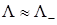 . В окрестности дна зоны проводимости, когда
. В окрестности дна зоны проводимости, когда 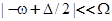 , получим
, получим
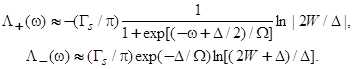 (31)
(31)
Здесь 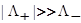 и
и 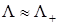 . Вблизи центра щели при
. Вблизи центра щели при 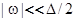 находим
находим
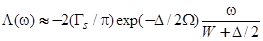 . (32)
. (32)
В дальнейшем будем считать, что 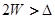 .
.
Теперь рассмотрим «металлический» предел, полагая 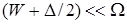 . Тогда легко показать, что при
. Тогда легко показать, что при 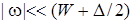
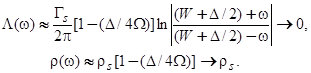 (33)
(33)
Полученные выражения совпадают с результатами модели Андерсона-Ньюнса.
3.2. Адсорбция на аморфной подложке
Перейдем теперь к рассмотрению адсорбции. Начнем с частного случая, когда 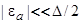 . Из уравнения (27) с учетом (32) найдем положение резонансного уровня
. Из уравнения (27) с учетом (32) найдем положение резонансного уровня 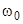 :
:
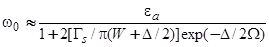 . (34)
. (34)
Как следует из формулы (25), в области энергий 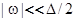 значение
значение
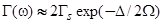 . (35)
. (35)
Плотность состояний на адатоме 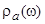 и его число заполнения
и его число заполнения 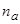 могут быть представлены в виде:
могут быть представлены в виде:
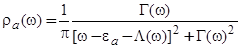 , (36)
, (36)
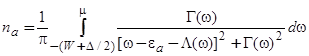 , (37)
, (37)
где 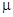 — химический потенциал. В области энергий
— химический потенциал. В области энергий 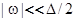 плотность состояний
плотность состояний 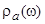 можно представить в виде
можно представить в виде
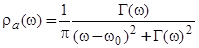 , (38)
, (38)
где 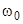 дается формулой (34), а
дается формулой (34), а 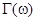 − выражением (35). Помещая химический потенциал в центр щели и заменяя в (37) нижний предел интегрирования на (
− выражением (35). Помещая химический потенциал в центр щели и заменяя в (37) нижний предел интегрирования на (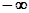 ), получим вклад в число заполнения от резонансного уровня
), получим вклад в число заполнения от резонансного уровня 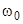 :
:
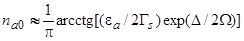 . (39)
. (39)
Считая аргумент арккотангенса большим по модулю, получим для 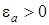
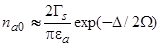 , (40)
, (40)
а для 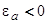
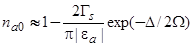 . (41)
. (41)
Сравним полученные значения 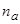 , с числами заполнения, отвечающими адсорбции атома с уровнем энергии
, с числами заполнения, отвечающими адсорбции атома с уровнем энергии 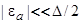 , но находящимся на поверхности не аморфной, а кристаллической подложки. Этот уровень
, но находящимся на поверхности не аморфной, а кристаллической подложки. Этот уровень 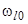 будет локальным. Число его заполнения
будет локальным. Число его заполнения 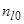 определяется по формуле
определяется по формуле
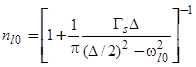 (42)
(42)
при условии, что уровень 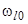 лежит ниже уровня химического потенциала. В противном случае
лежит ниже уровня химического потенциала. В противном случае 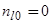 . Легко показать, что
. Легко показать, что
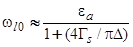 . (43)
. (43)
Сравнение 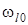 с энергией
с энергией 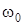 , определяемой выражением (36), дает
, определяемой выражением (36), дает
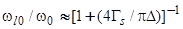 , (44)
, (44)
т. е. локальный уровень 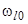 лежит ближе к центру щели, чем резонансный уровень
лежит ближе к центру щели, чем резонансный уровень 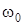 . Если и в кристаллическом полупроводнике положить
. Если и в кристаллическом полупроводнике положить 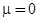 (середина запрещенной зоны), то из формулы (42) с учетом (43) получим для
(середина запрещенной зоны), то из формулы (42) с учетом (43) получим для 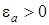 значение
значение 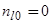 , а для
, а для 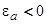
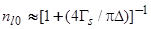 . (45)
. (45)
Сравнение случаев адсорбции на аморфных и кристаллических подложках показывает, что 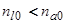 (выражение (41) с экспоненциальной точностью переходит в
(выражение (41) с экспоненциальной точностью переходит в 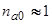 ).
).
Теперь рассмотрим случай 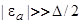 . При этом корень, отвечающий уравнению (27), также лежит в области энергий
. При этом корень, отвечающий уравнению (27), также лежит в области энергий 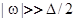 . Так как
. Так как 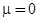 , представляет интерес только случай
, представляет интерес только случай 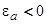 . Будем также считать, что
. Будем также считать, что 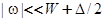 . Тогда
. Тогда
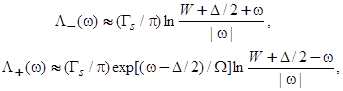 (46)
(46)
так что 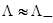 . Сделав естественное предположение, что
. Сделав естественное предположение, что 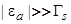 , получим
, получим 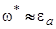 . Так как
. Так как
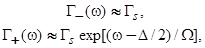 (47)
(47)
то
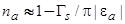 . (48)
. (48)
Для кристаллической подложки в том же приближении получим 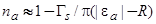 . Считая
. Считая 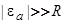 , получим
, получим 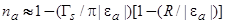 . Вновь приходим к выводу, что число заполнения адатома для адсорбции на аморфных подложках больше, чем при адсорбции на подложках кристаллических.
. Вновь приходим к выводу, что число заполнения адатома для адсорбции на аморфных подложках больше, чем при адсорбции на подложках кристаллических.
3.3. Конечные покрытия
До сих пор рассматривалась адсорбция одиночного атома. Энергия квазиуровня 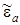 при наличии диполь-дипольного взаимодействия атомов в упорядоченном адсорбированном слое имеет вид
при наличии диполь-дипольного взаимодействия атомов в упорядоченном адсорбированном слое имеет вид 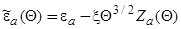 , где константа дипольного взаимодействия
, где константа дипольного взаимодействия 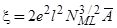 ,
, 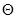 − относительная концентрация адатомов (степень покрытия, или отношение имеющихся адатомов к адсорбционным центрам) [1]. Вообще говоря, в случае полупроводниковой подложки здесь нужно учитывать диэлектрический фактор вида
− относительная концентрация адатомов (степень покрытия, или отношение имеющихся адатомов к адсорбционным центрам) [1]. Вообще говоря, в случае полупроводниковой подложки здесь нужно учитывать диэлектрический фактор вида 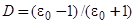 , где
, где 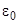 − статическая диэлектрическая проницаемость. Так как в типичных полупроводниках
− статическая диэлектрическая проницаемость. Так как в типичных полупроводниках 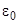 ~ 10, то D ~ 1. Поэтому диэлектрическую поправку можно опустить.
~ 10, то D ~ 1. Поэтому диэлектрическую поправку можно опустить.
Отметим еще одно упрощение реальной ситуации. При изменении покрытия от нулевого до монослойного, адатомы до некоторого значения 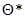 будут занимать эквивалентные позиции (например, позиции 1), но при превышении
будут занимать эквивалентные позиции (например, позиции 1), но при превышении 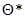 начинается заполнение позиции 2 (возможны и дальнейшие переходы. в позиции 3, 4 и т. д.). Такая ситуация, вообще говоря, должна соответствовать изломам на кривых изменения работы выхода с покрытием
начинается заполнение позиции 2 (возможны и дальнейшие переходы. в позиции 3, 4 и т. д.). Такая ситуация, вообще говоря, должна соответствовать изломам на кривых изменения работы выхода с покрытием 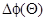 , что, как правило, в экспериментах не фиксируется. Поэтому и в случае кристаллической подложки под зарядом
, что, как правило, в экспериментах не фиксируется. Поэтому и в случае кристаллической подложки под зарядом 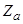 понимается некое среднее значение.
понимается некое среднее значение.
Как известно, субмонослойное покрытие, адсорбированное на кристаллической подложке, может быть как упорядоченным, так и неупорядоченным. Обычно в теории при этом рассматривают две модели энергетического рельефа поверхности: поверхность с глубокими потенциальными ямами и гладкая поверхность. В первом случае адатомы занимают поверхностные потенциальные ямы. Если энергия взаимодействия адатомов много меньше глубины такой ямы, адатомы располагаются случайным образом как в неупорядоченном сплаве. При 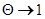 все поверхностные потенциальные ямы заполняются, и геометрия поверхностного слоя определяется геометрией грани подложки. При этом также важно, чтобы диаметр адсорбированной частицы
все поверхностные потенциальные ямы заполняются, и геометрия поверхностного слоя определяется геометрией грани подложки. При этом также важно, чтобы диаметр адсорбированной частицы 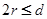 , где d — расстояние между ближайшими поверхностными атомами подложки. Если энергия взаимодействия адатомов превосходит глубину поверхностных ям и/или
, где d — расстояние между ближайшими поверхностными атомами подложки. Если энергия взаимодействия адатомов превосходит глубину поверхностных ям и/или 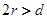 , говорят о гладкой поверхности. При этом также возможно образование как упорядоченных (в том числе, и несоизмеримых с подложкой), так и неупорядоченных структур, что зависит от характера взаимодействия адатомов. При адсорбции на аморфной подложке тоже могут образовываться и упорядоченные, и аморфные адсорбированные субмонослои. Если работает модель глубоких потенциальных ям, то пленка будет аморфной. Если же поверхность можно считать гладкой, то, в зависимости от характера взаимодействия между адатомами, могут образовываться как аморфные, так и упорядоченные слои.
, говорят о гладкой поверхности. При этом также возможно образование как упорядоченных (в том числе, и несоизмеримых с подложкой), так и неупорядоченных структур, что зависит от характера взаимодействия адатомов. При адсорбции на аморфной подложке тоже могут образовываться и упорядоченные, и аморфные адсорбированные субмонослои. Если работает модель глубоких потенциальных ям, то пленка будет аморфной. Если же поверхность можно считать гладкой, то, в зависимости от характера взаимодействия между адатомами, могут образовываться как аморфные, так и упорядоченные слои.
Расчеты показали, что значение коэффициента 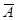 , входящего в выражение для константы диполь-дипольного взаимодействия, слабо зависит от геометрии адсорбированного слоя. Так, например, для квадратной решетки
, входящего в выражение для константы диполь-дипольного взаимодействия, слабо зависит от геометрии адсорбированного слоя. Так, например, для квадратной решетки 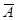 = 9.033, а для гексагональной −
= 9.033, а для гексагональной − 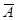 = 11.034. Ясно поэтому, что формулы (21) — (23) могут быть применены и для аморфных слоев, для которых, как и для регулярных структур, можно положить
= 11.034. Ясно поэтому, что формулы (21) — (23) могут быть применены и для аморфных слоев, для которых, как и для регулярных структур, можно положить 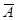 ~ 10 и рассматривать
~ 10 и рассматривать 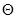 как среднюю степень покрытия, определяемую двумерной плотностью пленки. Такая ситуация объясняется тем обстоятельством, что взаимодействие перпендикулярных к поверхности диполей, образованных заряженными адатомом и его изображением в подложке, обладает цилиндрической симметрией и зависит только от радиуса
как среднюю степень покрытия, определяемую двумерной плотностью пленки. Такая ситуация объясняется тем обстоятельством, что взаимодействие перпендикулярных к поверхности диполей, образованных заряженными адатомом и его изображением в подложке, обладает цилиндрической симметрией и зависит только от радиуса 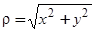 (z = 0 — координата поверхности).
(z = 0 — координата поверхности).
Есть еще один момент, который следует обсудить. Формулы (21) и (23) предполагают, что все адатомы на поверхности идентичны, т. е. обладают одинаковым зарядом 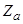 . Что касается адсорбции на монокристаллической поверхности, то для выполнения этого условия достаточно предположить, что все адатомы находятся в эквивалентных кристаллографических позициях. В случае же адсорбции на аморфной подложке под
. Что касается адсорбции на монокристаллической поверхности, то для выполнения этого условия достаточно предположить, что все адатомы находятся в эквивалентных кристаллографических позициях. В случае же адсорбции на аморфной подложке под 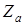 следует понимать усредненное по всему адсорбированному слою значение зарядов адатомов.
следует понимать усредненное по всему адсорбированному слою значение зарядов адатомов.
Таким образом, заметное различие чисел заполнения адатома для моделей аморфной и кристаллической подложек проявляется только в том случае, когда уровень адатома 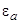 перекрывается с областью
перекрывается с областью 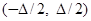 , отвечающей запрещенной зоне (кристаллический полупроводник) или щели подвижности (аморфный полупроводник). При этом число заполнения адатома в аморфном случае больше, чем в кристаллическом. Соответственно, заряд
, отвечающей запрещенной зоне (кристаллический полупроводник) или щели подвижности (аморфный полупроводник). При этом число заполнения адатома в аморфном случае больше, чем в кристаллическом. Соответственно, заряд 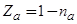 атома, адсорбированного на аморфной подложке, меньше, чем у атома, адсорбированного на подложке кристаллической.
атома, адсорбированного на аморфной подложке, меньше, чем у атома, адсорбированного на подложке кристаллической.
4. Адсорбция на поликристаллических подложках
С точки зрения адсорбции и электронной эмиссии (как термоэлектронной, так и полевой), поликристаллическая подложка представляет собой поверхность, содержащую набор различных граней i, каждой из которых соответствует свои площадь 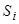 и работа выхода
и работа выхода 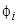 . Иногда в связи с этим говорят о пятнистой поверхности. Встает вопрос: при каких условиях допустимо ввести для каждого i-го пятна свое значение
. Иногда в связи с этим говорят о пятнистой поверхности. Встает вопрос: при каких условиях допустимо ввести для каждого i-го пятна свое значение 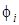 ? Воспользуемся результатами работы [17], где показано, что если электрон рассматривать как волновой пакет, то неопределенность его кинетической энергии при движении в направлении х, параллельном поверхности (x, y, 0), равна
? Воспользуемся результатами работы [17], где показано, что если электрон рассматривать как волновой пакет, то неопределенность его кинетической энергии при движении в направлении х, параллельном поверхности (x, y, 0), равна
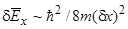 , (49)
, (49)
где 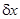 − среднее квадратичное отклонение координаты. Если считать, что
− среднее квадратичное отклонение координаты. Если считать, что 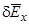 есть величина порядка
есть величина порядка 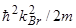 , где
, где 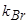 — значение волнового вектора на границе зоны Бриллюэна, равное, по порядку величины,
— значение волнового вектора на границе зоны Бриллюэна, равное, по порядку величины, 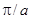 (а — постоянная решетки для данной грани), то
(а — постоянная решетки для данной грани), то
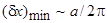 . (50)
. (50)
Таким образом, 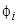 можно считать хорошей локальной характеристикой неоднородной поверхности.
можно считать хорошей локальной характеристикой неоднородной поверхности.
Рассмотрим адсорбцию одиночного атома на i-ом пятне [18]. Число заполнения 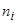 такого атома согласно модели Фндерсона [1,2] может быть записано в виде
такого атома согласно модели Фндерсона [1,2] может быть записано в виде
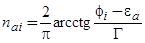 , (51)
, (51)
где энергия квазиуровня адатома 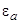 отсчитывается от вакуума. Здесь мы исключаем зависимость положения квазиуровня
отсчитывается от вакуума. Здесь мы исключаем зависимость положения квазиуровня 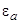 и его полуширины
и его полуширины 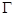 от конкретной i-ой грани. Такая зависимость может, в принципе, возникать из-за различий геометрии граней и соответствующих электронных плотностей.
от конкретной i-ой грани. Такая зависимость может, в принципе, возникать из-за различий геометрии граней и соответствующих электронных плотностей.
Введем степень покрытия i-ой грани адатомами, определив ее как
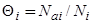 , (52)
, (52)
где 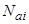 − плотность адсорбированных на i-ой грани атомов,
− плотность адсорбированных на i-ой грани атомов, 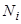 − плотность адсорбционных центров на i-ой грани. Тогда с учетом диполь-дипольного отталкивания для заряда
− плотность адсорбционных центров на i-ой грани. Тогда с учетом диполь-дипольного отталкивания для заряда 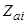 атома, адсорбированного на i-ом пятне, и изменения работы выхода
атома, адсорбированного на i-ом пятне, и изменения работы выхода 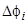 , вызванного адсорбцией, получим следующие выражения:
, вызванного адсорбцией, получим следующие выражения:
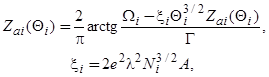 (53)
(53)
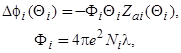 (54)
(54)
где 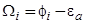 , x — константа диполь — дипольного отталкивания адатомов, 2l-плечо поверхностного диполя, А~10 (по поводу изменения работы выхода см. подробнее [1]). Вводя относительную площадь
, x — константа диполь — дипольного отталкивания адатомов, 2l-плечо поверхностного диполя, А~10 (по поводу изменения работы выхода см. подробнее [1]). Вводя относительную площадь 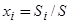 , занимаемую i-ым пятном на поверхности с площадью
, занимаемую i-ым пятном на поверхности с площадью 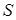 , получим интегральное снижение работы выхода
, получим интегральное снижение работы выхода 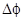 в виде
в виде
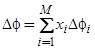 , (55)
, (55)
где 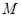 — число пятен на поверхности, причем по определению
— число пятен на поверхности, причем по определению
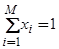 , (56)
, (56)
Определим теперь значение изменение работы выхода усредненного пятна 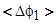 , так, чтобы имело место тождество
, так, чтобы имело место тождество
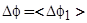 , (57)
, (57)
где
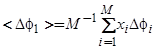 . (58)
. (58)
С другой стороны, из (54) следует, что
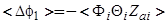 . (59)
. (59)
Введем теперь полное число адсорбционных центров на поверхности, которое, как не трудно догадаться, равно числу адатомов в монослое 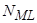 :
:
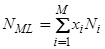 . (60)
. (60)
Полное число занятых адатомами узлов 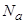 равно
равно
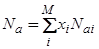 , (61)
, (61)
причем степень заполнения всей поверхности 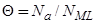 . Таким образом, вводя энергию
. Таким образом, вводя энергию 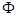 и заряд адатомов
и заряд адатомов 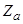 , характеризующие данную поверхность в целом, имеем соотношение
, характеризующие данную поверхность в целом, имеем соотношение
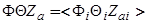 . (62)
. (62)
Будем считать, что адсорбированные атомы распределяются по поверхности случайным образом. Это будет иметь место при низких температурах, когда барьеры для поверхностной диффузии значительно выше 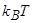 , и адатом постоянно находится на том же центре, куда попал при осаждении. Тогда
, и адатом постоянно находится на том же центре, куда попал при осаждении. Тогда
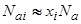 . (63)
. (63)
Поделив обе части равенства (63) на 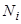 и учитывая (60) получим
и учитывая (60) получим
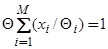 . (64)
. (64)
Положив в этом выражении 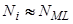 и
и 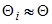 , что в дополнение к предположению о случайном характере заполнения поверхности адатомами включает и гипотезу о приблизительно одинаковой плотности адсорбционных центров в различных пятнах (т. е. игнорирование различия геометрии граней), получим тождество (56) и
, что в дополнение к предположению о случайном характере заполнения поверхности адатомами включает и гипотезу о приблизительно одинаковой плотности адсорбционных центров в различных пятнах (т. е. игнорирование различия геометрии граней), получим тождество (56) и 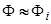 . Теперь имеем
. Теперь имеем
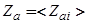 , (65)
, (65)
где теперь
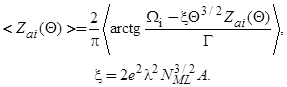 (66)
(66)
Здесь случайной величиной является энергия 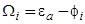 . Предположим, что распределение значений
. Предположим, что распределение значений 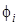 подчиняется закону равнораспределения с плотностью вероятности
подчиняется закону равнораспределения с плотностью вероятности
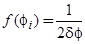 при
при 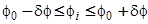 ,
,
= 0 в остальных случаях. (67)
Тогда
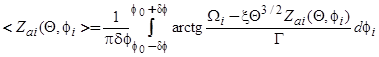 . (68)
. (68)
Рассмотрим сперва нулевые покрытия, т. е. адсорбцию одиночного адатома, заряд которого обозначим как 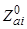 . Здесь речь идет об адатоме, попадающим на i-е пятно. Тогда
. Здесь речь идет об адатоме, попадающим на i-е пятно. Тогда
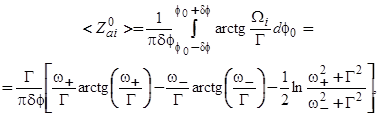 (69)
(69)
где 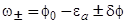 .
.
Из формулы (69) следует, что при 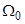 = 0 усредненный заряд изолированного адатома
= 0 усредненный заряд изолированного адатома 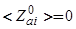 . Объясняется этот результат просто: при
. Объясняется этот результат просто: при 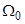 =0 центр тяжести квазиуровеня адатома совпадает с уровнем Ферми субстрата, в результате чего какого-либо обмена электронами между адатомом и подложкой не происходит. Если
=0 центр тяжести квазиуровеня адатома совпадает с уровнем Ферми субстрата, в результате чего какого-либо обмена электронами между адатомом и подложкой не происходит. Если 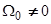 и удовлетворяет неравенству
и удовлетворяет неравенству 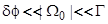 , то с точностью до
, то с точностью до 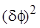 получим
получим 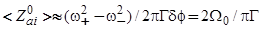 . Этот результат не зависит от поликристалличности, т. е. заряд адатома такой же, как и на монокристаллической подложке. Если же
. Этот результат не зависит от поликристалличности, т. е. заряд адатома такой же, как и на монокристаллической подложке. Если же 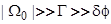 , то
, то
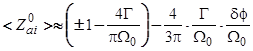 , (70)
, (70)
где знаки 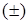 относятся к случаям
относятся к случаям 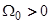 и
и 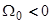 соответственно. Здесь первая неисчезающая поправка по
соответственно. Здесь первая неисчезающая поправка по 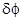 имеет на самом деле второй порядок малости. Таким образом, в пределах
имеет на самом деле второй порядок малости. Таким образом, в пределах 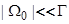 и
и 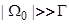 поправки малы. Из выражения (70) также следует, что в случае положительного заряда адатома поликристалличность этот заряд понижает, тогда как при отрицательном заряде адатома поликристалличность увеличивает значение его модуля. Этот результат совпадает с влиянием аморфизации поверхности на зарядовое состояние адатомов (см. п.2).
поправки малы. Из выражения (70) также следует, что в случае положительного заряда адатома поликристалличность этот заряд понижает, тогда как при отрицательном заряде адатома поликристалличность увеличивает значение его модуля. Этот результат совпадает с влиянием аморфизации поверхности на зарядовое состояние адатомов (см. п.2).
Мы здесь не приводим подробный, изобилующий громоздкими формулами анализ выражения (74), отсылая заинтересованного читателя к работе [18]. Анализ показывает, что поликристалличность подложки максимальным образом сказывается при малых покрытиях, причем для адатомов, величина заряда которых 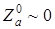 , что, как известно, характеризует адсорбцию газов на металлах и полупроводников.
, что, как известно, характеризует адсорбцию газов на металлах и полупроводников.
Литература:
1. Давыдов С. Ю., Лебедев А. А., Посредник О. В. Физика поверхности и границ раздела.: Учеб. пособие, СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2005, 66 с.
2. Давыдов С. Ю., Лебедев А. А., Посредник О. В. Введение в физику наносистем.: Учеб. пособие, СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2009, 112 с.
3. Anderson P. W. Localized magnetic states in metals // Phys. Rev. 1961.V. 124. N. 1. P. 41–53.
4. Newns D. M. Self-consistent model of hydrogen chemisorption // Phys. Rev. 1969. V.178. N. 3. P. 1123–1135.
5. Давыдов С. Ю., Трошин С. В. Адсорбция на металлах и полупроводниках: модели Андерсона-Ньюнса и Халдейна-Андерсона // ФТТ. 2007. Т.49, В. 8. С. 1508–1513.
6. Давыдов С. Ю., Павлык А. В. Адсорбция редкоземельных металлов на кремнии: изменение работы выхода // ФТТ. 2003. Т. 45. В.7. С. 1325–1328.
7. Давыдов С. Ю., Павлык А. В. Адсорбция ванадия на рутиле // Письма в ЖТФ. 2003. Т. 29. В. 12. С. 33–36.
8. Давыдов С. Ю., Павлык А. В. Адсорбция щелочных металлов на поверхности (100) кремния: изменение работы выхода // ЖТФ. 2004. Т. 74. В. 8. С. 95–99.
9. Давыдов С. Ю., Мошников В. А., Федотов А. А. Адсорбция газов на полупроводниковых оксидах: изменение работы выхода // Письма в ЖТФ. 2004. Т. 30. В. 17. С. 39–44.
10. Давыдов С. Ю. Простые модели адсорбции водорода на германии // ЖТФ. 2005. Т. 75. В.1. С.112–114.
11. Давыдов С. Ю. Адсорбция атомов водорода на кремнии // ЖТФ. 2005. Т. 75. Вып. 1. С.141–142.
12. Давыдов С. Ю., Мошников В. А., Федотов А. А. Адсорбция молекул кислорода и окиси углерода на диоксиде титана // ЖТФ. 2006. Т. 76. Вып. 1. С. 141–142.
13. Haldane F. D. M., Anderson P. W. Simple model of multiple charge states of transition-metal impurities in semiconductors // Phys. Rev. B. 1976. V. 13. N. 6. P. 2553–2559.
14. Губанов А. И. Квантово-электронная теория аморфных проводников (М.-Л., изд-во АН СССР, 1963), 250 с.
15. Шкловский Б. И., Эфрос А. Л. Электронные свойства легированных полупроводников (М., Наука, 1979), 416 с.
16. Займан Дж. Модели беспорядка (М., Мир, 1982), 592 с.
17. Давыдов С. Ю. О локальной работе выхода // ЖТФ. 1979. Т. 49. В. 1. С. 211–212.
18. Давыдов С. Ю., Трошин С. В. Об адсорбции на поликристаллических положках //ЖТФ. 2008. Т. 78. В. 5. С. 134–137.







