Изложена математическая модель формирования длительности цикля для лесопильных станков. Приведены регрессионные уравнения зависимостей величин формирующих длительность цикла от доминирующих факторов.
Основой математической модели формирования длительностей цикла tД для станочного оборудования является математическое описание случайной величины tД.
Длительность цикла деления лесоматериалов tД на станках в цехах, как случайная величина, описывается различными функциями. По исследованиям кафедры ТОЛП УГЛТУ в большинстве случаев это логарифмически нормальное распределение (52,1 % выборок). С нормальным распределением согласуются 31,8 % выборок. В остальных случаях (16,1 %) величина tД не противоречит распределениям Эрланга и экспоненциальному. У 24 выборок из 189 сходимость по критерию Р(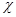 2) оказалось несколько меньше критического значения 0,1 [1].
2) оказалось несколько меньше критического значения 0,1 [1].
Среди факторов, обуславливающий случайный характер tД, существуют доминирующие. Это параметры лесоматериалов и их деления. Учет их влияния на величину tД возможен различными способами.
Изучение схем деления лесоматериалов показало, что основным обобщающим параметром, характеризующим деление и влияющим на величину tД, является постав или что тоже самое — число резов np, зависящее как от размерно-качественных параметров лесоматериалов, так и от размеров готовой продукции. Приняв это во внимание и на основании теории производительности машин и механизмов, величина tД для цикло-проходных станков и однопозиционных торцовочных запишется в виде
tД = np t1p,
а для проходных станков при продольном делении лесоматериалов
tД = tM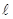 +tП,
+tП,
где t1p — цикловое время на один рез; tM — длительность деления единицы длины лесоматериала, зависящая от постава; 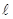 — длина лесоматериала; tП — длительность циклового простоя.
— длина лесоматериала; tП — длительность циклового простоя.
Длительность цикла tД для станков Гр-деления круглых лесоматериалов представляют в виде двух слагаемых — длительности деления бревна tl и tП. Первое слагаемое определяется произведением сомножителей tМ и 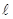 , а длительность циклового простоя tП, согласно теории производительности (на примере лесопильной рамы)
, а длительность циклового простоя tП, согласно теории производительности (на примере лесопильной рамы)
tП = tВ — tC,
где tB — время выполнения вспомогательных операций.
Длительность деления свободного конца бревна tC составляет
tC = tM 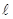 C,
C,
где lC — длина свободного конца бревна.
Величина tB, как известно, состоит из следующей суммы затрат на выполнение элементов цикла
tB = tX + tЗ + tP + tЗЛ,
где tX — время на разжим бревна и холостой ход тележки; tЗ — время загрузки тележки бревном, зажима его и ориентирования по порокам; tP — время рабочего хода; tЗЛ — время загрузки лесопильной рамы бревном и надвигания его до пил.
Перечисленные составляющие цикла tД являются случайными величинами. Приведённое ниже статистическое описание длительностей выполнения элементов цикла получено для коротышёвой рамы РК по статистическим замерам 1608 брёвен, собранным в производственных условиях Камышловского цеха в летний период. Постав за весь период наблюдений был равен 32–60–60–60–32. Околостаночные операции не механизированы. Сбор статистических данных производился по методике [2, 3], обработка по методике [4], проверка на адекватность приведена в работе [5].
Результаты статистической обработки распределений случайных величин tЗ, tР, tМ, tХ, lС для указанных условий позволили получить регрессионные уравнения зависимостей параметров случайных величин tЗ, tМ (для берёзы и осины) и lС от доминирующего фактора (табл. 1). Распространение полученных статистических данных для других моделей лесопильных рам и других условий их функционирования, отличающихся от условий в Камышловском цехе, возможно введением поправочных коэффициентов. Учитывая это, для дальнейших исследований принимаются следующие математические модели параметров функционирования лесопильной рамы.
Длительность загрузки тележки бревном подчиняется нормальному закону с параметрами 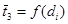 и
и 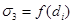 , уравнения которых указаны в таблице 1.
, уравнения которых указаны в таблице 1.
Таблица 1
Регрессионные уравнения зависимостей величин tЗ, tР, tМ, tХ, lС от доминирующих факторов
|
Уравнение |
|
|
|
|
Коэффициенты уравнений определены при |
№ ур-я |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
- |
- |
19,82 |
1,69 |
11,5 см≤di≤37,5 см |
(1) |
|
|
- |
- |
25,85 |
1,69 |
(2) |
|
|
|
- |
- |
- |
- |
- |
(3) |
|
|
- |
- |
- |
- |
- |
(4) |
|
|
0,99 |
0,005 |
50,16 |
1,75 |
190 мм≤h≤1770 мм |
(5) |
|
|
- |
- |
3,54 |
1,75 |
(6) |
|
|
|
0,98 |
0,007 |
42,49 |
2,04 |
200 мм≤h≤2130 мм |
(7) |
|
|
- |
- |
17,03 |
2,04 |
(8) |
|
|
|
- |
- |
- |
- |
- |
(9) |
|
|
- |
- |
- |
- |
- |
(10) |
|
|
- |
- |
53,65 |
2,37 |
100 см≤li≤305 см |
(11) |
|
|
- |
- |
4,98 |
2,60 |
160 см≤li≤305 см |
(12) |
Примечания: ±r и mr — коэффициент корреляции и его ошибка; FФ и F0,05 — критерии Фишера (фактическое значение и при F=0,05).
Длительность рабочего хода немеханизированной тележки описывается логарифмически нормальным законом. При перемещении её на расстояние SН=3 м среднее значение 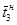 =6,36 с среднеквадратическое отклонение
=6,36 с среднеквадратическое отклонение 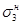 =1,36 с (при обработке статистических данных о затратах времени tР использовались только те замеры, в которых брёвна подавались в лесопильную раму без ожидания распиловки). Учитывая, что значения SН в других производственных условиях могут быть другими, можно записать:
=1,36 с (при обработке статистических данных о затратах времени tР использовались только те замеры, в которых брёвна подавались в лесопильную раму без ожидания распиловки). Учитывая, что значения SН в других производственных условиях могут быть другими, можно записать:
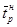 =6,36 SН/3, с;
=6,36 SН/3, с; 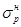 =0,214
=0,214 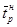 , с.
, с.
Для механизированных тележек и конвейеров принимаем
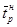 = SН/VР;
= SН/VР; 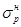 =0,
=0,
где VР — скорость перемещения бревна впереди рамным устройством (по паспортной характеристике), м/с.
Длительность холостого хода не противоречит логнормальному закону. Статистики величины tХ следующие
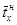 =9,04SН/3, с;
=9,04SН/3, с; 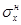 =0,352
=0,352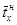 , с;
, с;
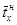 =SН/VХ, с;
=SН/VХ, с; 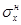 =0.
=0.
Продолжительность загрузки бревна толщиной di в лесопильную раму 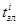 состоит из двух слагаемых
состоит из двух слагаемых
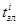 =
=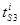 +
+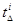 ,
,
где 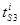 — затраты времени на подачу i-го бревна в передние приводные вальцы;
— затраты времени на подачу i-го бревна в передние приводные вальцы; 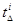 — время надвигания i-го бревна до пил со скоростью i — 1 бревна
— время надвигания i-го бревна до пил со скоростью i — 1 бревна 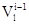 на расстояние
на расстояние 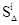 .
.
Первое слагаемое 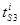 в математической модели определяется
в математической модели определяется
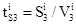 .
.
Здесь 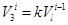 , где к — коэффициент, учитывающий трение бревна о передние приводные вальцы, при подаче его в них, 0,5;
, где к — коэффициент, учитывающий трение бревна о передние приводные вальцы, при подаче его в них, 0,5; 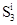 — расстояние подачи i-го бревна от передних приводных вальцов.
— расстояние подачи i-го бревна от передних приводных вальцов.
Параметр 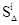 — путь, который i-ое бревно пройдёт со скоростью i-1 бревна, равен
— путь, который i-ое бревно пройдёт со скоростью i-1 бревна, равен
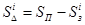 ,
,
где SП — расстояние от передних приводных вальцов до пильных полотен.
Расстояние подачи 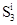 в модели зависит от состояния смежных торцов брёвен (рис. 1). В идеальном случае, встреча торцов брёвен происходит перед передними вальцами (рис. 1а). Следующие основные состояния рассматриваются в момент конца рабочего хода тележки с i-ым бревном
в модели зависит от состояния смежных торцов брёвен (рис. 1). В идеальном случае, встреча торцов брёвен происходит перед передними вальцами (рис. 1а). Следующие основные состояния рассматриваются в момент конца рабочего хода тележки с i-ым бревном 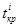 и начала подачи его в передние вальцы
и начала подачи его в передние вальцы 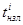 .
.
Во втором случае, в момент времени 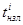 , задний торец i-1 бревна находится между пильными полотнами и передними вальцами (рис. 1б, 1в). В третьем случае, в тот же момент времени — за пильными полотнами (рис. 1г, 1д).
, задний торец i-1 бревна находится между пильными полотнами и передними вальцами (рис. 1б, 1в). В третьем случае, в тот же момент времени — за пильными полотнами (рис. 1г, 1д).
При прохождении брёвен через лесопильную раму без межторцовых разрывов (рис. 1а) текущее время прохождения заднего торца i-1 бревна через передние вальцы 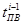 равно текущему времени
равно текущему времени 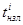 . В этой ситуации текущее время начала деления i-го бревна совпадает с текущим временем конца деления i-1 бревна, т. е.
. В этой ситуации текущее время начала деления i-го бревна совпадает с текущим временем конца деления i-1 бревна, т. е. 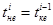 и, следовательно, затраты времени
и, следовательно, затраты времени 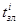 полностью совмещаются с временем деления свободного конца i-1 бревна
полностью совмещаются с временем деления свободного конца i-1 бревна 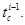 Значение
Значение 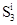 для рассмотренного состояния смежных торцов брёвен принято равным
для рассмотренного состояния смежных торцов брёвен принято равным 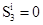 .
.
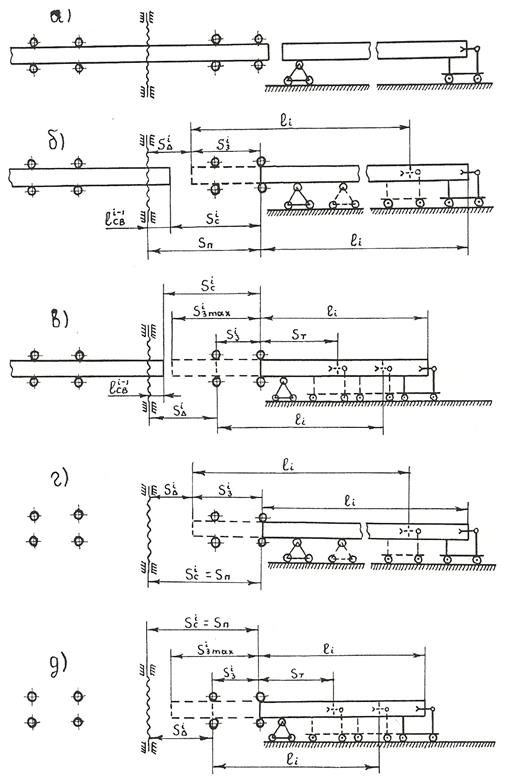
Рис. 1. Состояние смежных торцов брёвен при загрузке лесопильной рамы
Во втором случае, при 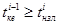 , возможны два варианта, зависящие от длины i-го бревна li и параметров
, возможны два варианта, зависящие от длины i-го бревна li и параметров 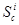 ,
, 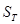 , где
, где 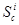 — межторцовой разрыв в момент времени
— межторцовой разрыв в момент времени 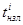 ;
; 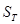 — минимальное расстояние от переднего вальца до клещей зажимной тележки. При
— минимальное расстояние от переднего вальца до клещей зажимной тележки. При 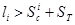 (рис. 1б), т. е. при достаточной длине бревна для возможного устранения межторцового разрыва
(рис. 1б), т. е. при достаточной длине бревна для возможного устранения межторцового разрыва 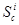 , определение
, определение 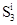 при принято по формуле
при принято по формуле
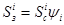 ,
,
где 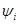 — случайное число генерируемое по равномерному закону в интервале [0, 1]. В противном случае, т. е. при
— случайное число генерируемое по равномерному закону в интервале [0, 1]. В противном случае, т. е. при 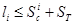 (рис. 1в). имеем
(рис. 1в). имеем
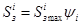 ,
,
где 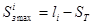 — максимально возможное устранение межторцового разрыва.
— максимально возможное устранение межторцового разрыва.
Значение 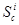 для случая, изображённого на рис. 1б
для случая, изображённого на рис. 1б
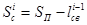 ,
,
где 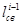 — длина свободного конца бревна в момент времени
— длина свободного конца бревна в момент времени 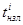 .
.
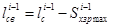 ,
,
где 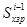 — путь пройденный i-1 бревном за время выполнения вспомогательных операций с i-ым бревном
— путь пройденный i-1 бревном за время выполнения вспомогательных операций с i-ым бревном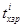 .
.
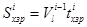 ,
,
где 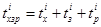 .
.
В третьем случае, когда 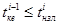 (рис. 1г, 1д), предусмотрены также два варианта, аналогично рассмотренным ранее. Если
(рис. 1г, 1д), предусмотрены также два варианта, аналогично рассмотренным ранее. Если 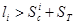 (рис. 1г)
(рис. 1г) 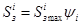 , а
, а 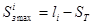 . При
. При 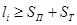 (рис. 1д)
(рис. 1д) 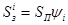 .
.
Величину подачи для лесопильных рам устанавливают исходя из работоспособности пил, качества пиления и мощности рамы по источнику [6] подача на один оборот рамы при распиловке хвойной древесины для моделей РД 50–3, РД 75–7 и РД 80–2 изменяется обратно пропорционально суммарной высоте запила 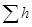 по гиперболической кривой от 52 мм до 8 мм. При малых значениях
по гиперболической кривой от 52 мм до 8 мм. При малых значениях 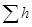 расчётные подачи велики, но их ограничивают по условиям качества пиления до 44 мм.
расчётные подачи велики, но их ограничивают по условиям качества пиления до 44 мм.
Для малого лесопиления на одноэтажных рамах имеются сведения в источнике [7].
Длительности деления единицы длины бревна (1м) tМ для брёвен по толщине из мелкой и средней групп лесоматериалов не противоречат логнорманому распределению, а из крупной — нормальному. Средние значения 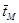 и СКО
и СКО 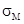 для берёзы и осины зависят от di. Для учёта поставов лесопильных рам вместо толщин брёвен di введены суммарные высоты пропилов
для берёзы и осины зависят от di. Для учёта поставов лесопильных рам вместо толщин брёвен di введены суммарные высоты пропилов 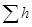 , приходящихся на одно бревно. В этой связи, среднее значение продолжительности деления брёвен
, приходящихся на одно бревно. В этой связи, среднее значение продолжительности деления брёвен 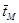 толщиной di. на лесопильной раме модели М с ходом пильной рамы Н, частотой вращения главного вала n принимается равным
толщиной di. на лесопильной раме модели М с ходом пильной рамы Н, частотой вращения главного вала n принимается равным
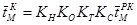 ,
,
а СКО (по коэффициенту вариаций случайной величины 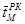 )
)
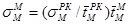 .
.
Здесь 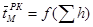 и
и 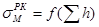 — статистики случайной величины для коротышёвой рамы РК, определяемые для берёзы и осины по формулам табл. 1; KH =410/H — коэффициент, учитывающий ход пильной рамки; КО=215/n — коэффициент, учитывающий частоту вращения коленвала лесопильной рамы; КТ — коэффициент, учитывающий сезон работы рамы (для летних условий КТ=1, для зимних КТ=1,1); КС — коэффициент, учитывающий сортность брёвен (для 1…2 с. КС=0,78…0,85; для 3 с. КС=1) [8].
— статистики случайной величины для коротышёвой рамы РК, определяемые для берёзы и осины по формулам табл. 1; KH =410/H — коэффициент, учитывающий ход пильной рамки; КО=215/n — коэффициент, учитывающий частоту вращения коленвала лесопильной рамы; КТ — коэффициент, учитывающий сезон работы рамы (для летних условий КТ=1, для зимних КТ=1,1); КС — коэффициент, учитывающий сортность брёвен (для 1…2 с. КС=0,78…0,85; для 3 с. КС=1) [8].
Определение среднего значения раскроя сосновых брёвен длиной 1 м 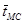 возможен по формуле, выведенной для дальнейшего использования
возможен по формуле, выведенной для дальнейшего использования
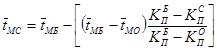 ,
,
где КП — коэффициент, учитывающий изменение удельного сопротивления резанию в зависимости от породы (для берёзы — 1,25, сосны — 1, осины — 0,85).
Вывод зависимости 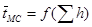 возможен при определении координат точек М
возможен при определении координат точек М 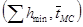 , N
, N 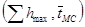 , составлении и решении двух линейных уравнений с двумя неизвестными
, составлении и решении двух линейных уравнений с двумя неизвестными
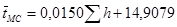 , с.
, с.
Длина свободного конца бревна lс, необходимая для определения параметра tc, как случайная величина, зависит от группы распиливаемого сырья по длине. Распределения lс не противоречат нормальному закону, параметры которого 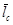 и
и 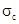 определяются через доминирующий фактор — длину брёвен по формулам табл. 1.
определяются через доминирующий фактор — длину брёвен по формулам табл. 1.
Полученные модели положены в основу моделирующего алгоритма по формированию параметров распиловки.
Литература:
1. Лившиц Н. В., Обвинцев В. В., Чамеев В. В. Математическое описание операций раскроя сырья и полуфабрикатов в лесоперерабатывающих цехах леспромхозов // Межвуз. сб. науч. тр. / Ленингр. лесотех. акад.-1977. — Вып. 6. — Лесосечные, лесоскладские работы и сухопутный транспорт леса. — С. 106–110.
2. Еремеев А. А., Федотова О. А., Бобыкина Е. Г., Чамеев В. В. Статисти ческие наблюдения за функционированием лесотехнического объекта // Леса России и хозяйство в них: Вып. 1 (35) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2010.- С. 64- 68.
3. Еремеев А. А., Федотова О. А., Бобыкина Е. Г., Чамеев В. В., Меньшиков Б. Е. Разработка журнала статистических наблюдений для станков проходного типа при раскрое круглых лесоматериалов на пилопродукцию // Леса России и хозяйство в них: Вып. 2 (36) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2010.- С. 51–57.
4. Еремеев А. А., Федотова О. А., Бобыкина Е. Г., Сафонов А. А., Ивачёва К. В., Терентьев В. В., Чамеев В. В. Вероятностно-статистическая модель операции пиления круглых лесоматериалов для станков проходного типа // Леса России и хозяйство в них: Вып. 3 (37) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2010.- С. 53–63.
5. Еремеев А. А., Бобыкина Е. Г., Сафонов А. А., Ивачёва К. В., Терентьев В. В., Чамеев В. В. Проверка математических моделей, алгоритмов и программ комплекс-программы «ЦЕХ» на адекватность реальным производственным условиям лесообрабатывающих цехов по переработке круглых лесоматериалов на пилопродукцию // Научное творчество молодёжи — лесному комплексу России: матер. VII Всерос. научн.-техн. конф. / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2011. Ч.1.- С. 29–31.
6. Головач, А. Ф. Электрические машины и электромашин деревообрабатывающих станков / А. Ф. Головач. — М.: Лесная промышленность, 1968. — 338 с.
7. Оптимизация производственных процессов лесоперерабатывающих цехов леспромхозов по переработке низкокачественной древесины: Отчет о НИР/УЛТИ N 24/78–3; Руководитель Н. В. Лившиц; исполн.В. В. Обвинцев, В. В. Чамеев и др.; N ГР 80032639; Инв.N Б977002. — Свердловск, 1980–94 c.
8. Переработка низкокачественных бревен / В. Ф. Ветшева, В. А. Горн, В. Н. Хлебодаров, З. Т. Чанчикова. — М.: Лесная промышленность, 1982. — 80 с.







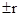
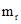
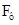
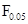
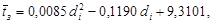 с
с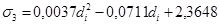 , с
, с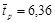 с
с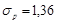 с
с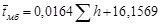 , с
, с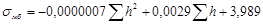 , с
, с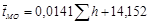 , с
, с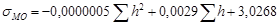
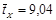 , с
, с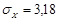 , с
, с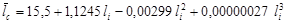 , см
, см , см
, см