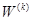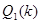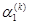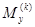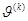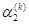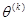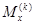На основе теории малых упруго-пластических деформаций сформулированы краевые задачи пространственных стержней при повторных и переменных нагружениях. Исследована сходимость реализованных алгоритм.
Ключевые слова: Система дифференциальных уравнений, метод Канторович — Власова, упруго-пластическая деформация, центральная конечная разность.
Marginal problems spatial pegs are worded on base of the theories small springy-plastic deformation under the repeated and variable load. Explored convergence marketed algorithm.
На основе теории малых упруго-пластических деформаций [1] и гипотезы, предложенной В. З. Власовым, Г. Ю. Джанелидзе и В. К. Кабуловым в данной работе исследуются напряженно-деформированные состояния стержней пространственным нагружённые с учетом пластических деформаций.
Система дифференциальных уравнений для пространственного стержня прямоугольного сечения при повторно-переменном упруго–пластическом нагружении описывается следующим образом [1,4]:
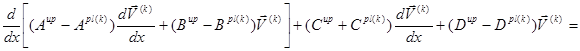
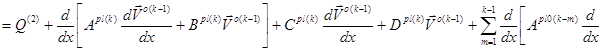
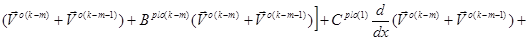
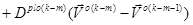 (1)
(1)
где
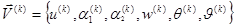 ,
, 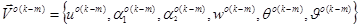
Здесь 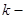 число нагружённый (
число нагружённый (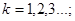
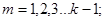 )
) 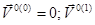 соответствует значением
соответствует значением 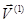 в точке
в точке 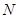 (Рис.1)
(Рис.1)
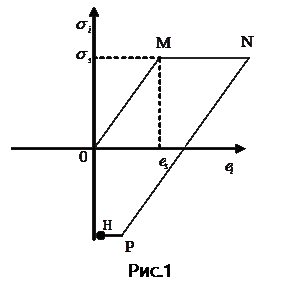
Коэффициенты векторного уравнения (1) определяются по следующим формулам. [1,2]:
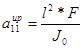 ,
, 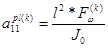 ,
, 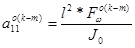 ,
,
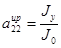 ,
, 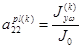 ,
, 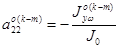 ,
,
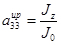 ,
, 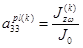 ,
, 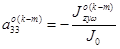 ,
,
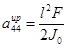 ,
, 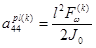 ,
, 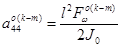 ,
,
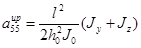 ,
, 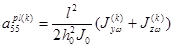 ,
, 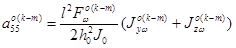 ,
,
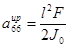 ,
, 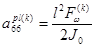 ,
, 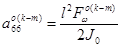
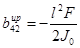 ,
, 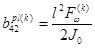 ,
, 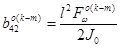
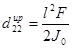 ,
, 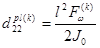 ,
, 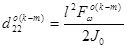
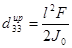 ,
, 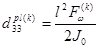 ,
, 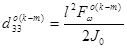
Здесь
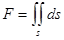 ,
, 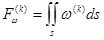 ,
, 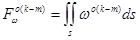
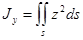
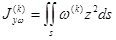
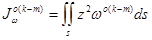
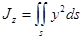
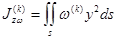
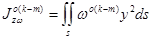
Подынтегральная функция 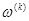 при
при 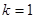 имеет вид [2,3,4]:
имеет вид [2,3,4]:
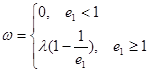
И при 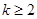
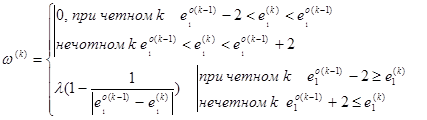
Здесь, 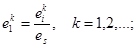 ,
, 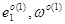 соответствуют значениям
соответствуют значениям 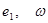 в точки
в точки 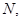 а
а 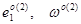 — значениям
— значениям 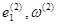 в точки
в точки 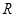 (Рис.1)
(Рис.1)
Приведенное векторное дифференциальное уравнение (1) решается при граничных условиях: (один конец стержня защемлен, а другой нагружен сосредоточенной массой):
При х=0
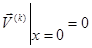 (2)
(2)
При 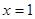

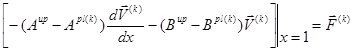 (3)
(3)
Где
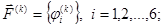
При четном 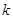
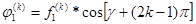 ,
,
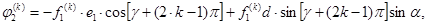
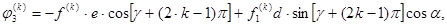
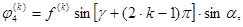
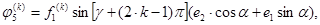
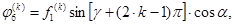
При нечетном
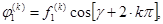
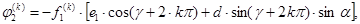
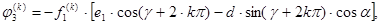
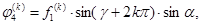
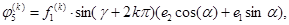
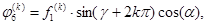
В векторном уравнении (1) внешние нагрузки имеют вид
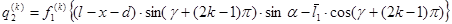
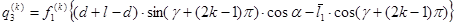
При нечетном 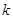 и
и
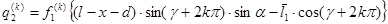
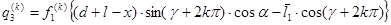
Пользуясь центральными конечно-разностными соотношениями, аппроксимирующими производные с точностью второго порядка в области 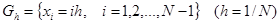 , из векторного уравнение (1) и граничных условий (2), (3) получим систему не линейных алгебраических уравнений [4];
, из векторного уравнение (1) и граничных условий (2), (3) получим систему не линейных алгебраических уравнений [4];
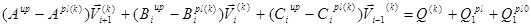 (4)
(4)
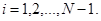
если
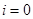 то
то
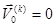 (5)
(5)
Если 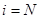 то
то
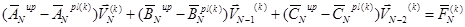 (6)
(6)
Алгоритм вычисления функции пластичности 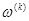 и вектор функции
и вектор функции 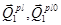 подробно описаны в работах [2,4].
подробно описаны в работах [2,4].
Для решения поставленной задачи (4)-(6) применяем метод матричной прогонки с учетом простой итерации.
Процесс итерации прекращается при выполнении условии.
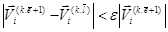
Где
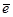 -число итерации
-число итерации
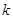 -число нагруженные
-число нагруженные
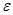 -точность вычисления
-точность вычисления
Для реализации разработанного алгоритма составлена модифицированная программа на объектно-орентированном языке Delphi
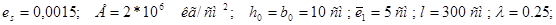
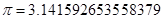 ;
; 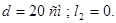
Цель задач — исследование численной сходимости. Поэтому в таблице приводятся экстремальные значения решения краевых задач и расчетных величин, полученных при переменных нагруженных. Для исследования численной задач решается с разным количеством узла сетки
Анализ результатов показывает, что полученные значения параметров на каждом упруго-пластическом нагружённые.
|
|
|
||||||
|
N=50 |
N=90 |
N=100 |
N=110 |
N=50 |
N=90 |
N=100 |
N=110 |
|
-0.04770 |
-0.04055 |
-0.03927 |
-0.03859 |
15844122.9 |
27314428.5 |
29990939.0 |
32613261.5 |
|
0.04696 |
0.03736 |
0.03582 |
0.03453 |
-15148820.2 |
-27326818.0 |
-30722581.4 |
-34126317.1 |
|
-0.04702 |
-0.03752 |
-0.03598 |
-0.03470 |
15138710.3 |
27305817.0 |
30710240.3 |
34113215.3 |
|
0.04701 |
0.03751 |
0.03597 |
0.034469 |
-1513712.2 |
-27304817.1 |
-30710130.2 |
-34112213.1 |
|
|
|
||||||
|
-0.09981 |
-0.08993 |
-0.08845 |
-0.08724 |
-33059.2 |
-32494.6 |
-32394.8 |
-32310.5 |
|
0.09868 |
0.08544 |
0.08327 |
0.088145 |
31169.77 |
30426.80 |
30310.80 |
30213.58 |
|
-0.09878 |
-0.08569 |
-0.08353 |
-0.08171 |
-31056.71 |
-30414.70 |
-30383.81 |
-30298.91 |
|
0.09876 |
0.08567 |
0.08351 |
0.08170 |
31045.78 |
30413.81 |
30301.70 |
30288.92 |
|
|
|
||||||
|
0.07075 |
0.07822 |
0.07931 |
0.08020 |
-11600207.1 |
-26190916 |
-27215410 |
-28233232 |
|
-0.07178 |
-0.08140 |
-0.08294 |
-0.08422 |
10803681.1 |
14757449.6 |
15831598.5 |
16901916.3 |
|
0.07173 |
0.08123 |
0.08277 |
0.08405 |
-10812581.2 |
-14743421.3 |
-15821620.1 |
-16901711.3 |
|
-0.07174 |
-0.08124 |
-0.8227 |
-0.08406 |
10811471.5 |
14742421.3 |
15832177.3 |
16900721.5 |
|
|
|
||||||
|
0.13303 |
0.14492 |
0.14666 |
0.14808 |
44801.76 |
51346.78 |
52254.51 |
52980.39 |
|
-013474 |
-0.14979 |
-0.15218 |
-0.15418 |
-43547.32 |
-51473.64 |
-52745.81 |
-53806.67 |
|
0.13463 |
0.14952 |
0.15191 |
0.15391 |
43701.30 |
51335.62 |
52244.51 |
53814.52 |
|
-0.13466 |
-0.14955 |
-0.15193 |
-0.15393 |
-43711.40 |
-51463.54 |
-52795.71 |
-53813.51 |
|
|
|
||||||
|
-0.000146 |
-0.000147 |
-0.0001472 |
-0.000147 |
-2006.3 |
-2752.7 |
-2924.7 |
-3093.8 |
|
0.000146 |
0.000147 |
0.0001474 |
0.000147 |
2616.0 |
3770.1 |
4034.4 |
4287.8 |
|
-0.000146 |
-0.000147 |
-0.0001474 |
-0.000147 |
-2617.1 |
-3770.1 |
-4032.3 |
-4286.8 |
|
0.000146 |
0.000147 |
0.0001474 |
0.000147 |
2618.2 |
3770.1 |
4031.3 |
4285.8 |
|
|
|
||||||
|
0.80942 |
0.80001 |
0.798486 |
0.797222 |
6.7581 |
6.3340 |
6.2700 |
6.2181 |
|
0.76161 |
0.76530 |
0.7658314 |
0.766265 |
5.0429 |
5.1435 |
5.1558 |
5.1704 |
|
0.76202 |
0.76591 |
0.7664998 |
0.766978 |
5.0537 |
5.1600 |
5.1771 |
5.1906 |
|
0.76201 |
0.76581 |
0.7664720 |
0.766950 |
5.0535 |
5.1600 |
5.1763 |
5.1898 |
При 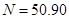 ; перемещения
; перемещения 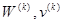 ; углы поворота
; углы поворота 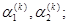 изгибающий момент
изгибающий момент 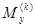 и поперечное усилие
и поперечное усилие 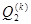 совпадают до одного знака точности, угол закручивания
совпадают до одного знака точности, угол закручивания 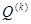 — до двух-трех знаков.
— до двух-трех знаков.
Крутящий 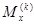 и изгибающий моменты
и изгибающий моменты 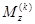 , а также поперечное усилие
, а также поперечное усилие 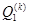 в данном количестве узлов сетки не имеют сходимости. Далее увеличение шага сетки приводит к улучшению сходимости указанных параметров. Например
в данном количестве узлов сетки не имеют сходимости. Далее увеличение шага сетки приводит к улучшению сходимости указанных параметров. Например
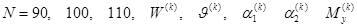 имеют сходимость до двух и более знаков точности, а
имеют сходимость до двух и более знаков точности, а 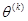 — до трех и солее;
— до трех и солее; 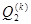 ,
, 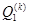 ,
, 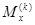 — до одного-двух знаков точности (таблица). Во всех шагах сетки функция пластичности
— до одного-двух знаков точности (таблица). Во всех шагах сетки функция пластичности 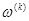 и интенсивности
и интенсивности 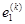 сходятся до двух-трех и более знаков точности. Алгоритм с заданным модулем сходимости, построенный на основа метод конечных разностей, требует четырех итераций для каждого нагруженные (для
сходятся до двух-трех и более знаков точности. Алгоритм с заданным модулем сходимости, построенный на основа метод конечных разностей, требует четырех итераций для каждого нагруженные (для 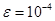 ).
).
Исходя из анализа численной сходимости параметров, можно сделать вывод, что для ведения серийного счета пространственных стрежней при переменных упруго — пластических нагружённых можно принять число узлов 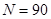 .
.
Литература:
1. Москвитин В. В. Пластичность при переменных нагружённых. Изд-ваб, МГУ 1965.
2. Кабулов В.К, Алгоритимизация в теории упругости и деформацион теории пластичности, Ташкент, “Фан”, 1966 г.
3. Олимов М, Жакбаров О.О, Ирискулов Ф.С,. Алгоритм решения прикладных задач для обыкновенных дифференциальных уравнений четвертого порядка с методом дифференциальной прогонки «Молодой учёный» Ежемесячный научный журнал № 6(86) / 2015 г. часть 2
4. Олимов М., Ирскулов С., К. Исманова, А. Имомов., «Численные методы и алгоритмы» учебное пособие «Наманган» 2013 йил