С каждым годом стремительно увеличивается число компаний и государственных учреждений по всему миру, прибегающих к различным компьютерным технологиям при принятии сложных управленческих решений. Благодаря имитационным моделям в экономике стало возможным оценить результат тех или иных потенциальных решений насущных проблем, не испытывая их в реальности. [1]
Само по себе имитационное моделирование (ситуационное моделирование) представляет собой метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По изученным данным можно получить достаточно устойчивую статистику. [2]
Иными словами, имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему. Благодаря имитационному моделированию проводятся эксперименты с целью получения информации об этой системе. Ситуационное моделирование является частным случаем математического моделирования. Оно используется для испытания модели на компьютере в целях проектирования, анализа и оценки функционирования объекта.
Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае аналитическая модель заменяется имитатором или имитационной моделью.
Имитационным моделированием иногда называют получение частных численных решений сформулированной задачи на основе аналитических решений или с помощью численных методов. [5]
Структура имитационного моделирования представляется последовательно-циклической. Последовательность определяется тем, что процесс имитационного моделирования можно разбить на ряд этапов, выполнение которых осуществляется последовательно от предыдущего к последующему. Цикличность проявляется в необходимости возвращения к предыдущим этапам и повторении уже однажды пройденного пути с измененными в силу необходимости данными и параметрами модели (Рис. 1.).
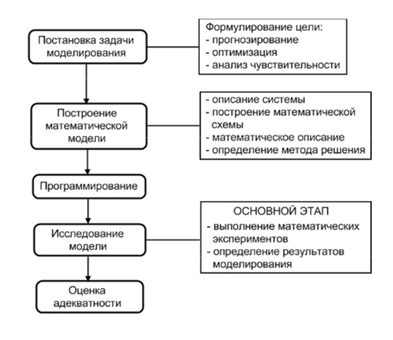
Рис. 1. Этапы имитационного моделирования при исследовании сложной проблемной ситуации
Первый этап необходим для того, чтобы была оценена потребность изучения объекта или проблемы, возможность и способы решения задачи, ожидаемые результаты. Очень часто к этому этапу возвращаются после окончания исследования модели и обработки результатов для изменения постановки задачи, а иногда и самой цели моделирования.
Второй этап — формализация описания моделируемого объекта на основе выбранной теоретической базы. Здесь на естественном языке дается описание состава исследуемого объекта, взаимодействия между элементами объекта и объекта с внешней средой. На этом этапе осуществляется и проверка полученной моделирующей программы на соответствие ее той теоретической схеме, которая была положена в основу формального описания объекта моделирования. Этот процесс часто называют верификацией модели. Заканчивается второй этап проверкой соответствия имитационной модели свойствам реальной системы с помощью перехода на математическую структуру. Если этого нет, то следует снова вернуться к моменту формализации модели, чтобы провести коррекцию в определении теоретической базы модели.
Третий этап — проведение исследования на разработанной модели путем «прогона» ее на ЭВМ. Перед началом исследования полезно составить такую последовательность «прогонов» модели, которая позволила бы получить необходимый объем информации при заданном составе и достоверности исходных данных. Далее на основе разработанного плана эксперимента осуществляют «прогоны» имитационной модели на ЭВМ. В конце этапа осуществляется обработка результатов с целью представления их в виде, удобном для анализа.
Четвертый этап представляет собой анализ результатов исследования. На этом этапе определяются те свойства реальной системы, которые наиболее важны для исследователя. На основе анализа результатов подготавливаются окончательные выводы по проведенному моделированию.
Пятый этап является заключительным. На этом этапе формулируются окончательные выводы и разрабатываются рекомендации по использованию результатов моделирования для достижения поставленных целей. Часто на основе этих выводов возвращаются к началу процесса моделирования для необходимых изменений в теоретической и практической части модели и повторным исследованиям с измененной моделью. В результате нескольких подобных циклов получают имитационную модель, наилучшим образом удовлетворяющую поставленным задачам.
Таким образом, метод имитационного моделирования при исследовании сложной проблемной ситуации предполагает выполнение пяти этапов.
Имитационные модели позволяют проверить, правильно ли мы понимаем процессы в исследуемом объекте, и выявить в различных конкретных случаях параметры порядка. Знание последних и дает возможность строить простые модели сложных явлений. [3]
Основными достоинствами метода имитационного моделирования (ИМ), проявляющимися при исследовании сложных систем являются:
- возможность исследования особенностей процесса функционирования системы в любых условиях.
- применение ЭВМ сокращает продолжительность испытаний по сравнению с натурным экспериментом.
- ИМ позволяет при своём построении использовать результаты натурных испытаний при эксплуатации системы для проведения дальнейших исследований.
- ИМ обладает известной гибкостью варьирования параметров и структуры моделируемой системы, что важно с точки зрения поиска оптимального варианта системы.
- ИМ сложных систем часто является единственным практически реализуемым методом исследования процесса функционирования таких систем на этапе их проектирования.
Имитационному моделированию присущ и следующий существенный недостаток: решение, полученное в результате анализа имитационной модели, всегда носит частный характер, так как оно соответствует фиксированным значениям параметров системы, начальных условий и воздействий внешней среды. Поэтому для полного анализа характеристик процесса функционирования системы приходится многократно воспроизводить имитационный эксперимент, варьируя исходные данные задачи. [4]
При имитационном моделировании так же, как и при любом другом методе анализа и синтеза системы, весьма существенным является вопрос эффективности.
Эффективность имитационного моделирования может оцениваться:
1. Точностью моделирования (погрешность описания реального физического процесса подобными математическими соотношениями + погрешность реализации приближённого моделирования).
2. Затраты машинного времени = Время ввода, вывода данных + Время проведённых вычислительных операций. [3]
Итак, развитие области информационных технологий и её преобразующая роль в управлении общественными процессами сделали область их технологий катализатором управленческого прогресса. Благодаря им появилась возможность просматривать решение сложившихся социально-экономических и финансовых ситуаций, не теряя при этом огромные материальные и временные ресурсы. К тому же, воплощать в жизнь различные модели по решению экономических и социальных проблем с помощью компьютерного имитирования дает возможность выбрать наиболее оптимальный вариант.
Литература:
1. Электронный ресурс: http://www.fa.ru/projects/mknrsa/skireports
2. Строгалев В. П., Толкачева И. О. Имитационное моделирование. — МГТУ им. Баумана, 2008. — С. 697–737. — ISBN 978–5-7038–3021–5.
3. Электронный ресурс: http://otherreferats.allbest.ru/emodel/00133125_0.html Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов. — М., ЮНИТИ-ДАНА, 2001 г.
4. Начинающий трейдер. Еженедельный электронный журнал. Оценка торговых систем методами Монте-Карло, выпуск 35 от 19 сентября 2010 http://pressa.ru/import/upload/e831b091389b329f3a863b9c338dc809.pdf
5. Ермаков С. М., Михайлов Г. А. Курс статистического моделирования. — Москва: Наука, 1976 г. http://multidollar.ru/kolehn/coj_evgenij_modelirovanie_i_upravlenie_v_ehkonomike.html
6. Электронный ресурс: http://allrefs.net/c12/458he/p32/?full







