В настоящей работе методами имитационного моделирования исследуется влияние входных погрешностей в начальных данных и естественных ограничениях по содержанию компонентов смесей на расчетные параметры оптимальных по свойству и стоимости составов сухих строительных смесей. Приводятся результаты имитационного моделирования соответствующим модельным и реальным системам [1–3].
Ключевые слова:имитационное моделирование, интегральный критерий, параметры стоимости, функции минимизации MathCAD15.
In the present work, simulation methods we investigate the effect of input errors in the initial data and the natural restrictions on the content of components of mixtures on the optimal design parameters for the property and the cost of dry building mixtures. The results of simulation corresponding model and real systems [1–3].
Key words: imitational modeling, integral criterion, the parameters of the cost function minimization MathCAD 15.
В работе [4] предложен новый метод и алгоритм получения оптимальных значений компонентов составов строительных материалов из условия минимальной стоимости и выполнение естественных ограничений качества строительной продукции на основе получения оптимальных значений параметров стоимостного интегрального критерия качества методами имитационного моделирования. Предложенный алгоритм в качестве ключевого звена включает в себя задачу определения оптимального состава 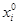 при заданных стоимостях
при заданных стоимостях 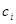 и ограничениях [1] из следующего уравнения
и ограничениях [1] из следующего уравнения
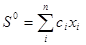 (1).
(1).
Таким образом, для найденного оптимального 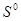 на первом этапе решения задачи, необходимо определить соответствующие оптимальные значения
на первом этапе решения задачи, необходимо определить соответствующие оптимальные значения 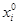 . Сводя эту задачу к задаче квадратичного программирования — нахождения минимума функции (2) по вектору (
. Сводя эту задачу к задаче квадратичного программирования — нахождения минимума функции (2) по вектору (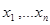 ):
):
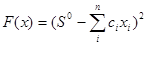 (2)
(2)
можно утверждать, что она имеет единственное решение. Мы отдаем себе отчет, что в силу вида целевой функции минимизации, а также возможной ее «овражистости», многое зависит от начальных приближений [5], поэтому в выборе начальных приближений мы использовали различные варианты. Учитывая характерные значения для 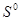 и ограничений необходимо получить реальные практические оценки для устойчивости и коридоров погрешностей в находимых xi в зависимости от погрешностей и ограничений входных данных. Для этого нами использовался классический подход имитационного моделирования [6], использованный авторами в решении задач строительства, напр. [7–8]. В качестве модельных выбиралось следующее: уравнение (1), значения стоимости
и ограничений необходимо получить реальные практические оценки для устойчивости и коридоров погрешностей в находимых xi в зависимости от погрешностей и ограничений входных данных. Для этого нами использовался классический подход имитационного моделирования [6], использованный авторами в решении задач строительства, напр. [7–8]. В качестве модельных выбиралось следующее: уравнение (1), значения стоимости 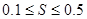 с ограничениями
с ограничениями 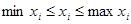 , и значениями
, и значениями 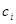 (табл.1.), характерными для реальных многокомпонентных систем:
(табл.1.), характерными для реальных многокомпонентных систем:
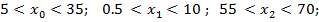
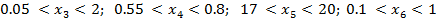 (3)
(3)
Точные модельные значения xi в уравнении (1) и ограничениях (3) «портилось» на 3 %, 5 %, 10 %, 20 %, 30 %, затем по «испорченным» данным находились восстановленные значения компонентов. Далее подсчитывались среднее значение 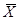 и относительный эмпирический стандарт
и относительный эмпирический стандарт
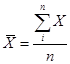 ,
, 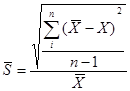 (4)
(4)
n- количество серий расчетов, X — восстановленные значения компонентов.
Для оценки погрешности оптимальных компонентов смеси брался конкретный пример, условной стоимостью S=0.254 на 100г. навески. С заданными ограничениями по компонентам
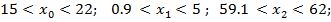
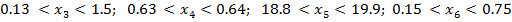 (5)
(5)
Таблица 1
Цены компонентов
|
Компоненты |
Цена |
|
Известь, кг |
5 |
|
ГСК, кг |
13 |
|
песок, кг |
0.15 |
|
С-З, кг |
49 |
|
Neolith, кг |
75 |
|
наполнитель: кг желтый синий |
175 230 |
и точным начальным приближением xi
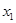 =15.24,
=15.24, 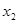 =4.57,
=4.57, 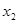 =59.45,
=59.45, 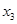 =0.14,
=0.14, 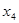 =0.64,
=0.64, 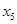 =19.81,
=19.81, 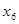 =0.15.
=0.15.
Далее при помощи функции rnd среды mathcad начальное приближение xi «портилось» на 3 %, 5 %, 10 %, 20 %, 30 % и просчитывалось 1000 раз. Из полученных результатов подсчитывалась среднее значение 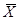 и относительный эмпирический стандарт рис. (1, 2)
и относительный эмпирический стандарт рис. (1, 2)
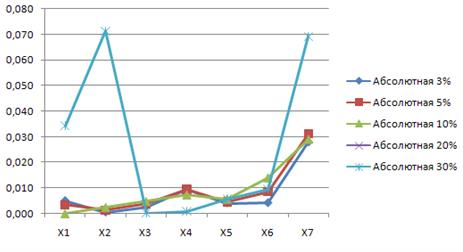
Рис.1. Среднее значение 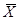 имитационное выборки n=1000.
имитационное выборки n=1000.
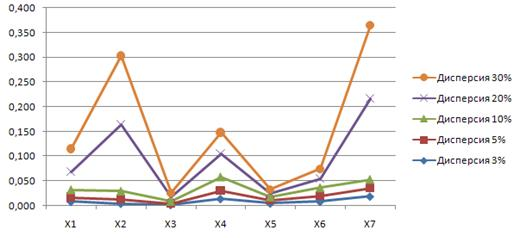
Рис. 2. Относительный эмпирический стандарт n=1000
Для более детального анализа выберем компоненты xi, которые имеют максимальные, минимальные и средние значения Рис. (3,4).
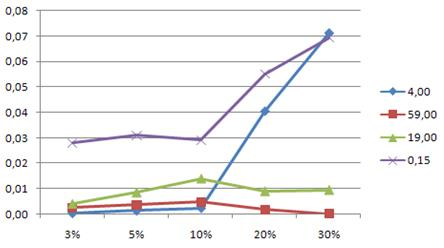
Рис.3. Среднее значение 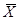 имитационное выборки n=1000
имитационное выборки n=1000
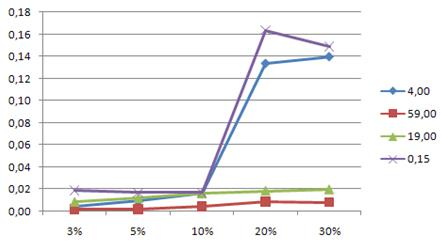
Рис. 4. Относительный эмпирический стандарт n=1000
По графикам можно определять погрешность оценок содержания компонентов xi при различных погрешностях начальных приближений (3 %, 5 %, 10 %, 20 %, 30 %).
Несмотря на большую начальную погрешность, конечные результаты варьируются в пределах 7 % по средним значениям 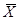 и до 16 % относительного эмпирического стандарта, это связано с тем, что допустимый диапазон содержательных ограничений на компонентный состав, меньший имитационной погрешности [9].
и до 16 % относительного эмпирического стандарта, это связано с тем, что допустимый диапазон содержательных ограничений на компонентный состав, меньший имитационной погрешности [9].
В рассматриваемом случае были получены следующие значения. Состав 0.254.
Таблица 2
Полученные компоненты
|
известь, % |
ГСК, % |
песок, % |
С-З, % |
Neolith, % |
H20, % |
наполнитель, % |
стоимость, удельных ед. |
|
15.276 |
4.578 |
59.466 |
0.14 |
0.64 |
19.822 |
0.15 |
0,254 |
Литература:
1. Логанина В. И., Камбург В. Г., Бодажков Н. Ю., Макарова Л. В. Оптимизация состава сухих строительных смесей с учетом их стоимости. Известия высших учебных заведений. Строительство. 2014. № 6 (666). С. 44–50.
2. Kamburg V. G., Bodazhkov N. Y., Loganina V. I., Makarova L. V. Method of building optimization of composites based on the criterion analysis // journal of innovative technology and education Vol. 2, HIKARI Ltd, Bulgaria 2014.
3. Kolodyazhny S. A., Kavygin A. A., Kamburg V. G. Experimental research of the plate cross-counterflow heat exchanger in freezing conditions.Scientific herald of the voronezh state university of architecture and civil engineering. construction and architecture.2014. № 4 (24). С. 7–16.
4. Камбург В. Г., Бодажков Н. Ю., Агафонкина Н. В. Управление качеством строительных технологий на основе обобщенного критерия качества. Молодой ученый. 2015. — №92 (12).
5. Пшеничный Б. Н., Данилин Ю. М. Численные методы в экстремальных задачах [Текст]. –М.: Наука, 1975. — С. 320.
6. Строгалев В. П., Толкачева И. О. Имитационное моделирование. — МГТУ им. Баумана, 2008. — С. 697–737.
7. Kamburg V. G., Shitov V. V. Mathematical modeling and intensification of condensation gravity fine air filter operation.Scientific Herald of the Voronezh State University of Architecture and Civil Engineering. Construction and Architecture. 2011. № 2. -С. 35–44.
8. Логаніна В., Камбург В. Г., Учаева Т. В. Удосконалення системи контролю якості будівельних матеріалів та виробів. Технологический аудит и резервы производства. 2012. Т. 1. № 1 (3). -С. 13–16.
9. Корниенко В. С. Математическая статистика. Решение задач по теме: «Проверка статистических гипотез». Методическая разработка [Текст]. Волгогр. гос. с.-х. акад. Волгоград, 2010. –С.68.







