В работе предложено решать задачу об оптимальной стабилизации для функционально-дифференциального уравнения на основе функционалов Ляпунова со знакопостоянной производной. Для этого используется метод предельных уравнений.
Ключевые слова:оптимальная стабилизация, метод предельных уравнений, функционалов Ляпунова со знакопостоянной производной.
В середине 20-го столетия получила большое развитие теория оптимальных процессов в управляемых динамических системах, которая охватывает широкий круг проблем прикладного характера. Среди этих проблем важное техническое значение имеет поставленная А. М. Летовым [1] проблема аналитического конструирования регуляторов, относящаяся к задачам синтеза оптимальных систем с обратной связью. Развивая идеи А. М. Летова, Н. Н. Красовский разработал теорию оптимальной стабилизации управляемых движений [2]. Это — задача о построении регулирующих воздействий, которые обеспечивают устойчивое осуществление желаемого движения при наилучшем возможном качестве переходного процесса. Задача об оптимальной стабилизации тесно смыкается с общей задачей об устойчивости движения и является дальнейшим развитием проблемы устойчивости в приложении к теории управляемых систем. Методы исследования проблем оптимальной стабилизации переплетаются с классическими методами теории устойчивости Ляпунова. Подход Н. Н. Красовского с успехом применяется при решении оптимальных задач аналитического конструирования регуляторов для линейных систем. Однако при применении этой теории к нелинейным системам с целью получения синтезирующего управления в замкнутой форме возникают серьезные математические трудности, источником которых является отсутствие универсального способа построения функционала Ляпунова в каждом конкретном случае. Ведь, как известно, задача об оптимальной стабилизации движения управляемой системы на бесконечном интервале времени сводится к отысканию оптимального функционала Ляпунова и оптимальных управляющих воздействий, удовлетворяющих уравнению в частных производных типа Беллмана, которое необходимо решить с учетом дополнительного неравенства. В работе [3] предложено решать задачу об оптимальной стабилизации для обыкновенных дифференциальных уравнений на основе функций Ляпунова со знакопостоянной производной. В данной работе предлагается аналогичное решение для функционально-дифференциального уравнения.
Отметим, что структура функционала качества и выбор его коэффициентов не являются фиксированными и могут, вообще говоря, выбираться с определенным произволом, так как основная задача состоит не в минимизации конкретного функционала, а в построении стабилизирующего управления.
1. Постановка задачи об оптимальной стабилизации.
Пусть 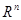 — линейное действительное пространство
— линейное действительное пространство 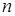 - векторов
- векторов 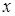 ,
, 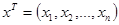 с нормой
с нормой 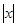 ,
, 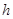 > 0 — действительное число,
> 0 — действительное число, 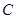 — банахово пространство непрерывных функций
— банахово пространство непрерывных функций 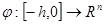 c нормой
c нормой 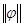 = sup
= sup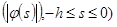 , для
, для 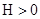
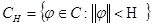 , если
, если 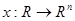 есть непрерывная функция, тогда для
есть непрерывная функция, тогда для 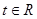 функция
функция 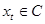 определяется равенством
определяется равенством 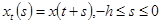 , под
, под 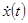 понимается правосторонняя производная.
понимается правосторонняя производная.
Рассматривается управляемая система, движение которой описывается функционально-дифференциальным уравнением запаздывающего типа:
(1.1) 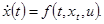
Здесь 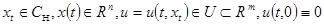 , где
, где 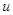 есть управляющее воздействие,
есть управляющее воздействие, 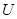 — некоторый класс допустимых управлений;
— некоторый класс допустимых управлений; 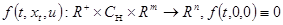 есть непрерывное отображение, удовлетворяющее в
есть непрерывное отображение, удовлетворяющее в 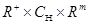 условиям существования, единственности и непрерывной зависимости решений (1.1) от начальных данных.
условиям существования, единственности и непрерывной зависимости решений (1.1) от начальных данных.
Пусть 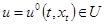 есть некоторое выбранное управляющее воздействие, под действием которого уравнения (1.1) принимают вид:
есть некоторое выбранное управляющее воздействие, под действием которого уравнения (1.1) принимают вид:
(1.2) 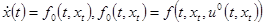 .
.
Предполагаем, что правая часть системы (1.2) удовлетворяет предположениям 1.1–1.3 [4]. Тогда можно построить семейство предельных уравнений к (1.2):
(1.3) 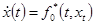 ,
,
где 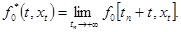
Рассмотрим функционал:
(1.4) 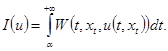
Здесь 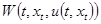 есть некоторый непрерывный неотрицательный функционал переменных
есть некоторый непрерывный неотрицательный функционал переменных 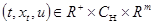 , характеризующий качество переходного процесса. Выбор
, характеризующий качество переходного процесса. Выбор 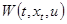 в конкретной прикладной задаче осуществляется с учетом особенностей ее постановки, ограничения ресурсов управления, требования к оценке переходного процесса и возможностях формы или способа решения задачи.
в конкретной прикладной задаче осуществляется с учетом особенностей ее постановки, ограничения ресурсов управления, требования к оценке переходного процесса и возможностях формы или способа решения задачи.
Введем обозначения: 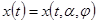 есть движение, удовлетворяющее начальному условию
есть движение, удовлетворяющее начальному условию 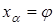 и порождаемое управляющим воздействием
и порождаемое управляющим воздействием 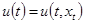 , где
, где 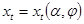 . Соответственно
. Соответственно 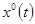 порождается управляющим воздействием
порождается управляющим воздействием 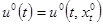 .
.
Определение 1.1. Задача оптимальной стабилизации заключается в нахождении управляющего воздействия 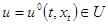 , обеспечивающего асимптотическую устойчивость невозмущенного движения
, обеспечивающего асимптотическую устойчивость невозмущенного движения 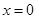 , и такого что по сравнению с любыми другими управляющими воздействиями
, и такого что по сравнению с любыми другими управляющими воздействиями 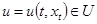 , решающими задачу о стабилизации движения
, решающими задачу о стабилизации движения 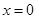 , для всех
, для всех 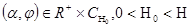 выполняется неравенство:
выполняется неравенство:
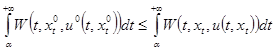
при условиях 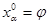 .
.
Замечание 1.1. Область 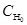 в определении 1.1 принята независимой от
в определении 1.1 принята независимой от 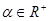 .
.
2. Теорема об оптимальной стабилизации на основе знакоопределенного функционала Ляпунова
Обозначим через 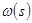 непрерывную, строго монотонно возрастающую функцию
непрерывную, строго монотонно возрастающую функцию 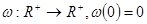 .
.
Пусть 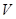 :
: 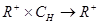 есть непрерывный знакоопределенный функционал Ляпунова:
есть непрерывный знакоопределенный функционал Ляпунова: 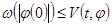 .
.
Определение 2.1. Пусть 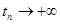 есть некоторая последовательность. Для каждого
есть некоторая последовательность. Для каждого 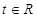 и
и 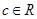 определим множество
определим множество 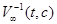 следующим образом: точка
следующим образом: точка 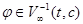 , если существует подпоследовательность
, если существует подпоследовательность 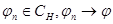 , такая, что:
, такая, что: 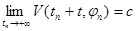 .
.
Введем следующее выражение:
(2.1) 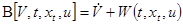
В силу того, что 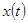 зависит от
зависит от 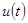 , то
, то 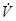 также зависит от
также зависит от 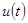 . Выражение (2.1) совпадает и близко по смыслу с соответствующим выражением Беллмана в методе динамического программирования. Предположим, что
. Выражение (2.1) совпадает и близко по смыслу с соответствующим выражением Беллмана в методе динамического программирования. Предположим, что 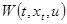 удовлетворяет вышеупомянутым предположениям 1.1, 1.3.
удовлетворяет вышеупомянутым предположениям 1.1, 1.3.
Теорема 2.1. Предположим, что в некоторой окрестности 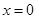 для системы
для системы 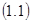 можно найти непрерывный функционал
можно найти непрерывный функционал 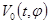 и управляющее воздействие
и управляющее воздействие
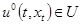 , удовлетворяющие условиям:
, удовлетворяющие условиям:
1) движение системы 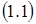 из некоторой окрестности
из некоторой окрестности 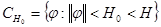 равномерно ограничены областью
равномерно ограничены областью 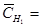
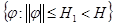 ;
;
1. 2) 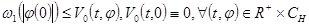 ;
;
2) имеет место тождество: 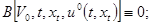
3) существуют предельная пара 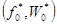 с множеством
с множеством 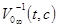 , такие, что для каждого значения
, такие, что для каждого значения 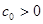 множество
множество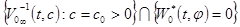 не содержит решений уравнения
не содержит решений уравнения 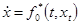 .
.
4) для всех 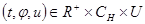 справедливо неравенство:
справедливо неравенство: 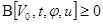 ;
;
5) для каждого движения 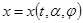 , соответствующего управлению
, соответствующего управлению 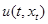 ,
, 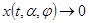 ,
, 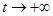 , имеет место свойство:
, имеет место свойство:
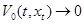 ,
, 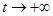 .
.
Тогда управляющее воздействие 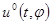 решает задачу об оптимальной стабилизации невозмущенного движения (1.1), а именно: при
решает задачу об оптимальной стабилизации невозмущенного движения (1.1), а именно: при 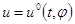 решение
решение 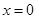 асимптотически устойчиво равномерно по
асимптотически устойчиво равномерно по 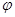 с областью притяжения
с областью притяжения 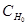 и для каждого соответствующего движения
и для каждого соответствующего движения 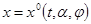 ,
, 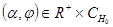 выполняется:
выполняется:
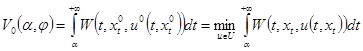 .
.
Доказательство. Согласно условию 3) теоремы:
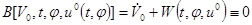 .
.
Следовательно:
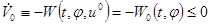 .
.
Из теоремы 3.1.2 [5], в силу условий 1), 2) и 4) теоремы, получаем, что решение 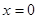 уравнения (1.1) асимптотически устойчиво равномерно по
уравнения (1.1) асимптотически устойчиво равномерно по 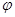 с областью притяжения
с областью притяжения 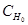 . Таким образом, для каждого движения системы (1.1) при
. Таким образом, для каждого движения системы (1.1) при 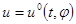 имеем:
имеем: 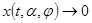 ,
, 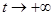 ,
, 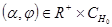 . Из условия 4), кроме того, следует, что для каждого решения
. Из условия 4), кроме того, следует, что для каждого решения 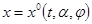 ,
, 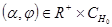 выполняется:
выполняется:
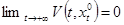 .
.
Из условия 3) теоремы следует, что:
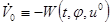 .
.
Интегрируем последнее тождество по 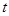 от
от 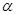 до
до 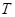 , получаем:
, получаем:
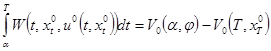 .
.
Переходим к пределу при 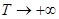 , получаем:
, получаем:
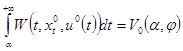 .
.
Пусть 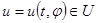 есть любое другое управляющее воздействие, для которого соответствующее движение
есть любое другое управляющее воздействие, для которого соответствующее движение 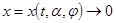 ,
, 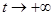 ,
, 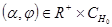 . В силу условия 5) теоремы следует неравенство:
. В силу условия 5) теоремы следует неравенство:
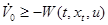 .
.
Интегрируя последнее неравенство по 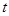 от
от 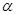 до
до 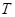 и переходя к пределу при
и переходя к пределу при 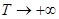 из условия 6) теоремы, получаем:
из условия 6) теоремы, получаем:
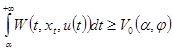 .
.
Теорема доказана.
Теорема 2.1 дополняет некоторые результаты работы [6].
Замечание 2.1. Из доказательства теоремы 2.1 видно, что важным условием является условие 6) теоремы, так как из первых пяти условий теоремы, вообще говоря, не следует, что 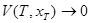 ,
, 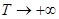 когда,
когда, 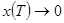 ,
, 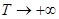 . В следующей теореме [6] показано, что условие 6) можно заменить на условие существования бесконечно малого высшего предела у функционала
. В следующей теореме [6] показано, что условие 6) можно заменить на условие существования бесконечно малого высшего предела у функционала 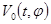 и при этом видоизменить условие 1.
и при этом видоизменить условие 1.
Теорема 2.2. Предположим, что в некоторой окрестности 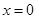 для системы
для системы 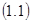 можно найти непрерывный функционал
можно найти непрерывный функционал 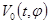 и управляющее воздействие
и управляющее воздействие
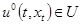 , удовлетворяющие условиям:
, удовлетворяющие условиям:
1) 1) 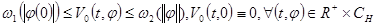 ;
;
2) имеет место тождество: 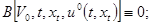
3) каждая предельная пара 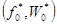 такова, что множество
такова, что множество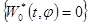 не содержит решений уравнения
не содержит решений уравнения 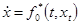 , кроме нулевого;
, кроме нулевого;
4) для всех 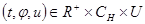 справедливо неравенство:
справедливо неравенство: 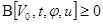 ;
;
Тогда управляющее воздействие 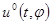 решает задачу об оптимальной стабилизации невозмущенного движения (1.1), а именно: при
решает задачу об оптимальной стабилизации невозмущенного движения (1.1), а именно: при 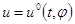 решение
решение 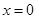 равномерно асимптотически устойчиво с областью притяжения
равномерно асимптотически устойчиво с областью притяжения 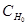 и для каждого соответствующего движения
и для каждого соответствующего движения 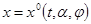 ,
, 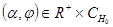 выполняется:
выполняется:
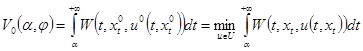 .
.
Доказательство. Согласно условию 2) теоремы:
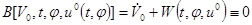 .
.
Следовательно:
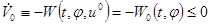 .
.
Из теоремы 3.1.3 [5], в силу условий 1) — 3) теоремы, получаем, что решение 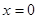 уравнения (1.1) равномерно асимптотически устойчиво с областью притяжения
уравнения (1.1) равномерно асимптотически устойчиво с областью притяжения 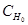 . Таким образом, для каждого движения системы (1.1) при
. Таким образом, для каждого движения системы (1.1) при 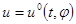 имеем:
имеем: 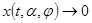 ,
, 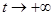 ,
, 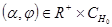 .
.
Из условия 2) теоремы следует, что:
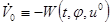 .
.
Интегрируем последнее тождество по 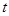 от
от 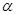 до
до 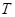 , получаем:
, получаем:
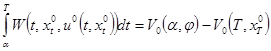 .
.
Переходим к пределу при 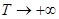 , учитывая, что функционал
, учитывая, что функционал 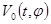 допускает бесконечно малый высший предел, получаем:
допускает бесконечно малый высший предел, получаем:
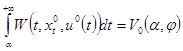 .
.
Пусть 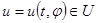 есть любое другое управляющее воздействие, для которого соответствующее движение
есть любое другое управляющее воздействие, для которого соответствующее движение 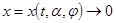 ,
, 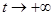 ,
, 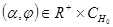 . В силу условия 4) теоремы следует неравенство:
. В силу условия 4) теоремы следует неравенство:
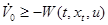 .
.
Интегрируя последнее неравенство по 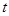 от
от 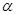 до
до 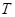 и переходя к пределу при
и переходя к пределу при 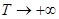 из условия 1) теоремы, получаем:
из условия 1) теоремы, получаем:
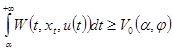 .
.
Теорема доказана.
Литература:
1. Летов А. М. Аналитическое конструирование регуляторов//АиТ. –1960. — Т.21. –№ 4–6.; 1961. — Т. 22. — № 4.; 1962. — Т.23. — № 11.
2. Красовский Н. Н. Проблемы стабилизации управляемых движений. В кн.:Малкин И. Г. «Теория устойчивости движения», Дополнение 4. –М.:Наука, 1966. — С. 475–515.
3. Ким Е. Б. О моделировании нелинейной управляемой системы //Социально-экономические и технические системы. — 2006. — № 3(19) — Режим доступа: http://kampi.ru/sets/.
4. Павликов С. В. О стабилизации систем, моделируемых функционально-дифференциальными уравнениями второго порядка // Социально-экономические и технические системы. — 2006. — 1(17). — Режим доступа: http://kampi.ru/sets/.
5. Павликов С. В. Метод функционалов Ляпунова в задачах устойчивости и стабилизации. Набережные Челны. — Изд-во Института управления. — 2010. — 394 с.
6. Павликов С. В., Савин И. А., Емельянов Д. В. К методу функционалов Ляпунова в задаче об оптимальной стабилизации управляемых систем // Вестник КГТУ им. А. Н. Туполева. — 2013. — № 4. — С. 170–176.







