В статье рассмотрены вопросы рациональной организации процесса выпарки и пути интенсификации. Как известно, тепловые и массообменные процессы являются самыми энергозатратными. Снижение длительности этих процессов способствует повышению производительности, снижению энергозатрат и себестоимости продукции.
Ключевые слова: математическое моделирование, выпарка, повидло, вторичное сырье, концентрирования растворов, сахаросодержащая масса, фугат.
Значительное количество производственных процессов пищевой промышленности осуществляется в емкостном оборудовании. Это процессы нагрева, охлаждения, смешения жидкостей, разбавления растворов, растворения гранулированных или сыпучих материалов, кристаллизации, отгонки, химические превращения, догрузка и частичная разгрузка, а также различные комбинации этих процессов.
Как правило, все эти операции протекают в нестационарных температурных режимах.
В каждом конкретном случае лимитирующим по длительности может быть тепловой или массообменный процесс. Как правило, лимитирующие процессы бывают и самыми энергозатратными. Снижение длительности лимитирующих процессов повышает производительность оборудования, снижает энергозатраты и себестоимость продукции.
Интенсивность тепло и массообменных процессов в жидких продуктах определяется гидродинамической обстановкой в аппарате.
Для получения возможности рациональной организации процессов необходимо иметь четкие указания, которые можно получить путем математического моделирования реальных процессов и аппаратов. Математического моделирование и расчет выпарного аппарата имеют свои специфические особенности. Для этого выпарной аппарат рассматривается в виде системы с определенными показателями и его можно переставлять в следующем виде (Рис.1).

Рис.1.
При переработке вторичного сырья соковых производств и получении пюре и пасты ключевое место занимает концентрирование выпариванием.
Системный подход к решаемой задачи, играющий важную роль, диктует необходимость установления причинно-следственных отношений, характеризующих закономерности протекания процесса. В этом плане целесообразно рассмотреть и проанализировать явления и эффекты процесса выпаривания по всем конструктивным элементам аппарата. Такой анализ подразумевает выявление иерархической структуры процесса как типовой физико-химической системы (ФХС) {А}.
При анализе и синтезе различных вариантов технологических установок для выпарной установки фугата сахаросодержащих масс необходимо располагать уравнениями статики и динамики процесса, входящими в состав статической и динамической математических моделей.
При составлении математической модели процесса концентрирования пульпы сахаросодержащих масс учитываются физико-химические характеристики фаз, особенности конструкций и режимы работы аппаратов, а также принимаются упрощающие допущения.
Общая методика составления математической модели процесса выпарной установки включает следующие этапы: выбор объекта, его изучение, обоснование структурной схемы объекта, составление математического описания составных элементарных явлений и эффектов, которые протекают в отдельных конструктивных узлах и зонах объекта, идентификация параметров математического описания отдельных элементарных процессов, получение полной (или обобщенной) математической модели процесса путем об единения (агрегирования) математических описаний его элементов, выбор методов решения уравнений математической модели объекта и оценка точности расчетов по предлагаемым математическим моделям процессов выпарной установки.
Любая математическая модель (в том числе и модель процесса концентрирования фугата сахаросодержащих масс соковых производств) является приближенным отражением реального процесса. Поэтому для получения наиболее упрощенной, с точки зрения расчета, адекватной реальному процессу математической модели процессов в выпарной установки, необходимо выполнить анализ математических описаний элементарных процессов, протекающих на соответствующих ступенях структуры исследуемого процесса.
Методы системного анализа и математического моделирования технологических процессов подразумевают необходимость раскрытия причинно-следственных связей между элементами изучаемого процесса, занимающими определенное место в иерархической структуре объекта.
На первом этапе реализации системного подхода к исследованию процесса выпаривания сахаросодержащих масс рассмотрим смысловой аспект качественного анализа процесса и с единых позиций выполним последовательное рассмотрение всех аспектов физико-химических явлений и эффектов, объединенных в единую структуру рассматриваемой ФХС. Исходная иерархическая структура процесса представлена как определенная совокупность отдельных элементов процессов концентрирования и теплообмена, на которые удается расчленить изучаемый объект по каналам перемешивания обрабатываемого фугата в отдельных конструктивно выраженных зонах аппарата. Такой подход позволяет положить в основу математической формализации объекта модульный принцип моделирования и обеспечивает возможность получения локальных математических описаний отдельных, далее неделимых элементов процесса. При вариации способов концентрирования и свойств обрабатываемого сырья удельный вес различных ступеней иерархии и отдельных модулей может быть различной. Раскрываемая общая картина исследуемого процесса должна отражать вид подвода тепла, способ удаления вторичного пара, схему взаимодействия потоков в выпарной установки и позволить оценивать вклад каждой ступени иерархии и отдельных явлений и эффектов взаимодействия в собственно процесс удаления влаги из фугата сахаросодержащих масс. На основе такого подхода становится эффективным применение блочного принципа формирования математической модели исследуемого процесса. Итогом такого обобщающего анализа могут быт выявленные более совершенные и экономически оправданные режимы процесса, эффективные способы концентрирования растворов.
Исходя из этих предпосылок к решаемой задаче, процесс выпаривания фугата пульпы вторичного сырья соковых производств необходимо расчленить на элементарные подпроцессы. Далее, путем соответствующего агрегирования локальных математических описаний явлений и эффектов на основе раскрытых связей необходимо сформулировать полную математическую модель всего процесса в целом. Последняя должна отражать основные определяющие особенности протекания изучаемого процесса в условиях установившихся и неустановившихся режимов функционирования выпарной установки.
В мировой практике для концентрирования пульпы с целью получения -пасты широко применяются тепловые аппараты. Принцип их работы основан на выпаривании влаги из продукта путем воздействия на него тепла.
В настоящее время существуют методики расчетов выпарной установки.
Результаты предварительных исследований математической модели процесса получения сахаросодержащих масс выпариванием позволили обосновать целесообразность использования однокорпусной вакуум-выпарной установки.
Структура взаимодействующих при выпаривании фугата сахаросодержащих масс фаз включает элементарные явления, возникающие при движении греющего пара и восходящего по нагреваемой стенке аппарата — пульпы сахаросодержащих масс [А]. Она включает в себя явления, протекающие эффекты и явления, происходящие в результате воздействия тепла глухого пара на пленку нисходящего потока пульпы, и отражает гидродинамическую обстановку в локальных объемах паровой и жидких фаз, а также в аппарате в целом.
Тепловой энергия пара в конструктивных элементах выпарной установки имеют место явления и эффекты следующего порядка. Водяной пар подается в аппарат через регулятор, в котором он подвергается дросселированию. Далее водяной пар, накапливаясь в греющей камере, охлаждается до температуры конденсации. Конденсация пара сопровождается образованием пленки конденсата в наружных стенках кипятильных труб аппарата. Явление передачи тепла греющего пара через пленку конденсата к стенке аппарата происходит благодаря теплопроводности. Передача тепла от стенки к продукту можно характеризовать теплопроводностью, а последнего к концентрированному раствору -теплоотдачей. В дальнейшем (за счет поглощения тепла, передаваемого водяным паром) раствор сначала нагревается, затем начинает кипеть. В результате испарения воды из кипящей пульпы сахаросодержащих масс наблюдается образование смеси паров воды раствора; концентрация обрабатываемого раствора повышается.
Сахаросодержащая масса в аппарате имеют место процессы следующего порядка. Слабый раствор с концентрацией a0, температурой t0 и расходом G1 поступает через регулирующий орган в пространство аппарата. Затем пульпа сахаросодержащих масс, полностью перемешивается с помощью перемешивающего устройства. При этом предотвращается появления загара. Концентрация достигает значения a2 при температуре кипения t2 и остаточном давлении в ступени P2.
Таким образом, процесс выпаривания фугата сахаросодержащих масс сопровождается следующими явлениями и эффектами в аппарате:
по линии движения тепловой энергии греющего водяного пара: дросселирование пара в регуляторе → накопление пара в греющей камере → охлаждение пара до температуры ее конденсации → конденсация пара с образованием пленки → передача тепла посредством теплопроводности через пленку конденсата → передача тепла от пленки через стенки аппарата теплопроводности → концентрирование фугата сахаросодержащих масс в аппарате.
Математическая модель статики и динамики процесса концентрирования пищевых растворов в выпарных установок получена и исследована авторами работ [А].
Она включает:
- математическое описание процесса регулирования расхода греющего пара посредством исполнительного механизма — регулирующего клапана, установленного на линии греющего пара, с использованием для этого степени открытия клапана к и разности давлений в паропроводе P1 и в греющей камере P2;

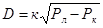 (1)
(1)
В данном случае коэффициент к характеризует проходное сечение сужающего устройства (регулирующего органа) и показателей пара (плотность, коэффициент сжимаемости и т. д.).
- математическое описание процесса конденсации пара в греющей камере, в виде:
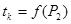 (2)
(2)
К теплообмену при идеальном смешении можно отнести элементарные процессы аппаратов, где температуры жидкости по всему объему будут близки. Процесс описывается математической моделью с сосредоточенными параметрами. Из уравнения теплового баланса:
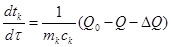 (2)
(2)
Количество теплоты при накопления пара:
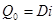 (3)
(3)
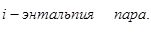
Количество теплоты при приходе пара:
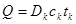 (4)
(4)
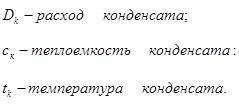
Количество теплоты при расходе конденсата:
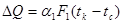 (5)
(5)
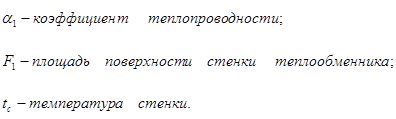
Плотность и температура конденсации пара зависят от давления пара в греющей камере.
Температура конденсации водяного пара обычно имеет нелинейную зависимость
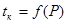 (6)
(6)
В условиях работы теплообменных аппаратов в пищевой промышленности температуру конденсации водяного пара можно определить по уравнению
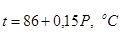 (7)
(7)
где Р — давление в МПа.
В больших пределах изменения давления tk можно аппроксимировать логарифмической зависимостью.
Таким образом, процесс в паровом пространстве, можно представить следующим в виде системы уравнений:
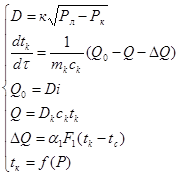 (8)
(8)
Как видно, описание динамики процесса конденсации, состоящее из двух описаний апериодических звеньев, указывает на очень маленькое время переходного процесса. Поэтому в исследование динамики процесса аппаратов этот процесс можно описать моделью усилительного звена и включить в математическую модель более инерционных звеньев.
Для получения подтверждения достоверности теоретических выкладок при исследование процесса проведены компьютерные исследования с использование программы «MATLAB» выше приведенной моделью (рис.2).
Скорость накопления тепла стенки (т. е. изменение тепла стенки) зависит от разности притока и расхода тепла к стенке (уравнение теплового баланса), т. е.
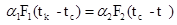 (9)
(9)
где a2 — коэффициент теплопередачи от стенки к сырье; F2 — поверхность выпарного аппарата, t, tk, tc- температуры сырья, конденсата и стенки.
Парожидкостное пространство выпарного аппарата образует внутренняя часть аппарата, в котором происходит сложный процесс выпарки сырья, характеризуемый непрерывным распределением его параметров (концентрации и температуры) по объему выпарного аппарата.
Структуру потоков смеси полупродукта в самом аппарате можно описать моделью идеального смешивание. В соответствии с принятыми предпосылками движение парожидкостной смеси, а аппарате периодическим перемешиваниям, потому что выпарка сырья сопровождается с перемешиванием. В этом случае математическое описание процесса выпарки сырья в парожидкостном пространстве описывается дифференциальным уравнением в частных производных, конкретный вид которого имеет следующий:
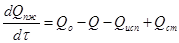 (10)
(10)
Здесь
Qпж — количество теплоты парожидкостного пространства 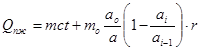 (11)
(11)
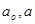 - начальные концентрации сырья и выпаренного продукта;
- начальные концентрации сырья и выпаренного продукта;
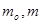 — масса сырья и выпаренного продукта;
— масса сырья и выпаренного продукта;
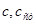 - теплоемкость сырья и стенки аппарата;
- теплоемкость сырья и стенки аппарата;
Qo — количество теплоты сырье 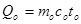 (12)
(12)
Q — количество теплоты выпаренного продукта 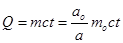 (13)
(13)
Qисп — количество теплоты испаренной воды 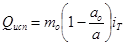 (14)
(14)
Qст — количество теплоты стенки аппарата 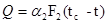 (15)
(15)
Изменения количество теплоты по времени
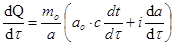 (16)
(16)
Здесь 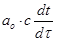 - изменения температуры по времени сырья;
- изменения температуры по времени сырья;
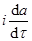 - изменения температуры по времени выпаренной воды.
- изменения температуры по времени выпаренной воды.
Объединив уравнения (10–16) в единую систему уравнений, получим математическую модель для процесса, протекающего в парожидкостном пространстве выпарного аппарата:
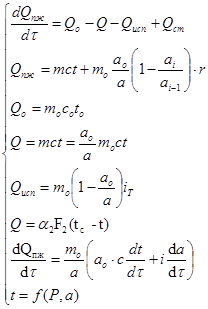 (17)
(17)
Математическое описание (17) характеризует нестационарное изменение концентрации и температуры парожидкостной смеси по объему аппарата и по времени при воздействии возмущения. Модель (17) представляет интерес для исследования динамики процесса, протекающего в парожидкостном пространстве выпарного аппарата.
На схеме.1 приставлена обобщенная компьютерная модель процесса выпарки сахаросодержащих масс с применением программы MATLAB (MATrix LABoratory — матричная лаборатория).
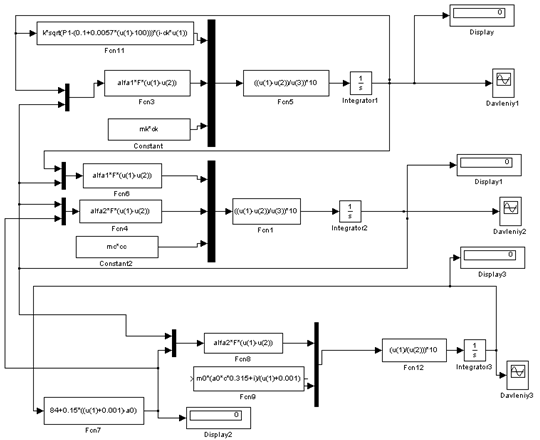
Рис. 1. Обобщенная компьютерная модель процесса выпарки сахаросодержащих масс
Результаты компьютерного моделирования процесса выпаривания приставлено на рис.2.
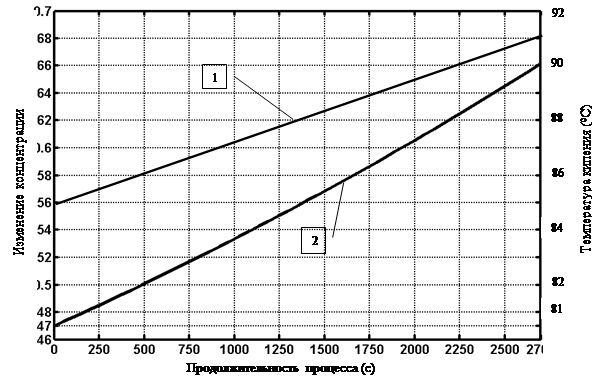
Рис. 2. Изменения концентрации сахаросодержащих масс процессе выпаривание
Таким образом, в результате исследования на компьютерной модели исследуемого процесса, выявлены конкретные технологические режимы проведения и определены конструктивные параметры выпарной установки. Это позволило совершенствовать организацию процесса выпаривания сахаросодержащих продуктов.
Составляя математическую модель процесса выпарки был проведен подробный анализ этого процесса. В результате исследования на компьютерной модели исследуемого процесса, выявлены конкретные технологические режимы проведения и определены конструктивные параметры выпарной установки, которое позволило совершенствовать организацию процесса выпаривания.
Литература:
1. Асмаев М. П., Корнилов Ю. Г. Моделирование процессов пищевых процессов. — М.: Легкая и пищевая промушленность, 1992. — 176 с.
2. Остапчук Н. В. Основы математического моделирования процессов пищевых производств. — Киев: Выща школа, 1991. — 367 с.
3. Кавецкий Г. Д., Васильев Б. В. Процессы и аппараты пищевой технологии. Учебник для группы специальностей “Технология продуктов питания” высших учебных заведений. — 2-е изд., перераб. и доп. — М.: Колос, 1999. — 551 с.
4. Ахметов К. А., Исмаилов М. А. Математическое моделирование и управление технологическими процессами биохимического производства.-Ташкент: Фан, 1993. — 95 с.
5. Патент №.IAP 03289. Способ приготовления повидло. Ш.Атаханов, Р.Хожиев, Х.Каноатов, А.Артиков.







