Использование дискретных моделей для исследования резонанса в сплошных средах

К исследованию резонансных явлений в механических системах и деформируемых средах применяются как дискретные, так и непрерывные модели. Простейшей дискретной моделью является линейная решетка Браве – цепочка частиц (материальных точек), соединенных последовательно пружинами равной жесткости. Масса частиц или одинакова во всей цепочке (моноатомная цепочка), или принимает одно из двух возможных значений (двухатомная цепочка). Волновые процессы в решетках Браве, в частности, резонансы, вызванные внешними периодическими воздействиями, изучались в линейном [1, 2] и нелинейном [3, 4] приближениях. Моделированию волн в двумерных решетках (прямоугольных и треугольных) посвящены работы [5, 6].

Простейшую непрерывную модель резонансной системы описывает одномерное волновое уравнение, получаемое с помощью предельного перехода в решетке Браве при стремлении к бесконечности числа частиц, причем предполагается конечность плотности и скорости упругих волн. Резонансные решения волнового уравнения для различных вариантов нелинейности получены в работах [7, 8]. В [9] приведены результаты исследования модельного одномерного уравнения для описания резонанса. Пространственные непрерывные модели структурно неоднородных сред, так называемых обобщенных континуумов, строятся с помощью метода гомогенизации [10, 11], позволяющего определить феноменологические параметры и функции состояния в определяющих уравнениях по заданным характеристикам дискретных систем. Среди моделей обобщенных континуумов исключительную роль играет модель Коссера, учитывающая вращательные степени свободы частиц микроструктуры среды. Анализу волновых процессов на основе уравнений континуума Коссера посвящены работы [12, 13]. В [14] показано, что с помощью уравнений ортотропного моментного континуума можно приближенно описать процессы распространения волн вращательного движения в блочных средах из упругих блоков, взаимодействующих через тонкие податливые прослойки.

Общие вопросы теории колебаний и резонансных явлений рассмотрены в монографиях [15–17]. Прикладные задачи о резонансном возмущении механических и физических систем исследовались многими авторами. В [18] демонстрируются возможности резонансного метода разрушения ледяного покрова с помощью изгибно-гравитационных поверхностных волн [19].

Общая постановка

Процесс распространения упругих волн бесконечно малой амплитуды в дискретных механических системах можно описать с помощью системы дифференциальных уравнений

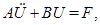                                                                                                           (1)

где 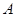 – симметричная положительно определенная матрица обобщенных масс;  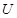– вектор обобщенных координат;  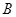– симметричная неотрицательно определенная матрица;  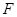– вектор внешних сил.

Для системы (1) верно уравнение 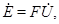 характеризующее изменение полной энергии: 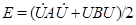. В случае, если вектор внешних сил зависит от времени периодически с частотой  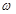(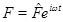), то периодическим будет и вектор обобщенных координат  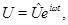при этом  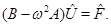Исключением являются только резонансные частоты, для которых нарушается условие периодичности  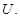Квадраты частот  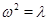являются корнями характеристического уравнения 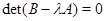. Поскольку матрицы  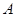и 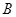 симметричные и знакоопределенные, корни данного уравнения действительные, а их число с учетом кратности равно размерности системы (1). Корням отвечают линейно независимые собственные векторы, каждый из которых является решением однородной системы .

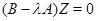Для нерезонансных частот 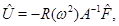 где 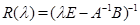 – резольвента,  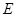– единичная матрица. Для исследования поведения системы в окрестности собственных частот используется спектральный портрет матрицы  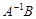[20]. С помощью спектрального портрета можно визуально отделить резонансные частоты и отследить изменение вектора  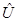в их окрестности.

Исследованы случаи продольных и вращательно-поперечных колебаний. В обоих случаях рассмотрена линейная дискретная цепочка из 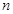 материальных точек массы  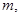соединенных между собой пружинами жесткости  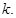Расстояние между материальными точками равно  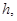длина цепочки в целом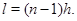

Продольные колебания

В данном случае к массам цепочки в продольном направлении приложены возмущающие силы 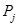, в результате которых массы получают перемещения 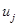, зависящие от времени (рис. 1).

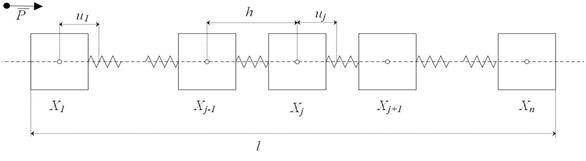
Рис. 1. Схема продольных колебаний цепочки

Уравнения движения в форме Лагранжа принимают вид

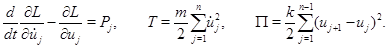
Здесь 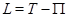 – функция действия,  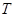– кинетическая энергия,  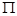– потенциальная энергия цепочки. Данные уравнения приводятся к системе (1), причем матрицы  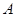и 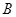 – якобиевы: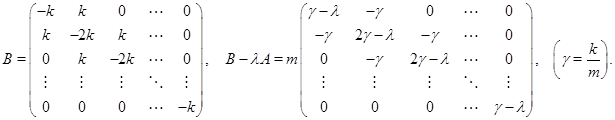    

Соответствующее характеристическое уравнение решается в явном виде [21]. Для этого строятся собственные векторы с компонентами 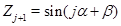, которые выражаются через параметры  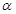и 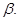 Система уравнений для собственных векторов автоматически выполняется, если

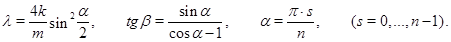
            Показано, что при увеличении числа элементов в линейной цепочке резонансные частоты стремятся к собственным частотам продольных колебаний однородного упругого стержня с граничными условиями, соответствующими способу закрепления концов цепочки [22, 23].

Для примера на рис. 2 изображен спектральный портрет матрицы дискретной цепочки для 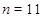 на плоскости действительных и мнимых осей  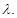В окрестности каждой из них амплитуды колебаний растут в равной степени по мере приближения к соответствующей резонансной частоте. Исключениями являются пятна, находящиеся на границах диапазона. Спектральный портрет для системы большего порядка качественно не меняется.

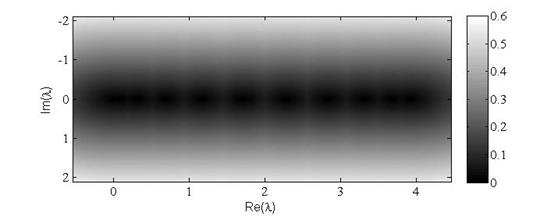
Рис. 2. Спектральный портрет матрицы A,n=11

Вращательно-поперечные колебания

Пусть на элементы цепочки действуют поперечные силы 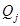 и вращательные моменты 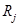, в результате чего элементы поворачиваются на малые углы  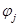и получают в поперечном направлении малые перемещения  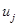(рис.3).

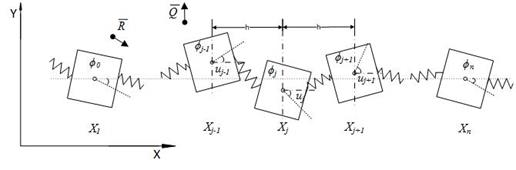
Рис. 3. Схема вращательно-поперечных колебаний цепочки

Предположим, что концы цепочки закреплены по перемещениям и свободны по вращениям, поставив граничные условия в виде

                                           (2)

после введения в цепочку двух дополнительных элементов с индексам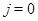и  и .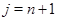

Деформированное состояние цепочки описывается величинами

            ,

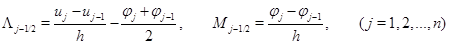первая из которых характеризует деформацию сдвига, а вторая – кривизну. Выбор характеристик деформирования в таком виде объясняется тем, что обе они тождественно равны нулю при абсолютно жестком движении, когда вся цепочка с освобожденными концами поворачивается на произвольный бесконечно малый угол.

Упругое сопротивление пружин в цепочке моделируется с помощью уравнений 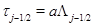, , 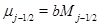связывающих перерезывающие силы  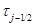и вращательные моменты  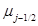с деформациями и кривизнами. Уравнения Лагранжа принимают следующий вид:

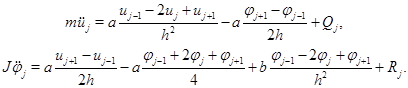                                    (3)

Уравнения (3) также можно представить в виде системы (1) с симметричными и знакоопределенными матрицами. Подстановка в однородные уравнения выражений

     ,

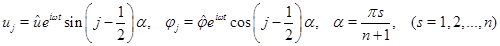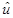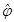которые автоматически удовлетворяют граничным условиям, приводит к системе линейных уравнений для амплитуд  и . Условие равенства нулю определителя системы, представляющее собой условие существования нетривиальных решений, позволяет получить биквадратное уравнение для определения собственных частот цепочки:

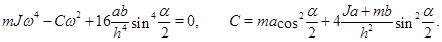
Отсюда

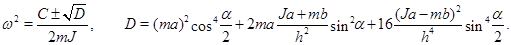          (4)

Собственные частоты при естественных ограничениях на параметры цепочки (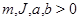) всегда действительные и различные для разных  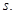Если номер  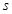зафиксировать, то при заданной длине цепочки  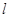существуют конечные пределы

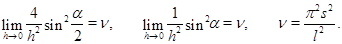
С помощью этих пределов коэффициенты формулы (4) для квадрата частоты бесконечной цепочки упрощаются:

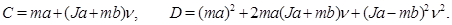
Устремляя теперь 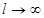, то есть 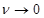, можно установить, что  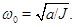Это единственная собственная частота в бесконечной цепочке бесконечной длины, которая связана с вращательным движением элементов. Других резонансных частот нет.

На рис. 4 изображен матричный портрет для дискретной цепочки из 9 элементов. По размеру пятен на этом рисунке можно судить о том, что при приближении к частоте 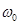 амплитуды колебаний нарастают примерно в такой же степени, как и при приближении к остальным резонансным частотам.

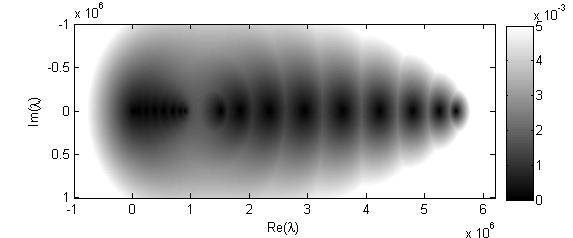
Рис. 4. Спектральный портрет матрицы,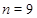

Уравнения (3) в пределе для бесконечной цепочки длины 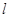 переходят в одномерные дифференциальные уравнения континуума Коссера:

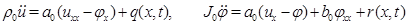                                       (5)

с граничными условиями 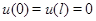, 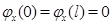. Коэффициенты уравнений пересчитываются через механические параметры дискретной модели из соображений сохранения полной массы и суммарного момента инерции, а собственные частоты континуума вычисляются по формулам, которые могут быть получены предельным переходом в формулах для частот собственных колебаний конечной цепочки. Резонансные свойства континуума Коссера на основе моделей пространственного напряженно-деформированного состояния изучались в монографии [24]. Было установлено, что в моментной среде существует резонансная частота, связанная с вращательным движением частиц, не зависящая от размеров области и от типа граничных условий на ее границе.

Таким образом, показано, что при поперечных и вращательных колебаниях дискретной цепочки возникает целая система резонансных частот, зависящих от числа элементов и длины цепочки. Наряду с ней существует единственная резонансная частота вращательного движения, которая определяется только значениями механических параметров модели.

Работа выполнена при финансовой поддержке РФФИ (код проекта 14-01-00130).

Литература:

1.      Belbasi S., Foulaadvand M.E., Yong S.J. Anti-Resonance in a One-Dimensional Chain of Driven Coupled Oscillators // American Journal of Physics, 2014. – V. 82, No. 32. – P. 32–38.  http://dx.doi.org/10.1119/1.4827277

2.      Grundmann M. The Physics of Semiconductors: An Introduction Including Nanophysics and Applications // Springer Science & Business Media, 2011. – 901 p.

3.      Narisetti Raj K., Wave propagation in nonlinear periodic structures, dissertation (Georgia Institute of Technology), 2010.

4.      Filip A.-M., Venakides S. Existence and Modulation of Travelling Waves in Particle Chains // Communications on Pure and Applied Mathematics, 1999. – V. 52. Iss. 6. – P. 693–735. http://dx.doi.org/10.1002/(SICI)1097-0312(199906)52:6<693::AID-CPA2>3.0.CO;2-9 

5.      Ayzenberg-Stepanenko M.V., Slepyan L.I. Resonant-Frequency Primitive Waveforms and Star Waves in Lattices // Journal of Sound and Vibration, 2008. – V. 313. Iss. 3-5. – P. 812–821. http://dx.doi.org/10.1016/j.jsv.2007.11.047

6.      Feckan M., Rothos V.M. Travelling Waves in Hamiltonian Systems on 2d Lattices with Nearest Neighbor Interactions // Institute of Physics Publishing, Nonlinearity, 2007. – V. 20, No. 2. – P. 319–341. http://dx.doi.org/10.1088/0951-7715/20/2/005

7.      Manevich A.I., Manevich L.I. The mechanics of nonlinear systems with internal resonances, ISBN: 1-86094-510-4, Imperial College Press, London. – 276 p.

8.      Collins W.D. Forced Oscillations of Systems Governed by One-Dimensional non-Linear Wave Equations // Quart. Journ. Mech. And Applied Math, 1971. – V. 24, No. 2. – P. 129–153. http://dx.doi.org/ 10.1093/qjmam/24.2.129

9.      Bretherton F.P. Resonant Interactions between Waves. The Case of Discrete Oscillations // J. Fluid Mech, 1964. – V. 20, No. 3. – P. 457–479. http://dx.doi.org/10.1017/ S0022112064001355

10.  Boutin C., Hans S. Homogenization of Periodic Discrete Medium: Application to Dynamics of Framed Structures // Comput. Geotech, 2003. – V. 30, No. 4. – P. 303–320. http://dx.doi.org/10.1016/S0266-352X(03)00005-3

11.  Tollenaere H., Caillerie D. Continuous Modeling of Lattice Structures by Homogenization // Adv. Eng. Softw, 1998. – V. 29. Iss. 7-9. – P. 699–705. http://dx.doi.org/10.1016/S0965-9978(98)00034-9

12.  Sadovskaya O.V., Sadovskii V.M. Analysis of Rotational Motion of Material Microstructure Particles by Equations of the Cosserat Elasticity Theory // Acoust. Phys, 2010. – V. 56, No. 6. – P. 942–950. http://dx.doi.org/10.1134/S1063771010060199

13.  Sadovskii V.M., Sadovskaya O.V., Varygina M.P. Numerical Solution of Dynamic Problems in Couple-Stressed Continuum on Multiprocessor Computer Systems // Int. J. Numer. Anal. Model. Ser. B, 2011. – V. 2, No. 2–3. – P. 215–230.

14.  Sadovskii V.M., Sadovskaya O.V. Modeling of Elastic Waves in a Blocky Medium Based on Equations of the Cosserat Continuum // Wave Motion, 2015. – V. 52. – P. 138–150.  http://dx.doi.org/10.1016/j.wavemoti.2014.09.008

15.  Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. – М.: Физматлит, 1963. – 410 с.

16.  Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. – М.: Наука, 1988. – 328 с.

17.  Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры: научное издание. – М.: Физматлит, 2003. – 492 с.

18.  Козин В.М. Резонансный метод разрушения ледяного покрова. Изобретения и эксперименты. – М.: Академия естествознания, 2007. – ISBN: 978-5-91327-017-7. – 355 с.

19.  Milewski P.A., Wanf Z. Three-Dimensional Flexural-Gravity Waves // Studies in Applied Mathematics, 2013. – V. 131. Iss. 2. – P. 135–148.  http://dx.doi.org/10.111/ sapm.12005

20.  Годунов С.К. Современные аспекты линейной алгебры. – Новосибирск: Научная книга, 1997. – 284 с.

21.  Воеводин В.В., Кузнецов Ю.А Матрицы и вычисления. – М.: ФИЗМАТЛИТ, 1984. – 320 с.

22.  Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. – М.: Наука, Гл. ред. ФИЗМАТЛИТ, 1986. – 560 с.

23.  Биргер И.А., Пановко Я.Г. Прочность. Устойчивость. Колебания. – Справочник в 3 томах. – Том 3. – М.: Машиностроение, 1968. – 567 с.

24.  Sadovskaya O.V., Sadovskii V.M. Mathematical Modeling in Mechanics of Granular Materials. Ser.: Advanced Structured Materials, V. 21. Springer, Heidelberg – New York – Dordrecht – London, 2012. – 390 p. http://dx.doi.org/10.1007/978-3-642-29053-4, ISBN: 978-3-642-29052-7.