Введение
При численном решении жестких задач большой размерности возникает необходимость использования алгоритмов на основе явных методов [1–3]. Методы интегрирования на основе неявных или полуявных численных схем используют обращение матрицы Якоби [1]. В данном случае это отдельная трудоемкая задача. В такой ситуации предпочтительнее применять алгоритмы на основе явных формул, если жесткость задачи позволяет за разумное время получить приближение к решению. Здесь с применением предложенного в [3] способа оценки максимального собственного числа матрицы Якоби построено неравенство для контроля устойчивости метода Ческино второго порядка точности [4]. На основе стадий численной формулы Ческино разработан метод первого порядка точности с расширенным до 32 интервалом устойчивости. Сформулирован алгоритм интегрирования переменного порядка и шага. Приведены результаты расчетов.
Метод Ческино
Рассматривается задача Коши
, 
, 
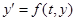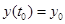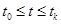, (1)
где 
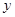и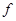 
– 
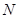-мерные вещественные вектор-функции; 
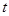– независимая переменная, которая изменяется на заданном интервале 
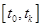. Для решения (1) будем использовать явные формулы типа Рунге-Кутты
,
, 
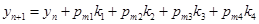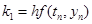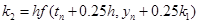, (2)
, 
,
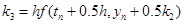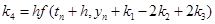где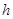 
– шаг интегрирования; 
, 
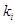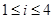– стадии метода; 
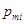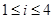, – числовые коэффициенты; 
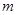– порядок точности метода. При коэффициентах
, 
, 
, 
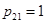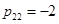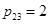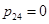(3)
схема (2), (3) имеет второй порядок точности [4].
Схема (2) с коэффициентами
, 
, 
, 
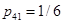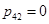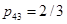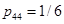
имеет четвертый порядок. Тогда для контроля точности схемы второго порядка можно использовать оценку ошибки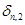 
вида
.
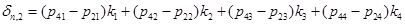В результате для контроля точности вычислений применяется неравенство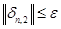 
, где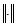 
– есть некоторая норма в 
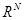, а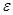 
– требуемая точность расчетов. Имеет место соотношение 
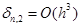. Тогда шаг 
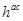по точности будем выбирать по формуле 
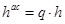, где значение 
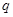находится из уравнения 
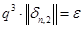. Если 
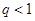, то происходит повторное вычисление решения (возврат) с шагом 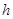, равным 
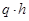. В противном случае вычисляется приближенное решение, а прогнозируемый шаг 
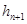вычисляется по формуле 
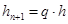. Неравенство 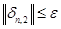хорошо зарекомендовало себя при решении многих задач и далее будет использоваться здесь. Ниже алгоритм переменного шага на основе схемы (2), (3) с неравенством для контроля точности 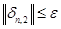назовем 
.
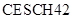Контроль устойчивости
Построим неравенство для контроля устойчивости схемы (2). Для этого применим (2) для решения линейной задачи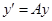 
с постоянной матрицей 
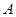. Первые три стади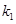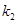и 
, 
и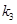 
применительно к данной задаче имеют вид
, 
, 
,
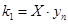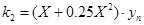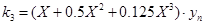где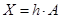 
. Нетрудно видеть, что имеют место соотношения
, 
.
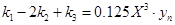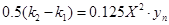Оценку максимального собственного числа матрицы Якоби системы (1) можно вычислить степенным методом [3]. Введем обозначение
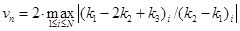. (4)
Для контроля устойчивости метода Ческино можно применять неравенство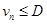 
, где число 
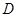ограничивает интервал устойчивости.
Устойчивость методов типа Рунге-Кутта обычно исследуется на скалярном тестовом уравнении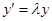 
, где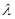 
есть произвольное комплексное число, 
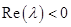. Смысл 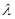– некоторое собственное число матрицы Якоби системы (1). Применяя (2), (3) для решения 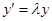, получим, что функция устойчивости 
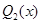метода второго порядка имеет вид 
, 
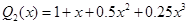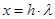, а функция устойчивости 
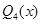метода четвертого порядка – 
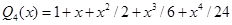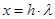, . Интервал устойчивости метода второго порядка равен двум (рис. 1), а схемы четвертого порядка приблизительно равен 2.8 (рис. 2). Поэтому в неравенстве 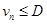положим 
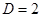. Учитывая, что 
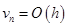, шаг 
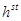по устойчивости можно выбирать по формуле 
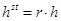, где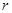 
вычисляется из равенства 
.
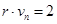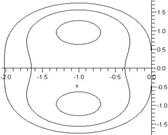
Рис. 1. Область устойчивости метода второго порядка
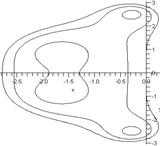
Рис. 2. Область устойчивости метода четвертого порядка
Оценка (4) является грубой, потому что вовсе не обязательно максимальное собственное число сильно отделено от остальных, в степенном методе применяется мало итераций и дополнительные искажения вносит нелинейность задачи (1). Поэтому контроль устойчивости используется как ограничитель на размер шага интегрирования. В результате прогнозируемый шаг вычисляется по формуле
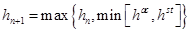, (5)
где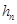 
есть последний успешный шаг интегрирования. Отметим, что формула (5) применяется для прогноза величины шага интегрирования 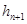после успешного вычисления решения с предыдущим шагом 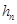, и поэтому фактически не приводит к увеличению вычислительных затрат. Если шаг по устойчивости меньше последнего успешного, то он уменьшен не будет, потому что причиной этого может быть грубость оценки максимального собственного числа. Однако шаг не будет и увеличен, потому что не исключена возможность неустойчивости численной схемы. Если шаг по устойчивости должен быть уменьшен, то в качестве следующего шага будет применяться последний успешный шаг 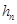. В результате для выбора шага и предлагается формула (5), которая позволяет стабилизировать поведение шага на участке установления решения, где определяющую роль играет устойчивость. Именно наличие данного участка существенно ограничивает возможности применения явных методов для решения жестких задач.
В дальнейшем алгоритм переменного шага с дополнительным контролем устойчивости численной схемы будем называть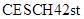 
. Данный алгоритм основан на численной формуле невысокого (второго) порядка точности, и поэтому он ориентирован на решение нежестких задач с небольшой точностью расчетов (порядка 1% и ниже), а также задач умеренной жесткости. Из результатов расчетов алгоритмом 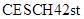следует, что фактическая точность вычислений на участке установления значительно выше задаваемой точности. Это естественно, потому что на данном участке старые ошибки подавляются за счет контроля устойчивости, а новые невелики за счет малости производных решения. В такой ситуации эффективнее проводить расчеты по методу низкого порядка с более широкой областью устойчивости.
Метод первого порядка
На основе стадий численной схемы (2) построим метод первого порядка точности вида
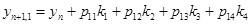(6)
с более широкой областью устойчивости. Для этого применим (6) для решения тестового уравнения 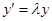. Получим 
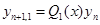, где ,
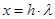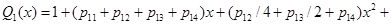
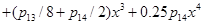. (7)
Требование первого порядка точности численной формулы (7) означает выполнение соотношения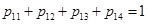 
. Остальные коэффициенты 
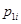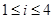, применим для расширения области устойчивости. Условие устойчивости схемы (6) имеет вид 
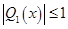. Для построения метода с максимальным интервалом устойчивости рассмотрим многочлен Чебышева вида 
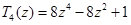. Известно, что полином 
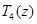наименее отклоняется от нуля для 
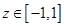. Проведем замену переменных 
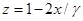, при этом отрезок 
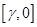отображается на промежуток 
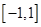. В результате многочлен 
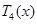записывается в виде
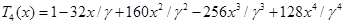. (8)
Нетрудно показать [3], что для полинома 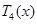неравенство 
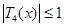выполнятся на максимальном интервале , 
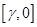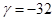(рис. 3). Сравнивая соотношения (7) и (8) при 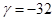, получим коэффициенты 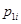, 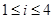метода (2) первого порядка точности с максимальным интервалом устойчивости, то есть
, 
,
,
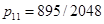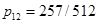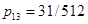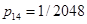. (9)
Область устойчивости метода первого порядка (6), (9) по вещественной оси в 16 раз шире области устойчивости численной схемы (2), (3). Вычислительные затраты в методах первого и второго порядков совпадают. Поэтому для задач, в которых шаг ограничен в основном по устойчивости, предполагаемое теоретическое повышение эффективности в 16 раз.
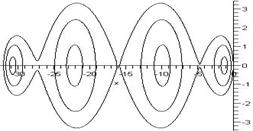
Рис. 3. Область устойчивости метода первого порядка
В неравенстве для контроля точности будем применять оценку ошибки вида
.
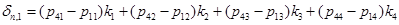Для контроля точности численной формулы (6), (9) можно применять неравенство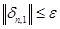 
. Так как интервал устойчивости численной схемы (6), (9) ограничен числом 32, то для ее контроля устойчивости можно применять неравенство 
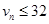, где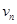 
определяется по формуле (4).
Метод первого порядка с расширенной областью устойчивости эффективен на участках установления, где шаг ограничен по устойчивости. На переходных участках эффективнее будет метод (2), (3). Повышения эффективности можно достичь за счет применения каждого метода на том участке, где он наиболее эффективен. В качестве критерия переключения с метода на метод можно использовать неравенство для контроля устойчивости. При расчетах по методу (2), (3) переход на численную схему (6), (9) осуществляется при нарушении неравенства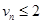 
. При расчетах методом первого порядка обратный переход происходит в случае выполнения 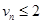. Вычисления методом первого порядка сопровождаются дополнительным (наряду с точностью) контролем неравенства 
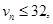а шаг выбирается по формуле типа (5). Ниже алгоритм переменного порядка и шага будем называть 
.
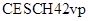Химическая кинетика
Численное исследование построенных алгоритмов интегрирования проводилось на дифференциальных уравнениях химической кинетики. Кинетическая схема химической реакции состоит из элементарных стадий вида
,
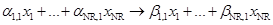… … … (10)
,
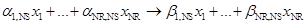где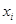 
, 
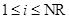– реагенты; 
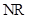и 
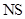– соответственно, число реагентов и число стадий в реакци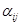и; 
и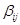 
, , 
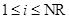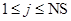– стехиометрические коэффициенты. Для каждой элементарной реакции заданы константы скоростей стадии 
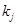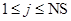, . Процессу (10) в рамках сосредоточенной модели изотермического реактора постоянного объема соответствует система обыкновенных дифференциальных уравнений
, 
.
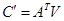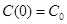Здесь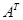 
– стехиометрическая матрица; 
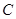и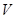 
– вектор концентраций реагентов и скоростей стадий, соответственно. В случае протекания реакции в неизотермических условиях к данной системе добавляется уравнение теплового баланса
,
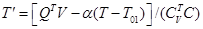где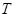 
– температура смеси в реакторе; 
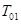– температура стенок реактора; 
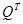– вектор удельных теплот стадий; 
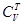– вектор теплоемкостей реагентов;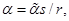 
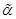– коэффициент теплоотдач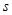и; 
и 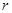– площадь поверхности и объем реактора, соответственно. Верхний индекс 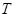у векторов 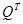и 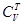означает транспонирование. Теплоемкости реагентов и коэффициент теплоотдачи могут быть функциями концентраций реагентов 
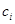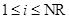, , а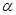 
может еще зависеть от температуры.
Если реакция протекает в изотермическом реакторе постоянного объема с обменом вещества (открытая система, реактор идеального смешения), система дифференциальных уравнений записывается в виде
, .
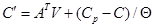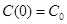где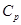 
– вектор концентраций реагентов на входе в реактор; 
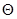– время пребывания смеси в реакторе;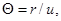 
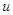– объемная скорость течения смеси через реактор. В неизотермических условиях система дополняется уравнением теплового баланса
,
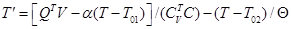где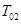 
– температура смеси на входе в реактор. Температура реагирующей смеси может задаваться в виде функции времени t и концентраций реагентов , .
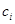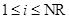Если стадия обратима, то под скоростью стадии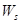 
принимается разность скоростей прямого 
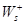и обратного 
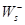процессов, то есть 
, 
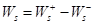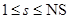. Если в стадии участвует третья частица, то скорость 
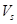вычисляется по формулам [5]
, 
, ,
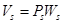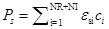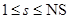где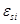 
, , 
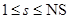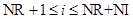– эффективности третьих частиц; 
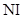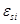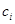– число инертных веществ; и – эффективности и концентрации инертных веществ, соответственно. Значения компонент вектора 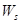определяются из схемы химической реакции (10) по соотношениям
, 
,
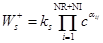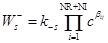где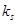 
и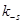 
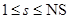, – константы скоростей прямой и обратной стадий, соответственно. Константы скоростей стадий вычисляются по формулам
,
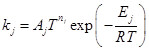где 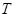– температура смеси в реакторе; 
, 
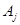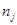и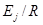 
– заданные постоянные. Заметим, что, вообще говоря, константы скоростей в случае неизотермического реактора постоянными не являются – они зависят от температуры. Однако исторически сначала рассматривался изотермический реактор, и 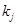, 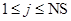в настоящее время по-прежнему называют константами.
Стехиометрическая матрица 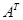с элементами 
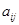формируется из кинетической схемы (10) по следующему правилу. Номер стадии совпадает с номером столбца, а номер реагента с номером строки матрицы 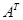. Если 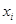выступает как исходный реагент, то 
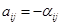, если 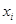– продукт, то 
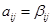. Если 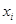является одновременно исходным реагентом и продуктом, то 
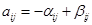. Обычно в элементарной стадии участвует небольшое количество реагентов, то есть стехиометрическая матрица сильно разрежена.
Пиролиз этана
Запишем систему дифференциальных уравнений, описывающих пиролиз этана. Пиролиз этана в отсутствии кислорода описывается небольшой последовательностью стадий. Механизм пиролиза этана неоднократно обсуждался в литературе. Здесь принята схема реакции, предложенная и исследованная в [6]
, 
,
, 
, 
.
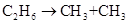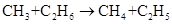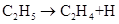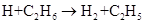Здесь константы скоростей стадий имеют вид:
, 
, 
, 
, 
.
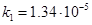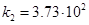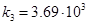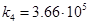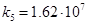Обозначим концентрации реагентов следующим образом:
, 
, 
, 
,
, 
, 
, 
.
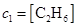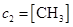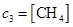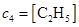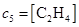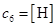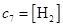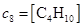Тогда соответствующая система состоит из 8 обыкновенных дифференциальных уравнений вида 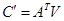, то есть
, 
,
, 
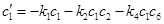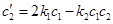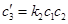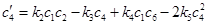, (11)
, 
, 
, 
.
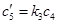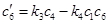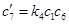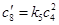Начальная концентрация этана 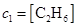равна 0.14, для остальных реагентов концентрации равны нулю.
Результаты расчетов
Расчеты осуществлялись с точностью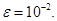 
Эффективность алгоритмов интегрирования оценивалась по числу вычислений правой части 
задачи (11) на интервале интегрирования. Численное решение осуществлялось на промежутке [0, 0.26]. Данная задача удовлетворяет ”классическому” определению жесткости. В начале интервала интегрирования наблюдается переходный участок (сотые доли секунды), а затем происходит медленное установление (рис. 4).
Сравнение эффективности построенных алгоритмов проводилось с известным методом Мерсона (
, [7]). Для обоих методов фактическая точность не хуже задаваемой точности. В случае применения явных методов для решения жестких задач шаг почти на всем промежутке интегрирования ограничен устойчивостью. В результате фактическая точность вычисления решения получается значительно выше задаваемой. На рис. 4 графики решений для метода Мерсона и построенного алгоритма 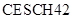практически совпадают. Алгоритму 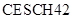без контроля устойчивости для нахождения решения потребовалось 
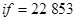, для алгоритма с контролем устойчивости 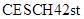имеет место 
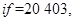для алгоритма переменного порядка и шага 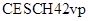затраты 
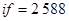, а для метода Мерсона 
.
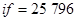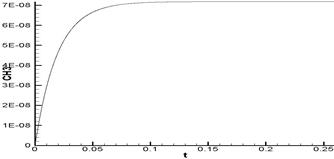
Рис. 4. Зависимость CH3 от времени
Заключение
Из результатов расчетов можно сделать следующие выводы. Во-первых, построенный алгоритм интегрирования второго порядка с контролем точности вычислений и устойчивости численной схемы, а также алгоритм переменного порядка и шага можно применять для решения достаточно жестких задач. Во-вторых, по вычислительным затратам алгоритм переменного порядка и шага эффективнее метода Мерсона почти в 10 раз. Это является следствием контроля устойчивости численной схемы и расчетов с переменным порядком. Представляется, что при достаточно большой размерности задачи (1) метод может конкурировать с неявными методами на задачах умеренной жесткости, потому что в нем не обращается матрица Якоби. 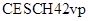При решении двенадцати тестовых задач [1] и десяти примеров [8] преимущество алгоритма выше.
Работа выполнена при финансовой поддержке РФФИ (проект 14-01-00047)
Литература:
1. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи: монография / Э. Хайрер, Г. Ваннер. – М.: Мир, 1999. – 685 c.
2. Хайрер Э. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: монография / Э. Хайрер, С. Нерсетт, Г. Ваннер. – М.: Мир, 1990. – 512 с.
3. Новиков Е.А. Явные методы для жестких систем: монография / Е.А. Новиков. – Новосибирск: Наука, 1997. – 197 с.
4. Ceschino F. Numerical solution of initial value problems: monograph / F. Ceschino, G. Kuntzman. – New Jersey: Prentice-Hall, Englewood Clis, 1966. – 347 p.
5. Новиков Е.А. Численное моделирование модифицированного орегонатора (2,1)-методом решения жестких задач / Е.А. Новиков // Вычислительные методы и программирование. – 2010. – Т. 11, № 2. – С. 123–130.
6. Kulich D.M. Mathematical simulation of the oxygen ethane reaction / D.M. Kulich and J.E. Taylor J. // Chem. Kinetic. – 1975. – Vol. 8. – P. 89–97.
7. Merson R.H. An operational methods for integration processes / R.H. Merson // Australia: Proc. of Symp. on Data Processing. – 1957. – P. 329–331.
8. Enright W.H. Comparing numerical methods for the solutions of systems of ODE’s, / W.H. Enright, T.E. Hull // BIT. – 1975. – No. 15. – P. 10–48.
