Цель данной статьи — представление некоторых методических особенностей реализации решения одной из широко известных и востребованных в различных научных областях задачи теории вероятностей — задачи нахождения вероятности попадания случайной величины в заданный интервал.
Ключевые слова: информационные технологии, информатизация образования, WolframAlpha, бакалавриат, бакалавр экономики, прикладная математическая подготовка, стохастика, вероятность, случайная величина.
Современную математику можно определить как науку об абстрактных структурах, выражающих количественные отношения объективной реальности (в том числе социально-экономической). Одновременно математизация теории — один из древнейших способов синтеза научных знаний. Именно процесс математизации экономической теории на основе абстрактности математических понятий (Рагнар Фриш, Ян Тинберген, Пол Самуэльсон, Джон Хикс, Кеннет Эрроу, Василий Леонтьев, Леонид Канторович, Джон Нэш, Райнхард Зелтен и др.) обеспечивает общность научно-методологических принципов. Синергетическое взаимодействие количественных и качественных, формальных и содержательных методов исследования экономических проблем и ситуаций составляет основу математизации научного знания в экономике. Следовательно, математическую подготовку бакалавра экономики следует рассматривать как системообразующую составляющую фундаментальной подготовки студента и элементом общей культуры. Методы теории вероятностей и математической статистики, об одном из которых пойдет речь в рамках статьи являются необходимым для экономистов инструментом работы с разнообразной экономической информацией.
Вероятностные и математико-статистические методы используются при изучении массовых совокупностей наблюдаемых явлений и обработке их результатов, в выявлении закономерностей случайных явлений. Теория вероятностей и математическая статистика имеет важное методологическое значение как в познавательном процессе, так и в выявлении общих закономерностей, выдвижении и исследовании гипотез, служит основной индуктивно-дедуктивных умозаключений. Образовательная область «Стохастика» (Теория вероятностей, Математическая статистика, Теория случайных процессов) в соответствии с требованиями мировых образовательных стандартов подготовки бакалавра экономики — обязательный элемент содержания фундаментальной и прикладной математической подготовки студентов. Разнообразные вероятностные задачи предоставляют широкие возможности для усиления прикладной экономической направленности обучения математике. При этом использование современных информационных технологии в учебном процессе способно обеспечить инструментальную основу для расширения перечня рассматриваемых проблем и ситуаций, с большей степенью адекватностью социально-экономической действительности современной России.
К настоящему времени база знаний и система вычислительных алгоритмов WolframAlpha стала неотъемлемым компонентом методики математической подготовки бакалавров, разрабатываемой и внедряемой авторами [3,4,5].
Отметим, что обозначенная выше задача в WolframAlpha решается достаточно просто, не вызывая затруднений у большинства студентов. Учитывая современную тенденцию прикладной направленности математической подготовки в высших учебных заведениях России, особую важность это приобретает при обучении математике студентов нематематических направлений подготовки (будущих экономистов, а также психологов, политологов, менеджеров, биологов, экологов и т. д.).
Вероятность попадания случайной величины X в заданный числовой интервал (a; b) с помощью математической символики записывается как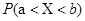 
. Величина вероятности зависит от того, какое распределение вероятностей имеет случайная величина. На этом важном факте следует акцентировать внимание студентов и только после этого переходить к построению соответствующего вычислительного процесса.
В большинстве пособий для высшей школы по курсу математики чаще всего подробно рассматривается вопрос о вычислении вероятности попадания в заданный интервал лишь для нормально распределенной случайной величины, а также для дискретных случайных величин, имеющих биномиальное распределение вероятностей [1,2]. Потенциал WolframAlpha в полной мере раскрывается при решении задач, в которых функция распределения имеет какое-либо иное распределение вероятностей. Как правило, большинство студентов о данном классе вероятностных задач имеет лишь отдаленное представление.
Однако при глубоком изучении управленческих, экономических, финансовых дисциплин возникает необходимость существенного расширения класса прикладных задач, требующих привлечение более «тонких» математических методов. Причем, здесь важно не ограничиться исключительно нормальным или биномиальным распределением вероятностей.
Переходим к основному техническому вопросу: каким образом определить вероятность попадания в заданный интервал для любой случайной величины? В WolframAlpha для этого следует ввести соответствующий запрос на вычисление вероятности, необходимо указать распределение случайной величины, а так же параметры распределения.
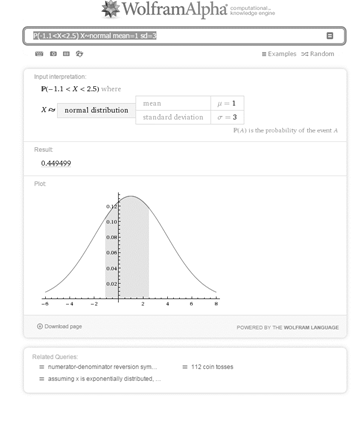
Рис. 1. Реализация поиска вероятности попадания непрерывной случайной величины в заданный интервал
Проиллюстрируем вышесказанное на примере. Для того, чтобы найти вероятность попадания непрерывной случайной величины X, имеющей нормальное распределение с параметрами (математическое ожидание)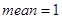 
и (средне-квадратическое отклонение) 
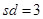в интервал 
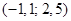используется соответствующий запрос:
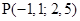: P(-1.1<X<2.5) X~normal mean=1 sd=3.
Анализируя рис. 1, отметим, что WolframAlpha позволяет не только представить числовой результат — значение искомой вероятности, равное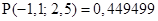 
, но также и его графическую интерпретацию для более глубокого представления ситуации и исследования содержательного смысла. На построенном графике плотности нормального распределения автоматически выделена фигура (криволинейная трапеция), площадь которой равна найденному значению вероятности 
.
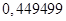Интересно, что этот факт соответствует известной формул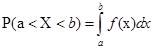е: 
, где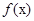 
— плотность вероятности нормального распределения). Другими словами, для непрерывных случайных величин тот же самый результат можно было бы получить путем непосредственного интегрирования.
Заключение.
1. Прикладная математическая подготовка бакалавра экономики в современных условиях приобретает не только педагогическое, но и социокультурное значение. Она призвана обеспечить готовность выпускников к осознанному использованию математических и инструментальных методов исследования широкого класса экономических проблем и ситуаций, оптимизации производственно — технологических процессов. Решающую роль уровень прикладной математической подготовки играет при решении профессиональных задач, принятии решений в условиях риска и неопределенности.
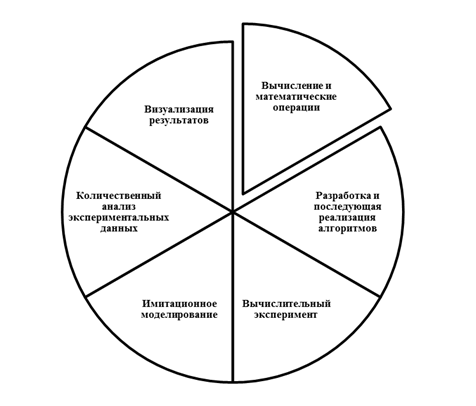
Рис. 2 Области применения WolframAlpha в учебном процессе
2. Целесообразное, дозированное и методически оправданное использование базы знаний WolframAlpha при работе с математическими моделями студентами бакалавриата (как на аудиторных занятиях, так и в процессе самостоятельной исследовательской работы) является условием более эффективного развития профессиональной компетентности студентов в соответствии с требованиями ФГОС 3+.
3. Разработанная и совершенствуемая авторами методика проведения практических занятий по прикладной математике, особенностью которой является интегрированное использование WolframAlphaи актуальных мировых информационных ресурсов, позволяет в большей мере сформировать готовность будущих экономистов к осознанному, активному и плодотворному использованию математических и инструментальных средств, методов в будущей профессиональной деятельности. В учебном пособии [6] доступно представлен широкий круг проблем и методов классического математического анализа, линейной алгебры, математического программирования, теории игр, теории вероятностей, математической статистики, теории случайных процессов и нечетких множеств. Наиболее востребованные области применения WolframAlpha, выделенные в процессе экспериментальной работы, представлены на рис. 2.
Литература:
1. Баврин И. И. Математика. Высшее профессиональное образование. Бакалавриат. М.: Академия, 2013–624 с.
2. Гусак А. А., Бричикова Е. А. Теория вероятностей. Справочное пособие к решению задач. Минск: ТетраСистемс, 2009–288 с.
3. Власов Д. А., Синчуков А. В. Новые технологии WolframAlpha при изучении количественных методов студентами бакалавриата. // Вестник Российского университета дружбы народов. Серия: Информатизация образования. 2013. № 4. С. 43–53.
4. Власов Д. А., Синчуков А. В. Стратегия развития методической системы математической подготовки бакалавров // Наука и школа. — 2012. — № 5. — С. 61–65.
5. Власов Д. А., Синчуков А. В. База знаний и набор вычислительных алгоритмов WolframAlpha при обучении студентов бакалаврита количественным методам. // Материалы Международной научной конференции ИНФОРМАТИЗАЦИЯ ОБРАЗОВАНИЯ — 2014 Информатизация образования 2014, Республика Беларусь, г. Минск, БГУ, БГПУ им. М. Танка
6. Власов Д. А., Синчуков А. В. Элементы высшей математики: базовый курс. Учебное пособие. М.: Типография «11 — й Формат», 2014. — 96 с.
