Упругие волны, распространяющихся в грунте от различных промышленных и транспортных источников, вредно влияют на сооружения, технологические процессы и на людей. Поэтому изучение действия этих волн на сооружения и разработка способов уменьшения вибраций до уровня требований санитарных норм имеют больше практическое значение.
Рассмотрим задачу о распространении колебаний в грунте, возникающих при движении железнодорожных поездов.
На основании экспериментальных исследований можно считать, что колебания грунта происходит во времени по гармоническому закону, задачу можно рассматривать в линейной постановке, так как амплитуда колебаний мала. Длина поезда, возбуждающего колебания грунта, составляет 300–500 метров, что, как правило, превышает длину обычных зданий. Следовательно, можно принять, что задача плоская и предположим, что колебания происходит по гармоническому закону [1].
Рассмотрим случай, когда закон деформирования подчиняется законам наследственной ползучести Больцмана-Вольтерра [2].
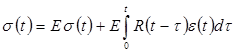(1)
или 
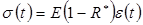(2)
где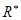 
- оператор релаксации.
Пусть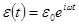 
, 
.
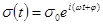Следовательно
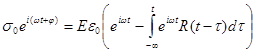. (3)
После преобразования, получим
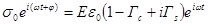(4)
, 
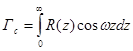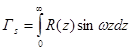
Обозначим
, 
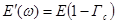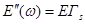
Тогда уравнении (1) принимает вид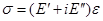 
.
Используется комбинированное экспоненциально-степенное ядро, предложенное А. Р. Ржаницыным [2]
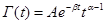(5)
Конкретные расчеты произведены при
А=1,373·10–2, β=1,3·10–7, α=0,2 — для грунта
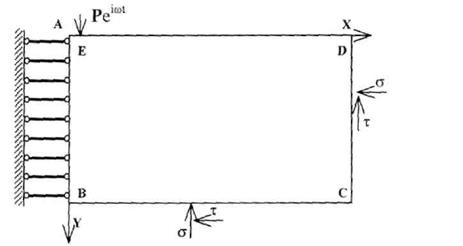
Рис. 1. Расчетная схема
На границе АВ ставятся условия симметрии, т.е u=0 при x=0 (рис.1).
На границах ВС и CDставится граничные условия излучения [3,4], соответственно:
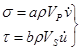и 
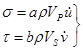(6)
где
σ и τ — нормальные и касательные напряжения;
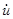и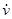 
— нормальные и касательные скорости частиц на границе,
Vp и Vs — скорости P и S волн;
a и b — безразмерные параметры;
ρ — плотность материала.
На границе ADприложена только одна сосредоточенная нагрузка, т. е.
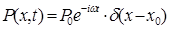
где Р0 — вектор заданной силы;
ω — частота внешних воздействий;
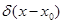— дельта-функция
Уравнения движения системы после разбиения области на конечные элементы записывается как обычно:
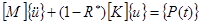(7)
С теоретической точки зрения представляет большой интерес сравнение результатов, полученных в двух предположения постановки задач. В качестве второго предположения рассмотрим уравнение с учётом диссипативных свойств грунта пропорционально скорости частиц.
Уравнения движения в этом случае записывается в следующем виде:
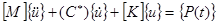(8)
Полученные результаты после решения уравнений (7) и (8) для различных типов грунтов приведены в таблице 1 для удобства сравнения полученных результатов приведены среднеарифметические значения отношений амплитуд вертикальных смещений поверхности грунта.
Здесь индекс «у» указывает, что результаты получены, когда матрица демпфирования пропорциональна матрице жесткости, т. е.
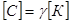
Индекс «в» указывает, что результаты получены в предположении, когда грунт обладает наследственными свойствами ползучести.
В обоих случаях учета вязкости грунта разница между ними составляет максимум 6 %. Это дает основание сделать следующее заключение, что исследователь при решении задач о распространении вибрации в грунте может выбрать любую из этих моделей по своему усмотрению.
Таблица 1
|
Частота, f |
Гравийно-песчаник, Ср.ар. (Vy/Vв) |
Лёсс, Ср.ар. (Vy/Vв) |
Суглинок, Ср.ар. (Vy/Vв) |
|
10 |
0,97 |
0,94 |
0,95 |
|
15 |
1,00 |
1,03 |
0,98 |
|
20 |
1,01 |
1,03 |
0,99 |
|
25 |
1,01 |
0,96 |
1,02 |
|
30 |
0,99 |
0,96 |
1,01 |
|
35 |
0,99 |
1,01 |
0,98 |
|
40 |
0,99 |
0,92 |
1,00 |
|
45 |
0,98 |
1,02 |
1,01 |
|
50 |
0,98 |
0,92 |
0,96 |
Физико-механические характеристики и параметры вязкости грунтов выбирались следующими:
для лёсса
Е=2,2·108 Па; ρ=1,79·103 н·с2/м4;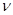 
=0,3
А=6,74·10–2, β=2,43·10–3, α=0,25
для гравийно-песчаника
Е=2,85·108 Па; ρ=1,87·103 н·с2/м4; 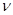=0,35
А=13,73·10–2, β=1,3·10–6, α=0,2
для суглинка
Е=4,21·108 Па; ρ=1,8·103 н·с2/м4; 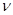=0,27
А=3,33·10–2, β=3,6·10–4, α=0,25
Анализ полученных результатов показал, что в лессовидном грунте амплитуда вибрационных волн затухает быстрее, чем в гравийно-песчаном или супеси. В достаточно удаленных от оси железнодорожная полотна точках поверхности грунта уровень вибрации существенно зависит от грунтовых условий: у прочных грунтов уровень вибрации поверхности грунта будет больше, чем у слабых.
Качественный анализ огибающих амплитуд колебания точек поверхности грунта показывает (рис.2), что все графики с увеличением расстоянии от оси симметрии имеют убывающий характер. С увеличением значения частоты внешних воздействий абсолютные значения амплитуды колебания поверхностных точек уменьшаются, и затухание происходит быстрее.
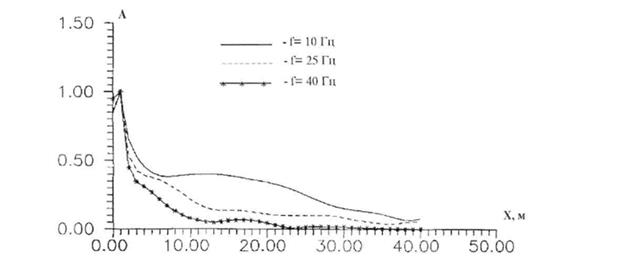
Рис. 2. Изменение огибающих амплитуд колебаний точек поверхности грунта
Литература:
1. Ильичев В. А., Юлдашев Ш. С., Саидов С. М. Исследование распространение вибраций от движения железнодорожных поездов в зависимости от расположения железнодорожного полотна. Оснований, фундаменты и механика грунтов, N2, М., Стройиздат,1999 г. с. 10–12
2. Ржаницын А. Р. Теория ползучести. М., Стройиздат, 1968, 416 с.
3. Lysmer J., Kyhlemeyer L. «Finite Dynamik Model for Infinite Media» Jour Engineering Mechanics Division, ASCE, Vol 95, No EM 4, August, 1969, p. 859–887.
4. Lysmer J, Udaka T, Tsai G-F, Seed H В «Flash-A Computer Program for Approimate 3-D Analysis of Soil-Strbctbre Interaction Problems», University of California, Berkelery, Repory No EERS 75–30, November, 1975.
