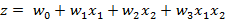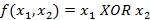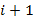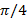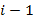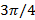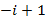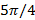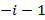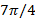Сегодня нейронные сети получили широкое распространение в мире. Они проникли во все сферы деятельности человека и вместе с этим привнесли новый способ обработки, анализа и прогнозирования данных.
В данной статье приводится описание преимуществ и возможностей использования комплексно-значных нейронов на примере решения задачи с оператором XOR. Комплексно-значная нейронная сеть — это сеть, основанная на комплексных числах, т. е. входные данные весы и функция активации являются комплексными.
На сегодняшний день существует три очень веские причины для использования комплексно-значных нейронов и нейронных сетей. Во-первых, в отличие от одного вещественного нейрона, один комплексно-значный нейрон может обучаться не линейно разделимым проблемам в начальном N-мерном пространстве, в котором они определены, без каких-либо нелинейных проекций на пространство с большей размерностью. Основываясь на этом, комплексно-значный нейрон является гораздо более функциональным, чем вещественный. Во-вторых, многие реальные проблемы, особенно в обработке сигналов, могут быть описаны правильно только в области частот, где комплексные числа также естественны, как целые числа при счете. В частотной области важно обработать амплитуду и фазу должным образом. Но на данный момент нет методов, чтобы использовать фазовое явление без комплексных чисел. Если мы хотим проанализировать любой процесс, в котором участвует фаза, мы определенно должны использовать комплексные числа и инструменты, которые подходят для работы с ними. Если мы обращаемся к фазе, как к вещественному числу из интервала [[0,2 π или [[, ππ -, то мы делаем большую ошибку, потому что в этом случае физическая природа фазы полностью теряет смысл. В-третьих, поскольку функциональность одного комплексно-значного нейрона выше, чем у одного вещественного нейрона, функциональность комплексно-значных нейронных сетей также выше, чем функциональность их вещественных аналогов. Меньшая комплексно-значная нейронная сеть может учиться быстрее и обобщать лучше, чем вещественная нейронная сеть. Это верно для однонаправленных комплексно-значных сетей и Хопфилд-подобных комплексно-значных сетей. Более функциональные нейроны, связанные в сеть, дают понять, что эта сеть также является более функциональной, чем его вещественной коллегой. В качестве примера можно рассмотреть однонаправленную многослойную нейронную сеть с комплексо-значными нейронами (ОМКЗНС) и однонаправленную многослойную нейронную сеть(ОМНС) Нейронная сеть Хопфилда с комплексо-значными нейронами и ее классический вариант. Однонаправленная многослойная нейронная сеть с комплексо-значными нейронами (ОМКЗНС) полностью превосходит однонаправленную многослойную нейронную сеть (ОМНС). Более того, ОМКЗНС учится быстрее и обобщает лучше, чем большей МФ. Кроме того, существует много проблем, которые ОМНС не может успешно решить, а ОМКЗНС может. Нейронная сеть Хопфилда с комплексо-значными нейронами может хранить гораздо больше моделей и имеет лучшую скорость извлечения ассоциативной памяти, чем классическая сеть Хопфилда. Кроме того, мы также видим, что лишь частично соединенная нейронная сеть с комплексо-значными нейронами также может быть использованы как очень мощная ассоциативная память.
Хотелось бы также сделать упор на некоторые ограничения, имеющиеся у вещественных нейронов и вещественных нейронных сетей. Наиболее важным из этих ограничений является невозможность одного вещественного нейрона обучаться не линейно разделимым данным ввода / вывода в начальном линейном N-мерном пространстве, в котором соответствующие данные ввода / вывода были определены. Классическим примером такой задачи является задача с оператором XOR. Она не может быть обучена с помощью одного вещественного нейрона. Из-за нелинейной отделимости вещественного нейрона.
Проблема XOR не может быть обучена с помощью одного вещественного порогового нейрона в начальном 2-мерном пространстве, но может быть обучена если 2-мерное пространство, будет нелинейно расширено до 3-х мерного пространства, добавив к двум входным данным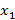 
и 
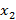нелинейное (квадратичное) третье входное данное 
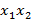, которое определяется как произведение двух исходных данных. Рассмотрим пространство (
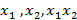), которое получается из 
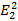, добавив квадратичный член, и, например, вектор весов W = (0,1,1,2). Это решение показано в таблице 1.
Таблица 1
Условия задачи XOR
|
|
|
|
|
sign(z) |
|
|
1 |
1 |
1 |
4 |
1 |
1 |
|
1 |
-1 |
-1 |
-2 |
-1 |
-1 |
|
-1 |
1 |
-1 |
-2 |
-1 |
-1 |
|
-1 |
-1 |
1 |
0 |
1 |
-1 |
На самом деле, это решение подтверждает теорему Ковера о разделимости образов, в которой говорится, что Нелинейное преобразование сложной задачи классификации образов в пространство более высокой размерности повышает вероятность линейной разделимости образов. На самом деле, все методы машинного обучения на базе ядра в том числе SVM основаны на этом подходе. Если какая-то проблема не является линейно разделимой в начальном n-мерном пространстве, где она определена (например, некоторые проблемы классификации, описанные в n особенностями), то можно проецировать не линейно на пространство более высокой размерности, в котором задача становится линейно разделимой. Любая однонаправленная нейронная сеть делает то же самое, но здесь может возникнуть вопрос возможно ли обучить нейрон для решения нелинейно разделимой задачи без расширения или преобразования исходного пространства? Ответ положителен, необходимо, просто перейти к комплексной области! Во всех нейронах и нейронных сетях, которые мы рассматривали до сих пор вес и входы являются вещественными и взвешенные суммы вещественны, соответственно. Рассмотрим теперь комплексно-значный вес. Таким образом, веса могут быть произвольные комплексные числа. Входы и выходы все еще будет вещественными. Кроме того, давайте рассмотрим узкий случай дискретных входов и выходов. Таким образом, наше отображение ввода / вывода описывается функцией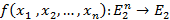 
, которая является логической функцией. Однако, так как наши веса — комплексные числа 
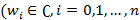) и входные данные — вещественные
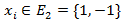, сумма произведений весов на входы дает комплексное число 
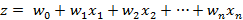, это значит что функция активация должна быть функцией от 
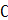к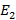 
. Давайте определим такую функцию следующим образом
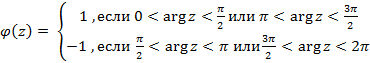(1)
где arg z является аргументом комплексного числа Z в диапазоне [0,2 π [. Очевидно,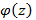 
приводит 
, 
: → 
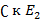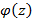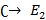. Функция активации (1,40) делит комплексную плоскость на 4 сектора, которые совпадают с четвертями комплексной плоскости, образованной его разделения с реальными и воображаемыми осями. В зависимости от arg z, 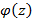равен 1 в 0-м и 2-м секторе (1-й и 3-й четверти), и -1 в 1-м и 3-м секторе (2-й и 4-й четверти). Вернемся к наиболее популярным классическим примером нелинейно разделимой задачи — XOR. Покажем, что один нейрон с функцией активации (1,40) можно легко реализовать нелинейно разделимой функции XOR без расширения оригинального 2-х мерного пространства. Возьмем вектор весов 
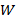= (0,
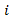,1) (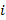
мнимая единица). Полученные результаты приведены в таблице 2.
Таблица 2
Результаты задачи
|
|
|
|
arg(z) |
|
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
-1 |
|
|
-1 |
-1 |
|
-1 |
1 |
|
|
-1 |
-1 |
|
-1 |
-1 |
|
|
1 |
-1 |
Эти результаты показывают, что проблема XOR, которая в течение многих лет, с одной стороны, была препятствием в теории нейронов, и, с другой стороны, была главным аргументом в пользу необходимости нейронных сетей из-за ограниченной функциональности одного нейрона, на самом деле может быть легко решена с помощью одного нейрона! Решение — это один нейрон с комплексно-значными весами! Это решение было впервые показано Игорем Айзенбергом в 1985 году [1]. Таким образом, способность одного нейрона с комплексно-значными весами решать не линейно разделимые задачи, как XOR ясно показывает, что комплексзначный нейрон имеет большую функциональность, чем один вещественной нейрон.
Литература:
1. Игорь Айзенберг Комплексно-значные нейроные сети — М.: Спрингер-Верлаг, 2011. — 279 с.
2. Джон Р. Фанчи, Математика для ученых и инженеров — 3-е издание — М.: Джон Вилли Корп., 2006. — 362с.
