В работе предприятия в условиях рыночной экономики и условиях обостренной конкурентной борьбы задача управления запасами является актуальной. В статье рассматриваются задачи управления запасами для дискретных и непрерывных моделей.
Ключевые слова: управление запасами, следящие системы, дискретная модель, непрерывная модель.
Введение
При функционировании любой экономической системы запасы различного рода играют важнейшую роль и возникают практически во всех звеньях народного хозяйства. Ни одно производственное предприятие не может существовать без материально-производственных запасов. Основные результаты производственной деятельности предприятия любой формы собственности зависят от объема и уровня запасов, реагируя на любые изменения рыночной конъюнктуры, и, главным образом, на соотношение спроса и предложения. Однако, не секрет, что иногда чрезмерное существование запасов приносит их владельцам лишь затраты и убытки.
Возникновение теории управления запасами принято связывать с работами Ф. Эджуорта и Ф. Харриса конца XIX - начала XX веков, в которых исследовалась простая оптимизационная модель для определения экономичного размера партии поставок для складской системы с равномерным постоянным расходом и периодическим поступлением хранимого продукта. В течение длительного времени эти работы оставались незамеченными, не находя ни теоретического развития, ни практического применения. Быстрое развитие этой теории началось в годы второй мировой войны и сразу после нее в рамках группы прикладных математических дисциплин, объединенных названием "исследование операций". В настоящее время теория управления запасами наиболее естественно рассматривается как раздел общей теории управления.
Значительный интерес к научному исследованию процессов запасания появился в середине прошлого века. Процессы управления запасами лишь кажутся простыми, и решения, построенные на интуиции, обычно далеки от оптимальных. Ненадежность интуиции в управлении процессами снабжения связана с двумя факторами:
1) со склонностью человека к накопительству, которая приобреталась им эволюционно (а в этих задачах "больше" далеко не всегда "лучше"),
2) с принципиальной стохастичностью почти всех реальных задач в этой области.
Целый ряд различных факторов определяет потребность в создании запасов: дискретный во многих случаях характер производства при непрерывном потреблении; необходимость согласования производственных процессов, протекающих с разной интенсивностью; многочисленные случайные возмущения (отказы оборудования, погодные и климатические воздействия, стихийные бедствия) и другие.
Экономика несет потери при неоправданно высоком уровне запасов из-за омертвления средств и замедления их оборачиваемости. Также нормальный ход производства нарушается при дефиците запасов, поскольку не хватает сырья и инструментов, и как результат срывается снабжение потребителей. Все это приводит к экономическому, социальному и моральному ущербу. Таким образом, для каждого вида хранимых ресурсов и каждого звена экономической системы существует оптимальный уровень запасов. Расчет таких наилучших уровней запасов, методов их создания и поддержания и является предметом теории управления запасами.
Теорию управления запасами можно рассматривать как инструмент, позволяющий наилучшим образом организовать процессы снабжения при заданных структурах хозяйственных связей и при механизмах планирования и экономического стимулирования. Существенно и обратное влияние - результаты решения задач управления запасами могут указывать направления организационно-экономических изменений, способствующих наилучшему функционированию систем снабжения.
В работах [1-5] для решения задач управления запасами применяются методы теории следящих систем управления.
Постановки задач управления запасами
1. Рассмотрим дискретную динамическую модель управления запасами для n типов товара на изолированном складе:
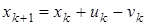 ,
,
где 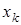 - это n-вектор запаса в k-м периоде работы системы,
- это n-вектор запаса в k-м периоде работы системы, 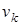 - это n-вектор спроса в k-м периоде работы системы,
- это n-вектор спроса в k-м периоде работы системы, 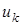 - это n-вектор поставок на склад в k-м периоде работы системы.
- это n-вектор поставок на склад в k-м периоде работы системы.
В работах [2, 4] исследовалась задача управления запасами с использованием методов пространства состояний. Модель спроса и канала наблюдений имела следующий вид:
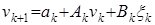 ,
,
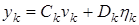 ,
,
где 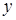 - m-вектор наблюдений за состоянием склада;
- m-вектор наблюдений за состоянием склада; 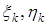 - независимые гауссовские векторы с независимыми компонентами с нулевыми средними значениями и единичными дисперсиями;
- независимые гауссовские векторы с независимыми компонентами с нулевыми средними значениями и единичными дисперсиями; 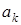 - известная векторная функция соответствующей размерности; Ak,Bk, Ck,Dk - известные матричные функции соответствующих размерностей.
- известная векторная функция соответствующей размерности; Ak,Bk, Ck,Dk - известные матричные функции соответствующих размерностей.
В [2, 4] рассмотрен алгоритм управления поставками товаров на склад, обеспечивающий заданный уровень запасов. Алгоритм основан на минимизации средней квадратичной ошибки. Ставится задача стабилизации на уровне 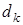 вектора запаса посредством выбора управления
вектора запаса посредством выбора управления 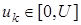 таким образом, чтобы критерий M{(
таким образом, чтобы критерий M{(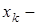
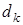 )T
)T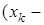
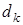 )} был минимальным (здесь М - оператор математического ожидания; индекс «T» обозначает тpaнcпониpовaниe).
)} был минимальным (здесь М - оператор математического ожидания; индекс «T» обозначает тpaнcпониpовaниe).
Используя теорию оптимальной линейной фильтрации случайных последовательностей и теорему разделения, получено следующее решение задачи:
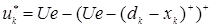 ,
,
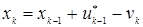 ,
,
где 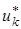 - оптимальное управление,
- оптимальное управление, 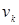 - наилучший в среднеквадратическом смысле прогноз вектора
- наилучший в среднеквадратическом смысле прогноз вектора 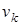 по наблюдениям
по наблюдениям 
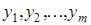 ,
, 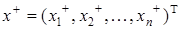 ,
, 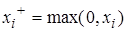 ,
, 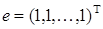 .
.
При оптимальном управлении запасы на складе удерживаются на заданном уровне.
2. В работе [3] рассмотрены задачи управления запасами для моделей в непрерывном времени, при этом использовался аппарат теории слежения в частотной области.
На основе информации о заказах и избытке или недостатке запасов ежедневно (непрерывно) издаются приказы о нормах выпуска продукции. Спустя некоторое время продукты, запущенные в производство в начальный момент времени, будут действительно изготовлены и войдут в состав запасов, причем продолжительность запаздывания определяется временем производства. Между тем из запасов ежедневно (непрерывно) изымаются товары для выполнения заказов потребителей. Информация о величине запасов подается обратно для ежедневного (непрерывного) сравнения с оптимальным уровнем запасов и вычисленная ошибка в свою очередь используется для уточнения планируемой скорости выпуска.
Эта система обладает характерными особенностями следящей системы. В ней имеется однонаправленная связь с нагрузкой и источником входного сигнала (заказы потребителей и заданные запасы). Она имеет цепь обратной связи:
ошибка ® планируемая продукция ® действительная продукция ® запасы ® ошибка.
Ошибка вызывает изменения в планируемой продукции, направленные к уменьшению ошибки.
Модель управления запасами описывается следующими уравнениями:
x(t) =K1[u(t) - v(t)], (1)
u(t) = K2[e(t)], (2)
e(t)= d(t) - x(t),
где K1 и K2 являются линейными операторами; d(t) - входной сигнал (заданная величина запасов); x(t) - действительные запасы готовой продукции, это выходной сигнал; ошибка e - дефицит запасов d(t) - x(t) (больше нуля или меньше нуля); v(t) - спрос, количество заказов потребителей в единицу времени; u(t) - поставки на склад в единицу времени t.
Уравнение (2) дает правило принятия решения - оно определяет объем планируемого (и фактически достигнутого) выпуска продукции в единицу времени как функцию избытка или недостатка запасов. Точный вид уравнения (1) определяется условиями задачи, поскольку по определению 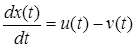 . Поэтому для конструирования следящей системы описанного класса, которая удовлетворяет некоторому критерию оптимальности, имеется в распоряжении только оператор K2 - правило принятия решения. Так как u(p) = K2(p)e(p), p - комплексная переменная, это правило на основе сведений о текущем избытке или недостатке запасов e(p) определяет, с какой скоростью u(p) следует продолжать производство. Пусть K2 =
. Поэтому для конструирования следящей системы описанного класса, которая удовлетворяет некоторому критерию оптимальности, имеется в распоряжении только оператор K2 - правило принятия решения. Так как u(p) = K2(p)e(p), p - комплексная переменная, это правило на основе сведений о текущем избытке или недостатке запасов e(p) определяет, с какой скоростью u(p) следует продолжать производство. Пусть K2 = 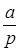 + b, где a, b - большие положительные константы. Вводя этот оператор в уравнение (2), получим
+ b, где a, b - большие положительные константы. Вводя этот оператор в уравнение (2), получим 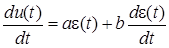 .
.
Это означает, что скорость выпуска нужно увеличить или уменьшить на величину, пропорциональную дефициту или избытку запасов, плюс величина, пропорциональная скорости уменьшения запасов. Коэффициенты пропорциональности a и b должны быть большими, если желательно поддерживать колебания запасов в узких пределах. Если необходимо избежать колебаний, должно выдерживаться соотношение 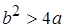 .
.
Анализируя литературу, можно сделать вывод, что ранее исследовались задачи управления запасами при точных или косвенных измерениях спроса. А задачи управления запасами при ненаблюдаемом спросе рассматривались только в непрерывном времени для однономенклатурного склада.
Заключение
Задача управления запасами является актуальной в работе предприятия в рыночных условиях и условиях обостренной конкурентной борьбы. Эффективность работы предприятия во многом зависит от количества товаров на складе: количество запасов на складе должно быть оптимальным - не мало, чтобы получить прибыль, и не много, чтобы товар не пролеживал на складе и не тормозил работу предприятия, тем самым неэффективно используя его оборотные средства.
Основные идеи теории следящих систем действительно могут быть использованы для анализа и разработки алгоритма управления производством.
Интенсивное развитие теории управления запасами и ее практическое применение в последние годы не оставляет сомнений в том, что данной прикладной научной дисциплине предстоит внести значительный вклад в повышение эффективности общественного производства.
ЛИТЕРАТУРА
1. Первозванский А.А. Математические модели в управлении производством. - М.: Наука, 1975.- 616 с.
2. Лотоцкий В.А. Управление запасами при частично наблюдаемом спросе // Статистические методы теории управления. - М.: Наука, 1978.- С. 222-224.
3. Симон Г.А. О применении теории следящих систем для изучения процессов регулирования производства // Процессы регулирования в моделях экономических систем: Сборник статей / ред. В. Я. Фридман, Л. П. Якименко. - М.: Изд-во иностранной литературы, 1961.- 290 с.
4. Лотоцкий В.А., Мандель А.С. Модели и методы управления запасами. - М.: Наука, 1991.- 189 с.
5. Рыжиков Ю.И. Теория очередей и управление запасами. - СПб.: Питер, 2001.- 376 с.







