Топологические модели представляет в виде графов. Граф-это фигура или конфигурация, образования совокупностью некоторых точек; некоторые из них могут быть соединены отрезками прямых, ломаных или кривых линий. Линии могут иметь направление.
Для химико-технологического процесса часто вершинами графа являются его элементы, а дуги показывают связь между элементами.
Количественный анализ надежности химико-технологических систем заключаются в определении вероятностно-статистических показателей надежности системы с применением результатов предварительного качественного анализа надежности ХТС. Качественный анализ надежности ХТС можно осуществить с помощью параметрического потокового графа (ППГ) ХТС, а количественный анализ надежности- с помощью топологической модели системы в виде параметрического графа надежности (ПГН) ХТС;
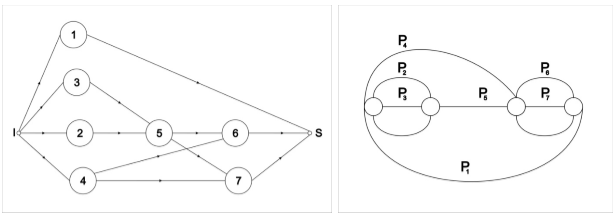
Рис. 1. Параметрический потоковый граф (а) и параметрический граф надежности (б) химико-технологической системы
ПГН ХТС-это неориентированный граф (рис.1), каждое 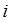 -е ребро которого соответствует
-е ребро которого соответствует  -му элементу ХТС, обладающему некоторой вероятностью безотказной работы
-му элементу ХТС, обладающему некоторой вероятностью безотказной работы 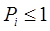 , а вершины ПГН отображают наличие технологических и информационных связей между элементами ХТС, которые считают абсолютно надежными:
, а вершины ПГН отображают наличие технологических и информационных связей между элементами ХТС, которые считают абсолютно надежными: 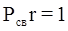 Положения каждого ребра в ПГН, соответствующего некоторому элементу ХТС, зависит от того, каким образом отказ этого элемента воздействует на отказ системы в целом, т. е. определяется влиянием характеристик надежности данного элемента на характеристику надежности ХТС.
Положения каждого ребра в ПГН, соответствующего некоторому элементу ХТС, зависит от того, каким образом отказ этого элемента воздействует на отказ системы в целом, т. е. определяется влиянием характеристик надежности данного элемента на характеристику надежности ХТС.
При анализе надежности ХТС с применением ПГН исходом из следующих предпосылок.
1. Отказы отдельных элементов ХТС независимы. Каждый отказ элемента приводит к отказу некоторой под системы ХТС или системы в целом.
2. Принимаем два виды отказов ХТС. Отказом ХТС первого вида будем считать событие, заключающееся в снижении производительности системы ниже заданной. Второй отказ соответствует событию, характеризующемуся полным прекращением выпуска продукции, т. е. выходом ХТС из строя.
3. Все элементы (подсистемы) ХТС будем классифицировать по влиянию отказов этих элементов (подсистем на надежность функционирования системы в целом. В соответствии с этим выделим следующие классы элементов: элементы подсистемы), отказы которых: а)не влияют на качество и количество выпускаемой продукции; б)приводят к отказу ХТС первого вида; в)вызывают отказ ХТС второго вида.
4. Поскольку при эксплуатации ХТС возможны оба вида отказов, то для одной технологической схемы ХТС будем строить два ПГН соответственно для отказа второго вида.
Согласно условно независимости отказов ХТС вероятность безотказной работы ХТС Р определим как произведение вероятностей отсутствия в системе отказов первого и второго видов Р1 и Р2
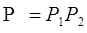
где, Р1 и Р2 определяется с помощью соответствующих ПГН ХТС.
С учётом этих предпосылок методика построения ПГН для отказов ХТС первого и второго вида, осуществляемого по исходному ППГ ХТС, состоит из следующих операций.
В ППГ выделим вершины, соответствующие тем элементам системы, отказ которых вызывает отказ ХТС в целом, т. е. выделим вершины ППГ, соответствующие основному технологическому потоку между элементами ХТС от входа сырья 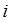 до выхода готовой продукции S. Этим вершинам ППГ ставим в соответствие последовательное соединение ребер ПГН ХТС. Среди остальных вершин ППГ выделим вершины, соответствующие резервным элементам ХТС, которым ставят в соответствие в ПГН ребра, параллельные ребрам основного соединения.
до выхода готовой продукции S. Этим вершинам ППГ ставим в соответствие последовательное соединение ребер ПГН ХТС. Среди остальных вершин ППГ выделим вершины, соответствующие резервным элементам ХТС, которым ставят в соответствие в ПГН ребра, параллельные ребрам основного соединения.
Для ХТС, структурная схема которой представлена на рис 2, а, соответствующие ей ППГ и ПГН изображены на рис 2, в-г. ПГН для отказа ХТС первого вида (рис.2,в) представляют собой последовательное соединение всех ребер, так как отказ любого элемента данный ХТС снижает её производительность. В ПГН (рис.2,г) ребра Р1,Р2,Р4 и Р5 соединены последовательно, так как элементы 1,2,4 и 5 образуют основное соединение ХТС. Ребра 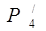 параллельно ребру Р4, так как элемент 4/ является резерным но отношению к основному элементу 4. Ребро Р3 ответвляется от основного соединения ребер ПГН, так как оно соответствует элементу 3, отказ которого не вызывает отказа ХТС второго вида.
параллельно ребру Р4, так как элемент 4/ является резерным но отношению к основному элементу 4. Ребро Р3 ответвляется от основного соединения ребер ПГН, так как оно соответствует элементу 3, отказ которого не вызывает отказа ХТС второго вида.
ПНГ, соответствующий отказу ХТС первого вида, позволяет определить вероятность функционирования ХТС с заданной производительностью. На рис.3,а представлена структурная схема ХТС производства продукта С, образующегося в реакторе 2 из полупродукта А/, три партии которого получают в реакторах 1,1/ и 1//. Если, например, для непрерывной работы реактора 2 достаточно двух партий полупродукта А/, то отказа ХТС первого вида возникает лишь при отказе химических реакторов, в которых производится полупродукт А/. Указанным условиям функционирования ХТС отвечает ПГН, изображенный на рис. 3 в.
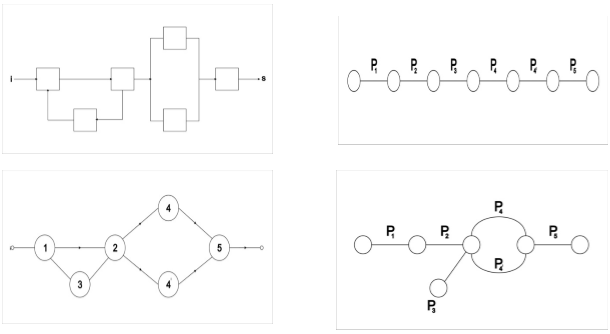
Рис. 2. Структурная схема(а), параметрический потоковый граф (б) и параметрические графы надежности химико-технологической системы для отказов первого вида (в) и второго вида (г); 1,4,4-химические реакторы; 2-сепаратор; 5-холодильник
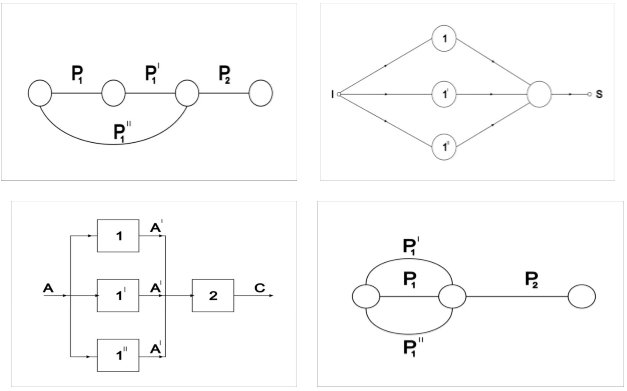
Рис. 3. Структурная схема (а), параметрический потоковый граф (б) и параметрические графы надежности (в,г) ХТС производства продукта С: 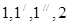 -химические реакторы; А-исходное сырьё; А/-полупродукт
-химические реакторы; А-исходное сырьё; А/-полупродукт
ПГН, соответствующий отказу ХТС второго вида, позволяет определить вероятность функционирования ХТС без прекращения выпуска продукции или без отклонения качественных показателей продукта за пределы, допускаемые техническими условиями. Например, для ХТС, структурная схема который представлена на рис. 3,а, отказ второго вида наступает, если откажут одновременно все три химических реактора, производящих полуфабрикат А/. На рис.3,г. изображен ПГН, соответствующий этому случаю. На рис 4,а изображена структурная схема многоконтурной ХТС производства продукта В. Элементы 1,2 и 3 являются основными элементами данной системы, а 4 и 5- вспомогательными.
Отказ вспомогательных элементов вызывает отказ системы первого вида, а отказ любого из основных элементов приводит к отказу ХТС второго вида.
Таким образом, структурной схеме некоторой ХТС в зависимости от показателей надежности её функционирования могут соответствовать различные структуры ПГН. В общем случае независимо от отказов ХТС для различных вариантов структуры ПНГ возможны структуры ПНГ, представляющие только лишь последовательное, параллельное или смешанное соединение ребер.
Другой топологической моделью применяемой для количественного анализа надежности ХТС, является дуальный ПГН, который позволяет определить зависимость надежности ХТС, является дуальный ПГН, который позволяет определить зависимость надежности ХТС от надежности технологических связей системы. Так же, как и в случае отказов элементов ХТС, отказы технологических связей (разрыв, замерзание или забивание трубопроводов, пропуски в сварных соединениях и другие) вызывает отказы от ХТС первого или второго видов.
Дуальный ПГН ХТС- это неориентированный граф, в котором каждому 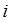 -му ребру, отображающему
-му ребру, отображающему 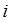 -ю технологическую связь, соответствует число
-ю технологическую связь, соответствует число 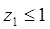 , равное вероятности исправного действия этой технологической связи. При построении дуального ПГН соблюдается тот же порядок, что и при построении ПГН ХТС, но только по отношению к технологическим связям.
, равное вероятности исправного действия этой технологической связи. При построении дуального ПГН соблюдается тот же порядок, что и при построении ПГН ХТС, но только по отношению к технологическим связям.
Для определения вероятности безотказной работы ХТС, с помощью ПГН можно использовать символическое исчисление [2], в котором приняты условные операции, отображающие некоторые алгебраические операции. Для независимых отказов элементов ХТС вводят условные операции умножения и сложения
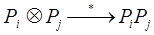 (2)
(2)
где 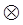 -условная операция умножения для определения вероятности безотказной работы элементов ХТС, которым ПНГ соответствует последовательное соединение ребер (элементарная цепь графа);
-условная операция умножения для определения вероятности безотказной работы элементов ХТС, которым ПНГ соответствует последовательное соединение ребер (элементарная цепь графа);
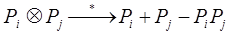 (3)
(3)
где 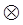 -условная операция сложения для определения вероятности безотказной работы элементов ХТС, которым в ПГН соответствуют параллельные ребра.
-условная операция сложения для определения вероятности безотказной работы элементов ХТС, которым в ПГН соответствуют параллельные ребра.
Символическое исчисление позволяет формализовать вывод зависимости вероятности безотказной работы ХТС 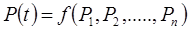 где Рi-вероятность безотказной работы
где Рi-вероятность безотказной работы 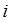 -го элемента,
-го элемента,
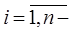 число элементов ХТС, причем полученная зависимость, представленная в символической форме, сохраняет информацию о топологии ПГН в отличие от окончательной алгебраической формы, в которой не отражаются топологические характеристики ПГН.
число элементов ХТС, причем полученная зависимость, представленная в символической форме, сохраняет информацию о топологии ПГН в отличие от окончательной алгебраической формы, в которой не отражаются топологические характеристики ПГН.
Для ХТС с большим числом элементов и технологических связей между ними ПГН имеют сложную структуру. Поэтому получить зависимость вероятности безотказной работы ХТС от вероятностей безотказной работы элементов ХТС на основе преобразования топологии ПГН с применением символического исчисления возможно только лишь с исползованнем ЭВМ.
Литература:
1. Кафаров В. В., Перов В. Л., Мешалкин В. П. Принципы математического моделирования химико-технологических систем.-М.:Химия,1974
2. Жаворонков Н. М., Кафаров В. В., Леров В. Л., Мешалкин В. П. Теоретические основы химической технологии., 4,№ 2,152(1970)







