В работе представлены закономерности влияния концентрации аппрета, продолжительности изотермической выдержки и объёмной степени наполнения на деформативные свойства серных композитов на аппретированном кварцевом наполнителе.
Ключевые слова: серные композиты, деформативные свойства.
В работе приведены результаты исследования влияния концентрации аппрета (каучука марки СКДН-Н), продолжительности изотермической выдержки и объёмной степени наполнения на деформативные свойства серных композитов на аппретированном кварцевом наполнителе. Определение влияния указанных факторов на модуль упругости, модуль деформации и прогиб при максимальной нагрузке проводили с применением метода математического планирования эксперимента. Для этого был спланирован и реализован полный трехфакторный эксперимент. В качестве варьируемых факторов были выбраны следующие рецептурно-технологические факторы (табл. 1): Х1 — продолжительность изотермической выдержки, ч; Х2 — концентрация раствора аппрета, %; Х3 — объёмная доля кварцевой муки с Sуд =180 м2/кг.
Таблица 1
Матрица планирования эксперимента в кодовом и натуральном выражениях
|
№ п/п |
Значения факторов в кодовом выражении |
Значения факторов в натуральном выражении |
||||
|
X1 |
X2 |
X3 |
X1 |
X2 |
X3 |
|
|
1 |
-1 |
-1 |
-1 |
1 |
10 |
0,3 |
|
2 |
1 |
-1 |
-1 |
3 |
10 |
0,3 |
|
3 |
-1 |
1 |
-1 |
1 |
50 |
0,3 |
|
4 |
1 |
1 |
-1 |
3 |
50 |
0,3 |
|
5 |
-1 |
-1 |
1 |
1 |
10 |
0,4 |
|
6 |
1 |
-1 |
1 |
3 |
10 |
0,4 |
|
7 |
-1 |
1 |
1 |
1 |
50 |
0,4 |
|
8 |
1 |
1 |
1 |
3 |
50 |
0,4 |
Значения модуля упругости, модуля деформации и прогиба при максимальной нагрузке для исследуемых составов приведены в табл. 2.
Таблица 2
Значения модуля упругости, модуля деформации и прогиба при максимальной нагрузке для исследуемых составов
|
№ п/п |
Модуль упругости, МПа |
Модуль деформации, МПа |
Прогиб при максимальной нагрузке, мм |
|
1 |
6492 |
1688 |
0,032 |
|
2 |
18870 |
2796 |
0,060 |
|
3 |
7640 |
2069 |
0,039 |
|
4 |
19789 |
3500 |
0,096 |
|
5 |
10320 |
1601 |
0,030 |
|
6 |
23156 |
2179 |
0,030 |
|
7 |
11203 |
2634 |
0,042 |
|
8 |
24333 |
3710 |
0,070 |
Расчёт коэффициентов уравнений регрессии и их статистический анализ проводился на ЭВМ с помощью программного комплекса «Градиент»:
— для модуля упругости, МПа
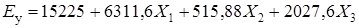; (1)
– для модуля деформации, МПа
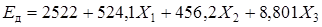; (2)
– для прогиба при максимальной нагрузке, мм
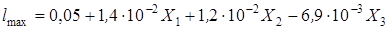. (3)
Анализ уравнения регрессии (1) показывает, что увеличение концентрации аппрета (фактор Х2) и продолжительности изотермической выдержки (фактор Х1), а также объёмной доли (фактор Х3) приводит к повышению модуля упругости. Необходимо отметить, что с увеличением продолжительности изотермической выдержки происходит переход кристаллических модификаций серы в полимерную [1], которая имеет более высокие показатели деформативных свойств (модуль упругости меньше). Отсюда целесообразно предположить, что фактор Х1 будет оказывать отрицательное влияние на исследуемые свойства композитов. Однако этого не наблюдается, что можно объяснить следующим образом. В процессе изготовления серного материала на аппретированном кварцевом наполнителе происходит серная вулканизация аппрета, в результате образуется слой вулканизата, объёмные деформации которого практически обеспечивает свободную усадку оболочки серы [2]. Это, в свою очередь, создаёт предпосылки для формирования кристаллической структуры серы в равновесных условиях, имеющей менее дефектную структуру, а, следовательно, с наименьшим количеством напряжённых элементов в композите.
Наибольший модуль упругости имеют составы, изготовленные на кварцевой муке, обработанной высококонцентрированными растворами аппрета (0,6 и 1 % от массы серы) и подвергшиеся изотермической выдержке в течение 2…3 ч: 19000….24000 МПа.
Из уравнения регрессии (2) видно, что исследуемые факторы оказывают на модуль деформации аналогичное влияние, которое также объясняется в рамках выше приведенной физической модели.
Аппретирование поверхности наполнителя (фактор Х2) и продолжительность изотермической выдержки (фактор Х1) приводит вследствие увеличения количества полимерной составляющей (образования полимерной серы и вулканизата) к повышению величины прогиба при максимальной нагрузке (уравнение (3)). Введение наполнителя (фактор Х.3) изменяет при прочих равных температурно-временных условиях содержание полимерной фазы (рис. 1). Для расчёта количества полимерной составляющей принята следующая модель
,
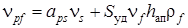где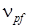 
– объёмная доля полимерной составляющей; 
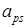– коэффициент, характеризующий образование полимерной серы в принятых температурно-временных условиях; 
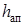– толщина аппрета (вулканизата); 
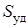– удельная поверхность наполнителя; 
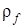– средняя плотность наполнителя.
С учетом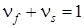 
количество 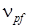определится
.
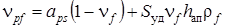Из рис. 1 видно, что с увеличением объёмной степени наполнения количество полимерной составляющей уменьшается. Это и обусловливает антогонистическое влияние и весомость фактора Х.3.
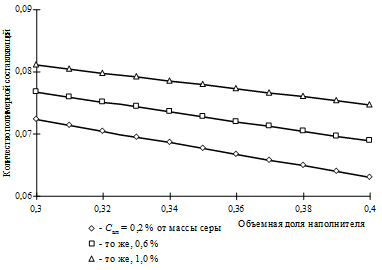
Рис. 1. Зависимость количества полимерной составляющей от степени наполнения материала (при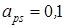 
)
Литература:
1. Патуроев В. В. Серные бетоны и бетоны, пропитанные серой [Текст] / В. В. Патуроев, А. Н. Волгушев, Ю. И. Орловский // Обзорная информация. — М.: ВНИИИС. — Вып. 1, 1985. — 58 с.
2. Шитова И. Ю. Внутренние напряжения в наномодифицированных серных композиционных материалах [Текст] / Е. Н. Самошина, К. Н. Махамбетова // Современные проблемы науки и образования. — 2015. — № 1; URL: http://www.science-education.ru/121–17131.
