Демографическая тема сегодня одна из наиболее актуальных как на территории РФ, так и во всем мире. Данному вопросу посвящено множество рубрик в газетах, научных журналах, радио и телепрограмм.
Для подтверждения или опровержения мнения об отрицательной тенденции становления российской демографии обратимся к статистике. Институт демографических исследований Москвы составил прогнозы двух путей развития демографии России (таблица 1)
Таблица 1
Прогнозы развития демографии России
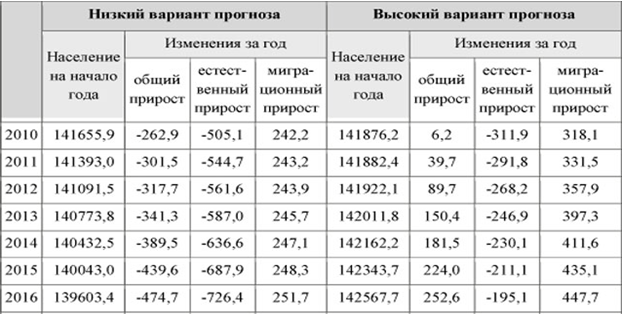
Прогнозы развития демографии России, представленные в таблице 1, отражают тенденцию к спаду численности коренного населения страны. Стоит отметить, что общий прирост населения РФ происходит за счёт возросшего числа прибывших иммигрантов из стран ближнего зарубежья.
Обратимся к демографической ситуации Самарской области и составим прогноз дальнейшего развития такого показателя, как рождаемость.
Таблица 2
Показатели рождаемости по Самарской области за 2005–2014 гг. (тыс. чел.).
|
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
|
32,41 |
31,25 |
32,10 |
35,00 |
37,43 |
37,80 |
39,25 |
38,46 |
40,25 |
46,76 |
По данным из таблицы 2 можно сделать вывод о том, что существует положительная тенденция развития показателя рождаемости.
Для дальнейшего составления прогноза необходимо произвести сглаживание по 5 точкам (см. таблицу 4)
Таблица 3
Y0 = 1/5*(Y-2+Y-1+Y0+Y+1+Y+2) — уравнение средних точек ФОРМУЛЫ ПО 5-И ТОЧКАМ
Y-1 = 1/10*(4Y-2+3Y-1+2Y0+Y+1)
Y+1 = 1/10*(Y-1+2Y0+3Y+1+4Y+2)
Y-2 = 1/5*(3Y-2+2Y-1+Y0-Y+2)
Y+2 = 1/5*(-Y-2+Y0+2Y+1+3Y+2)
Таблица 4
Показатели сглаживания рождаемости по Самарской области по 5-и точкам
|
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
|
30,88 |
32,26 |
33,64 |
34,72 |
36,32 |
37,59 |
38,64 |
40,50 |
42,40 |
44,29 |
Построим график основного и сглаженного рядов (рис.1)
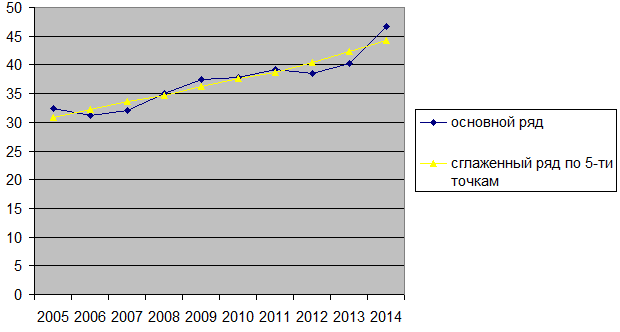
Рис. 1. График основного и сглаженного рядов
Перед построением модели необходимо произвести расчеты, позволяющие вскрыть наличие тенденции в сглаженном по 5-ти точкам ряду.
Используем метод сравнений средних уравнений. Данный ряд разбиваем на 2 равные части и по каждой части находим среднее значение.
Yс1=Сумм Yt/nYс2=Сумм Yt/n
|
Y ср1 |
30,88 |
32,26 |
33,64 |
34,72 |
36,32 |
33,56 |
|
Y ср2 |
37,59 |
38.64 |
40,50 |
42,40 |
44,29 |
40,68 |
Затем находим значения исправленных дисперсий для каждой части ряда.
S1,22=(Сумм(Yt-Yср.1,2)2)/n1,2–1, где t — уровни динамического ряда;
n — число членов динамического ряда; n1,n2 — число членов в 1-ой и 2-ой части
S12=((30,88–33,56)2+(32,26–33,56)2+…+(36,32–33,56)2)/4=4,46
S22=((37,59–40,68)2+(38,64–40,68)2+…+(44,29–40,68)2)/4=7,43
Проверим гипотезу о равенстве дисперсии S12 и S22 для этого необходимо определить расчетное значение Fрасч.:
Fрасч.= Smax2/Smin2 = 7,43/4,46 =1,67
И сравним его с табличным критерием при заданном уровне значимости a<=0.05
Если Fрасч<Fтабл. (1,67<6,39), расхождения между дисперсиями случайны, т. е. тренд существует.
Теперь рассчитаем показатель Стьюдента: Tрасч.>Tтабл., где Tтабл.=2,31
S= √((19*4,46+16*7,43)/8)*√(1/5+1/5)=3,07
Tрасч.= (40,68–33,56)/3,07=2,31, следовательно Tрасч.= Tтабл., т. е. 2,31=2,31
Теперь определим первые средние приросты: U=(Yt+1-Yt-1)/2,где (t=2…n-1)
Решение:
U2006= (33,64–30,88)/2=1,38
U2007= (34,72–32,26)/2=1,23
U2008= (36,32–33,64)/2=1,34
U2009= (37,59–34,72)/2=1,44
U2010= (38,64–36,32)/2=1,16
U2011= (40,50–37,59)/2=1,46
U2012= (42,40–38,64)/2=1,88
U2013= (44,29–40,50)/2=3,79
Таким образом, мы видим, что первые средние приросты являются зависимыми, за исключением U2013 он равен 3,79, следовательно, используется линейное уравнение прямой.
Таблица 5
Рождаемость в Самарской области, тыс.чел.
|
|
t |
ИТОГО |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
55 |
|
|
y |
32,41 |
31,25 |
32,10 |
35,00 |
37,43 |
37,80 |
39,25 |
38,46 |
40,25 |
46,76 |
370,71 |
|
yt |
32,41 |
62,50 |
96,30 |
140,00 |
187,15 |
226,80 |
274,75 |
307,68 |
362,25 |
467,60 |
2157,44 |
|
y2 |
1050,40 |
976,56 |
1030,41 |
1225,00 |
1401,01 |
1428,84 |
1540,56 |
1479,17 |
1620,06 |
2186,50 |
13938,51 |
Вводим ещё один динамический ряд, влияющий на рождаемость по Самарской области — браки (см. таблицу 6)
Таблица 6
Браки в Самарской области, тыс.чел.
|
|
t |
ИТОГО |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
55 |
|
x |
22,40 |
24,80 |
25,90 |
29,40 |
27,70 |
27,00 |
27,50 |
30,20 |
32,20 |
35,30 |
284,40 |
|
xt |
22,40 |
49,60 |
77,70 |
117,60 |
138,50 |
162,00 |
192,50 |
241,60 |
289,80 |
353,00 |
1644,70 |
|
х2 |
501,76 |
615,04 |
670,81 |
864,36 |
767,29 |
729,00 |
756,25 |
912,04 |
1036,84 |
1246,09 |
8099,48 |
|
ху |
725,98 |
775,00 |
831,39 |
1029,00 |
1036,81 |
1020,60 |
1079,38 |
1161,49 |
1296,05 |
1650,63 |
10606,33 |
Уравнение прямой, описывающей влияние показателя рождаемость и браки выглядит следующим образом: y=a0+a1x+a2t
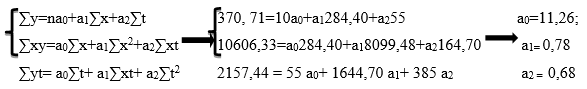
Для наглядности и удобства расчётов составляем таблицу 7, в которую заносим показатель рождаемости (у) и показатель заключения браков (х).
Таблица 7
|
№ |
y |
x |
y2 |
^y |
^y2 |
отклонение |
|
|
(y-^y)2 |
(y-^y)*100 |
||||||
|
1 |
32,41 |
22,40 |
1050,40 |
29,41 |
864,95 |
9,00 |
118,24 |
|
2 |
31,25 |
24,80 |
976,56 |
31,96 |
1021,44 |
0,50 |
97,78 |
|
3 |
32,10 |
25,90 |
1030,41 |
33,50 |
1122,25 |
1,96 |
95,82 |
|
4 |
35,00 |
29,40 |
1225,00 |
36,91 |
1362,35 |
3,65 |
94,83 |
|
5 |
37,43 |
27,70 |
1401,01 |
36,27 |
1315,51 |
1,35 |
103,20 |
|
6 |
37,80 |
27,00 |
1428,84 |
36,40 |
1324,96 |
1,96 |
103,85 |
|
7 |
39,25 |
27,50 |
1540,56 |
37,47 |
1404,00 |
3,17 |
104,75 |
|
8 |
38,46 |
30,20 |
1479,17 |
40,25 |
1620,06 |
3,20 |
95,55 |
|
9 |
40,25 |
32,20 |
1620,06 |
42,49 |
1805,40 |
5,02 |
94,73 |
|
10 |
46,76 |
35,30 |
2186,50 |
45,59 |
2078,45 |
1,37 |
102,57 |
|
55 |
370,71 |
284,40 |
13938,51 |
370,25 |
13919,37 |
0,21 |
100,12 |
|
ИТОГО |
|||||||
Найдем тесноту связи между показателями рождаемости и браков.
δ2общ(y)=(∑у2/n) — y2=(13938,51/10)-1374,26=19,59
δ2факт(y)=(∑^у2/n) — y2=(13919,37/10)-1374,26=17,68
δ2ост(y)=δ2общ(y)- δ2факт(y)=19,59–17,68=1,91
Определение тесноты связи между критериальной переменной и регрессором. Теснота связи равна 0,95. Что свидетельствует о тесной связи между анализируемыми показателями.
Произведём расчет ошибок по формуле:
Средняя относительная ошибка аппроксимации: m=(1/n(∑ (y-^у)/y))*100
m= 1/10* (370,71–37,07)/370,71 *100=0,01
Расчёт средней относительной ошибки аппроксимации, её значение равно 0,01, что свидетельствует о высокой точности прогнозной модели.
Составим прогноз развития рождаемости по Самарской области.
Уравнение показателя рождаемости имеет следующий вид: у = 11,26+0,78х+0,68t
у = 11,26+0,78*34,95+0,68*11= 46
у = 11,26+0,78*34,59+0,68*12=46,40
у = 11,26+0,78*34,24+0,68*12=46,81
Таким образом, составив прогноз рождаемости по Самарской области, можно сделать вывод о том, что данный показатель имеет тенденцию к увеличению, что положительно отразиться на развитии демографической ситуации региона.
Стоит ещё раз отметить, что демография — одна из важнейших составляющих полноценного развивающегося общества. Огромное количество мероприятий проводиться для поддержания и улучшение демографии не только регионов, областей, но и страны в целом. Будущее Самарской области будет зависеть от правильности решений задач, возникающих с появлением демографических перепадов.
Литература:
1. Форрестер Дж. Динамика развития города.- М., 2012
2. Кучмаева, О. В. Статистический мониторинг положения детей в Российской Федерации [Текст]/ О. Л. Петрякова, Е. А. Марыганова// Вопросы статистики.-2012-№ 1.-С. 61–68.
3. Российская экономика в 2012–2013гг.: тенденции, анализ, прогноз [Текст]/ Н. Н. Райская [и др.]// Вопросы статистики.-2013-№ 1.-С. 45–60.
4. Демографическая ситуация Самарской области [Электронный ресурс]//Самарстат. — Режим доступа: http://samarastat.gks.ru







