Рассматривается постановка лабораторной работы, связанной с моделированием движения транспортного робота по квазиоптимальной траектории при недостаточной априорной информации и при наличии неконтролируемых возмущений. Работа предназначена для студентов технических ВУЗов по дисциплине «Моделирование робототехнических систем».
В настоящее время широкое распространение среди студентов получили международные соревнования роботов. Разработано значительное число вариантов проведения робототехнических соревнований, в которых состязаются различные типы роботов с различными целевыми функциями [1].
Основной целью проведения соревнований является определение наиболее эффективного робота, который способен, согласно регламенту, победить своих соперников. На уровне планирования движения робота предполагаются известными: цель движения, наличие различных датчиков внешней среды и описание полигона — пункты обхода и возможные препятствия. Для построения наилучшей траектории движения используются различные интуитивные алгоритмы действий.
Одним из таких видов соревнования является «Слалом по линии», регламент этого вида соревнований содержит в себе условия состязания роботов, требования к характеристикам робота и к полигону, правила отбора победителя [2].
Роботу необходимо за наиболее короткое время пройти трассу (рис.1), от начала до конца, при наличии на трассе препятствий (в данном случае — кегли). Робот должен обходить препятствия попеременно с правой и с левой сторон, не допуская столкновения. На финише могут быть установлены ворота, которые необходимо также аккуратно не задевая пройти. Максимально допустимое время прохождения дистанции — 3 минуты.
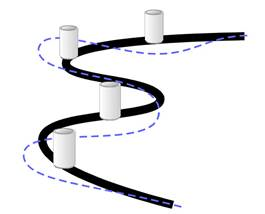
Рис. 1. Полигон «Слалом по линии»
На наш взгляд, при фиксированной курсовой скорости, минимизировать время прохождения трассы возможно за счет:
- уменьшения угла рысканья при движении по нелинейной траектории;
- учета инерционности робота при обходе препятствий (заблаговременно спланировать траекторию обхода с минимальным допустимым приближением к нему);
- при случайном расположении препятствий спланировать оптимальную, в смысле кратчайшего пути, траекторию обхода;
- в усложненном варианте, когда положение препятствий выявляется самим роботом с помощью некоторого датчика, потребуется решать задачу коммивояжера при недостаточно априорной информации.
Следование робота по определённому маршруту — это важная задача в робототехнике. В данной работе моделируется движение робота по найденной квазиоптимальной траектории, которая проходит по заданным точкам. Особенности модели состоят в том, что робот инерционный (не может мгновенно изменить курсовую скорость) и на него действуют помехи.
Для реализации решения задачи создана программа, в которой отображается движение робота по заданной траектории с «вихлянием» на трассе из-за действия помех, могут происходить «заносы» при поворотах и могут появляться в произвольный момент времени новые маяки.
Примером реальных задач могут быть: обслуживание раненых на поле боя, где необходимо минимальное время обслуживания и учет срочности оказания медицинской помощи. В связи с этим, проведены исследования с целью выяснения помех и синтез фильтров, уменьшающих это влияние.
Описательная постановка задачи
Предполагается, что робот должен обойти контрольные точки и вернуться в исходную позицию по оптимальной траектории. Критерий оптимальности: минимальный пройденный путь или минимальное время прохождения траектории.
Однако, робот подвергается воздействию помех: на него действуют внешние силы, отклоняющие от заданной траектории (непроходимые участки местности, ветер — для летательных аппаратов, течение — для морского робота).
Координаты опорных точек робот определяет с помощью некоторого датчика радиально-кругового обзора. Но при нахождение в начальной точке, робот может не видеть некоторые контрольные точки, если они скрыты за местными объектами. В процессе движения они могут появляться в поле зрения робота и тогда он их запоминает.
Координаты могут определяться с ошибками по дальности и по углу. Т. е. робот будет ориентироваться не на истинное положение объекта, а на видимое с его точки зрения в данный момент.
Обход контрольных точек по оптимальной траектории — это известная задача «Коммивояжера». Она формулируется очень просто: на плоскости расположены N городов и заданы расстояния между ними. Требуется найти маршрут минимальной длины с посещением каждого города ровно один раз и с возвращением в исходную точку. В классической задаче коммивояжера целевой функцией, которую надо минимизировать, является стоимость обхода.
Но в нашем случае задача усложняется за счет отсутствия полной информации о положении контрольных точек.
Еще одна сложность связана с тем, что мы моделируем движение не идеального робота, а инерционного, что приводит к отклонению реальной траектории от заданной при движении по нелинейному маршруту.
Уточненная постановка задачи моделирования движения робота
Построить динамическую программную модель обхода роботом опорных (контрольных) точек по оптимальной, в заданном смысле, траектории. При этом предполагается следующее.
- Робот движется в плоскости.
- На этой плоскости задаются координаты опорных точек.
- В начальный момент виртуальный Робот (Клиент) считывает координаты опорных точек и выдает их в программу Оптимум (Сервер)
- Программа Оптимум вычисляет оптимальную (в заданном смысле) траекторию и выдает в программу Робот последовательность обхода указанных точек.
- Предполагается, что количество опорных N точек задано, но в начальный момент программа Оптимум получает расстояния лишь среди К точек, остальные M = N-K могут добавляться в процессе движения робота по траектории. Выполняется соотношение: M ≥ 0 и M < K ≤ N.
- На первом этапе решается классическая задача коммивояжера.
- Полученное решение, т. е. последовательность обхода контрольных точек выдается модулю Робот.
- Получив информацию, робот начинает движение и может обнаружить новые контрольные точки (например, новые цели).
- Информация о них выдается модулю Оптимум.
- Задача коммивояжера перестает быть классической и требуется модернизация алгоритма ее решения.
- Новый порядок оптимального обхода передается роботу.
- Робот — инерционный, т. е. наброс скорости (максимальное изменение скорости за один цикл управления) ограничен.
- На робот (или на координаты опорных точек воздействуют неконтролируемые помехи с заданными параметрами распределения. Т. е. требуется разработать адаптивные алгоритмы управления, минимизирующие влияние внешних воздействий на качество управления.
Математическая постановка задачи
Имеется n контрольных точек с номерами 1,2,…n, для каждой пары точек i и j задано расстояние c [i, j] между ними. Выходя из первой точки, робот должен побывать во всех остальных контрольных точках по одному разу и вернуться в исходную.
Требуется определить, в каком порядке следует обходить контрольные точки, чтобы суммарное пройденное расстояние (или время обхода) было бы наименьшим.
Для решения данной задачи, в интегрированной среде визуального программирования Delphi 7, была реализована компьютерная модель «Планирование оптимального маршрута транспортного робота» (рис. 2), состоящая из двух модулей. Первый модуль предназначен для студентов и позволяет проводить лабораторную работу по решению задачи о коммивояжере, этот модуль может осуществлять проверку результата. Другой модуль, предназначенный исключительно для преподавателя, решает задачу автоматически выбранным методом.
Интерфейс программного модуля Оптимум позволяет:
- задавать матрицу расстояний или получать ее от виртуальной модели робота (модуль Робот),
- задавать алгоритм расчета оптимальной траектории (метод ветвей и границ, полный перебор, жадный алгоритм),
- выводить графическое отображение результатов,
- отправлять сигнал о готовности модулю «Робот»,
- зафиксировать время, затраченное на расчет выбранным алгоритмом в формате (мин.: сек.: миллисек.).
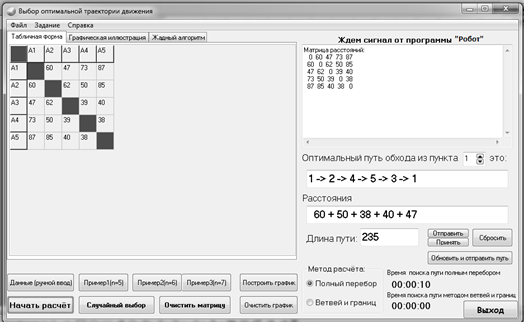
Рис. 2. Окно программы «Выбор оптимальной траектории движения робота»
Программа получает от модуля Робот матрицу расстояний, обрабатывает её и отсылает обратно оптимальный путь обхода.
В случае возникновения новых данных появляется сигнал «обнаружена новая точка», после чего Робот должен «принять» информацию и отправить в обработку.
Математическая модель нестационарной задачи оптимизации строится как декомпозиция сменяющих друг друга стационарных задач. Предыдущий результат оптимального пути «обновляется и отсылается» программе Робот для графического отображения извлеченной информации.
Интерфейс программной модели Робот при наличии внешних помех представлен на рис. 3.
Виртуальный робот снабжен датчиком радиально-кругового обзора. Особенности такого датчика накладывают ограничение на восприятие местности: при нахождении в конкретной точке робота некоторые опорные точки могут быть невидимы из-за наличия других объектов. Координаты всех обнаруженных опорных точек запоминаются и передаются расстояния, между опорными точками в виде матрицы расстояний, программе расчета оптимальной траектории.
Модель может функционировать в двух режимах: ручном и автоматическом.
Возможные состояния в автоматическом режиме: пуск, останов, сброс.
В ручном режиме могут задаваться:
- опорные точки траектории,
- курсовая скорость,
- величина наброса скорости,
- условия остановки движения (при попадании в заданную область одновременно по двум координатам или остановка отдельно по каждой из них),
- алгоритм управления (релейный закон, модифицированный релейный закон допускающий значение V=0, алгоритм следящей системы),
- тип фильтра (на основе вычисления регрессии, если помехи воздействуют непосредственно на робот, или сглаживание ошибок датчика определения координат маяка),
- уровень помехи.
В любом режиме интерфейс модели отображает состояния робота на каждом шаге его движения, указываются его координаты и отклонения от истинной траектории движения, показывается работа фильтра с учётом наложенного уровня помехи.
Также на экране отображается матрица расстояний между точками и полученная последовательность оптимальной траектории движения.
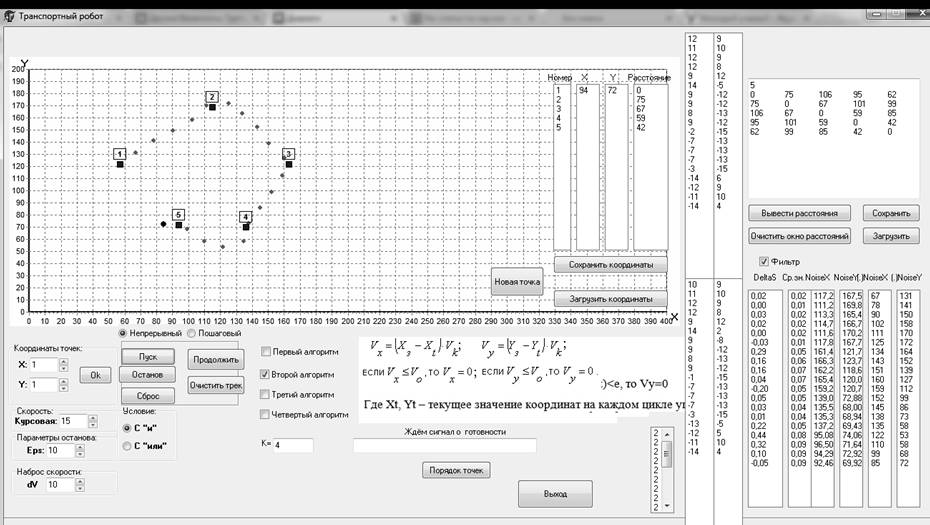
Рис. 3. Интерфейс программы Робот
Движение робота происходит в декартовой системе координат, где робот из начальной точки движется последовательно по всем заданным опорным точкам до достижения конечной точки (рис.4). Длина пути в данном случае равна 199.
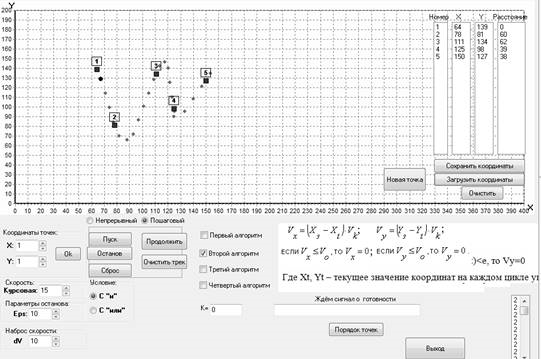
Рис. 4. Траектория движения робота (с начальным расположением точек)
Оптимальная последовательность движения робота по заданным точкам выдаётся в программу Робот (рис.5). Длина пути равна 188. Данная последовательность действий повторяется при обнаружении новых опорных точек.
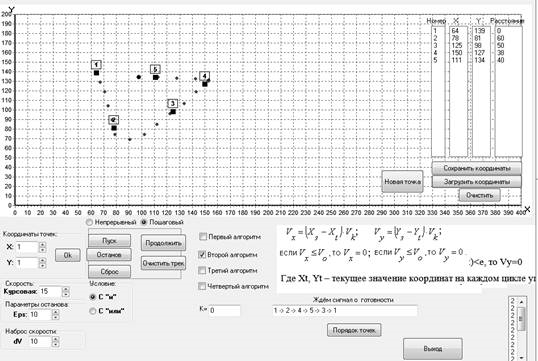
Рис. 5. Траектория движения робота (с оптимальным обходом)
На качество управления оказывают влияние внешние воздействия и ошибки датчиков робота. Ошибки датчиков не позволяют точно определить положение контрольных пунктов (КП) и вызывают ошибочное вычисление вектора скорости системой управления.
Ошибки могут быть связаны с неконтролируемым смещение робота за счет, например, ветра, наклона плоскости, по которой движется робот и т. п.
Очевидно, что для датчиков, измеряющих в полярных координатах, при приближению к КП ошибка управления будет уменьшаться, что видно из формулы
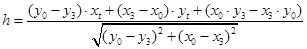 ,
,
где
h — отклонение от заданной траектории,
X0, Y0, X3, Y3 — координаты начальной и конечной точек на данном участке траектории,
Xt, Yt — текущие координаты.
Для датчиков, работающих в Декартовой системе, ошибка будет увеличиваться при приближении к точке Х3, У3 за счет угловой ошибки измерения пеленга на опорную точку.
Эти особенности следует учитывать при синтезе системы фильтрации помех.
Для решения поставленной задачи движения по заданным координатам был разработан соответствующий алгоритм. Робот оснащён датчиком радиально-кругового видения, когда робот проходит первый раз по линии датчик видит определённый набор точек (маяков), и следует в соответствии с полученной информацией. После расчётов оптимальной траектории в программе «Выбор оптимальной траектории движения», приложение «Транспортный робот» запускается для проверки. В результате могут быть обнаружены точки, которые датчик не распознал раньше. В этом случае необходимо заново рассчитать оптимальный путь уже с учётом новой точки. Если на робот наложены помехи (т. е. уровень помехи не равен нулю), то на каждом шаге движения робота в программе отображается отклонение робота. Данный алгоритм позволяет исследовать движение транспортного робота при априорной недостаточности информации и при наличии помех.
Разработанная модель позволяет задавать:
- произвольную конфигурацию КП и их количество,
- фиксированную курсовую скорость,
- инерционность робота, за счет величины наброса скорости (изменение скорости за цикл управления),
- уровень помехи,
- последовательность обхода точек, с учётом рассчитанного оптимального пути,
- размер матрицы (количество пунктов назначения),
- базовый пункт (из которого начнется оптимальный путь обхода),
- метод расчета оптимальной траектории.
Заключение
Разработана программная модель транспортного робота, движущегося по квазиоптимальной траектории для лабораторной работы по дисциплине «Моделирование робототехнических систем». Модель позволяет проводить исследования движения робота, при наличии помех и априорной недостаточности информации.
Литература:
1. Академия робототехники [Электронный ресурс] // Типы соревнований. –Электрон. дан. — [Б. м.], 2014. — URL: http://akarobo.ru/node/1 (дата обращения: 10.11.14)
2. Роботы, робототехника, микроконтроллеры [Электронный ресурс] // Регламенты соревнований роботов. — Электрон. дан. — [Б. м.], 2012. — URL: http://myrobot.ru/sport/index.php?n=Reglaments.HomePage (дата обращения: 4.11.14)
3. Раводин О. М., Давыдова Е. М. Моделирование системы управления устройства ЧПУ/ Интеллектуальные системы в управлении, конструировании и образовании/ под ред. А. А. Шелупанова.- Томск: SST, 2001.- 224с. УДК 06061201 ISBN 5–89503–078–52.
4. Раводин О. М., Бейнарович В. А. Принципы построения программного обеспечения копировально-фрезерных станков. // Аппаратно-программные средства автоматизации технологических процессов, -Изд-во ТУСУР. — Томск, 1998.
5. Раводин О. М.// Гибкие производственные системы и робототехника. -Учебное пособие. Издание 2-ое переработанное и дополненное. — Томск: В-Спектр, 2007. — 260с.







