В данной работе исследовано характеристики солнечных опреснительных установок. На основе тепловой схемы опреснителя записано дифференциальные уравнения теплового баланса и решено с методом преобразования Лапласа. Для решения полученных алгебраических систем уравнений использовано метод итерации. Создан алгоритм вычисления и разработан программное обеспечение в программном пакете Mathcad 2001 professional.
Получение питьевой воды за счет использования солнечной энергии, является одним из перспективных направлений возобновляемых источников энергии. Как известно, теоретическое исследование тепло и массообменных процессов солнечных опреснительных установок позволяет, определит оптимальные тепловые режимы и геометрические параметры и соответственно сэкономит время и материальные ресурсы для многочисленных экспериментов.
В настоящее время многие ученые в мире ведут фундаментальные и практические исследования по сфере солнечных водоопреснительных установок [1–5].
Теоретическая часть
Для математического моделирования тепловых и массообменных процессов солнечных опреснительных установок (тепловая схема приведена на рис.1) записывается уравнения теплового баланса для каждого элемента:
уравнения теплового баланса для прозрачной части (стекло) установки
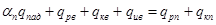, (1)
уравнения теплового баланса для воды находящийся внутри установки
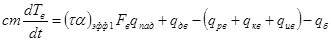, (2)
где, Тв- температура воды, °С; Fв- поверхность воды, м2; qпад- падающая суммарная солнечная радиация, Вт/м2; t- время, с; (ta)эфф1- эффективный коэффициент поглощения солнечной радиации воды; с- удельная теплоемкость воды, Дж/(кг×град); m- масса воды, кг;
уравнения теплового баланса дна установки
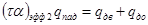. (3)
Плотности теплового потока, приведенные в уравнениях (1)-(3) определяются следующими уравнениями:
плотность теплового потока с излучением от воды к прозрачной среде (стекло) установки
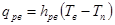, (4)
где, Тп — температура прозрачной среды (стекло),°С; hрв- коэффициент теплообмена с излучением от воды к прозрачной среде, Вт/(м2×град).
плотность теплового потока с конвекцией от воды к прозрачной среде (стекло) установки
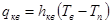, (5)
плотность теплового потока с испарением от воды к прозрачной среде (стекло) установки
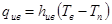, (6)
плотность теплового потока с излучением от прозрачной среде (стекло) к окружающей среде
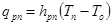, (7)
плотность теплового потока с конвекцией от прозрачной среды (стекло) к окружающей среде
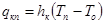, (8)
плотность теплового потока от воды к окружающей среде
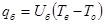, (9)
плотность теплового потока с конвекцией от дна установки к воде
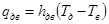, (10)
плотность теплового потока от дна установки к окружающей среде
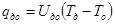. (11)
Решая уравнения (1) и (3) относительно Тп и Тд получаем следующие
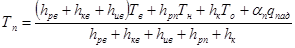, (12)
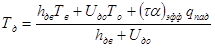. (13)
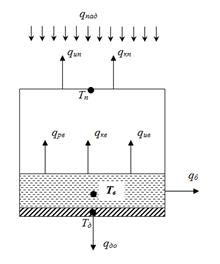
Рис.1. Тепловая схема солнечной водоопреснительной установки.
Уравнения (2), после некоторых преобразований будет решено с помощью метода Лапласа
,
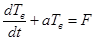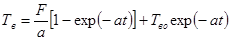, (14)
где,
,
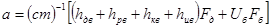F=(cm)-1 [(ta)эфф1Fбqпад+FдhдвTд+(hрв+hкв+hив)FвTп+UбFбTо].
Решая уравнения (12), (13) и (14) с методом итерации можно определить температуры элементов установки.
Коэффициенты теплоотдачи определяются следующими уравнениями [6,7]:
коэффициент теплоотдачи с конвекцией между водой и прозрачной средой
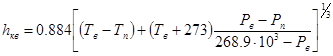, (15)
,
,
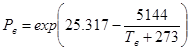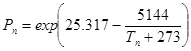коэффициент теплоотдачи с излучением между водой и прозрачной средой
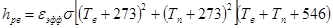, (16)
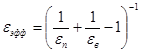, (17)
коэффициент теплоотдачи с испарением между водой и прозрачной средой
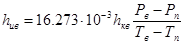(18)
Масса конденсата определяется следующими уравнениями
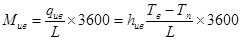. (19)
Коэффициент теплоотдачи с излучением от прозрачной среды к окружающей среде
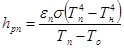, (20)
где, Тн=To [0.711+0.0056Tтр+0.000073Ттр2+0.013cos(15t)]1/4 (22)
температура небосвода.
Коэффициент теплоотдачи с конвекцией от прозрачной среды к окружающей среде
hк=2.8+3.0×V. (23)
Коэффициент теплопередачи от воды к окружающей среде
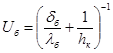. (24)
Коэффициент теплопередачи от дна установки к окружающей среде
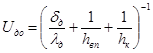. (25)
Методика проведения расчетов и результаты
Геометрические и теплотехнические параметры установки приведены в таблице 1.
Таблица 1
Геометрические и теплотехнические параметры установки
|
Параметры |
Значение |
|
Fп |
3м2 |
|
Fб |
0.35 м2 |
|
Fв= Fд |
2.5 м2 |
|
eп |
0.9 |
|
eв |
0.9 |
|
aп |
0.05 |
|
aв |
1-ехр(-bdв) |
|
aд |
0.9 |
|
L |
2022×103 Дж/кг |
|
dб |
1.2 мм |
|
dд |
1.2 мм |
|
lб, |
14.4 Вт/м |
|
lд |
14.4 Вт/м |
|
s |
5.67×10–8 Вт/м2 |
Суммарная солнечная радиация, падающая на поверхностях установки, определено с методом приведенной в [6].
Расчеты проведены в пакете Mathcad 2001 professional.
Температура окружающей среды и падающая суммарная солнечная радиация приведено в рис.2.
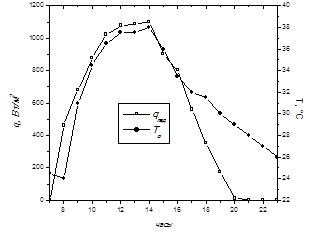
Рис. 2. Температура окружающей среды и падающая суммарная солнечная радиация
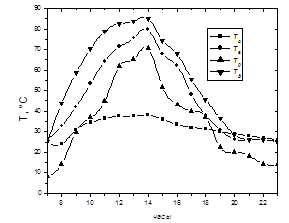
Рис. 3. Расчетные результаты температура воды, дна установки и прозрачной среды
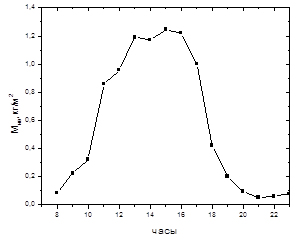
Рис. 4. Расчетные результаты часовые значения массы конденсата.
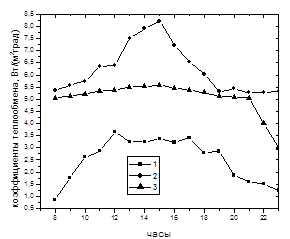
Рис. 5. Суточные изменения коэффициентов теплообмена, 1- коэффициент теплоотдачи с конвекцией между водой и прозрачной средой; 2-коэффициент теплоотдачи с излучением между водой и прозрачной средой; 3-коэффициент теплоотдачи с конвекцией от дна установки к воде.
Как видно из рис.3 максимальное значения температуры воды внутри установки достигает до 80°С и соответственно суточное значения массы полученного конденсата 8.17 кг (рис.4).
Выводы
Проведенные теоретические исследования позволяют сделать следующие выводы:
- уравнения (12)-(14), полученные методом Лапласа дают возможность оценить температурный и рабочий режим солнечных опреснительных установок;
- используя уравнение (19) можно определить суточную массу конденсата;
- изменяя граничные условия, приведенные на рис.2, можно оценить рабочий режим солнечной опреснительной установки любого дня года.
Литература:
1. Dimri V., Sarkar B., Singh U., Tiwari G. N. Effect of condensing cover material on yield of an active solar still: an experimental validation, Desalination 227 (2008) 178–189.
2. Phadatare M. K., Verma S. K. Influence of water depth on internal heat and mass transfer in a plastic solar still, Desalination 217 (2007) 267–275.
3. Авезов Р. Р., Ахатов Ж. С. Коэффициент использования тепла солнечных водоопреснительных установок с многоступенчатыми испарительно-конденсационными камерами // Гелиотехника. 2007. № 2. С. 3–7.
4. Авезов Р. Р., Клычев Ш. И., Ахатов Ж. С. Расчетно-экспериментальное исследование теплотехнических характеристик многоступенчатой испарительно-конденсационной камеры солнечной опреснительной установки // Гелиотехника. 2005. № 3. С. 30–34.
5. Клычев Ш. И., Эркинбаева Г., Бахрамов С. А., Исманжанов А. А. Теплотехнические характеристики солнечных парниковых опреснителей. // Гелиотехника. 2002. № 2. С. 38–43.
6. Duffie J., Beckman W. Solar engineering of thermal processes. New York. Wiley, 1991. -919p.
7. Yunus A.Cengel. Heat and mass transfer: a practical approach. New York. McGraw-Hill, 2006. 853p.
