Рассмотрим собственные колебания в упругой среде, содержащей двухслойный цилиндрический слой в цилиндрической системе координат (r,z,θ). Обозначим через Vpi, Vsi, ri, μi, li (i =0,1,2,3) соответственно скорость продольной и поперечной волны, плотность и модуль упругости. Рассмотрим задачу о распространении свободных волн, возникающих в такой системе. Уравнения движения среды для продольных φi и поперечных ψi потенциалов представляется в виде:
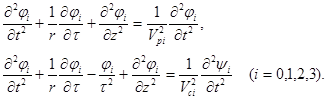(1)
В уравнениях (1) следует положить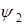 
=0, если в затрубном пространстве находится жидкость. Соответствующие напряжения srr, tir и смещения u r, u z, определяются через потенциалы j, y равенствами
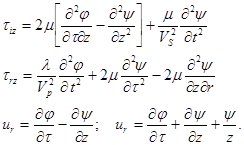(2)
На границах раздела упругой среды с жидкостью выполняются граничные условия непрерывности нормальных составляющих смещений и напряжений, а также равенство нулю касательных напряжений в твердом теле:
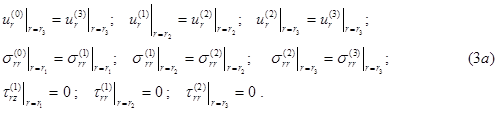
Если жидкость заменена упругой средой, то на контакте двух сред ставятся следующие условия:
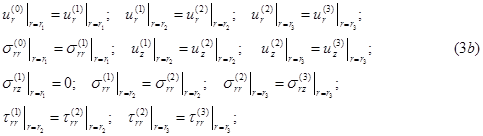
Решения уравнений (1), удовлетворяющих условию конечности среды на оси r=0 и условиям убывания на бесконечности, выражаются через модифицированные функции Бесселя.
На границе контакта слоев (r = r2) ставится условие скользящего контакта (непрерывны нормальные составляющие напряжений и смещений, отсутствуют касательные составляющие напряжений) и контакт между внешним слоем и окружающей средой жесткий (непрерывны нормальные и тангенциальные составляющие напряжений и смещений). Дисперсионное уравнение записывается в виде:
D(к, h)=0. (4)
Оно представимо в виде определителя, у которого элементы dij (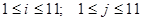
), отличные от нуля, имеют следующий вид:
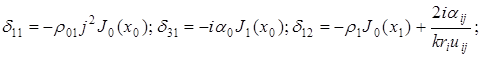
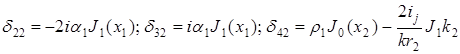
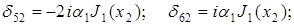
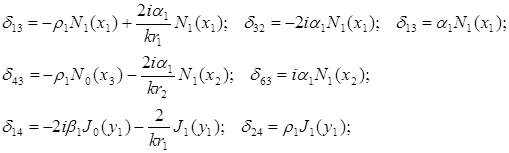
Остальные элементы также записываются в аналогичном виде. Здесь
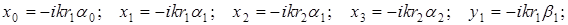
в двухслойном цилиндре V определяет скорость обобщенной волны по двухслойному цилиндру. Фазовая скорость волны определятся величиной реальной части корня, то есть Vj = ReV; величины мнимой части корня связаны с затуханием c на единице расстояния зависимостью
.
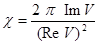Дисперсионное уравнение (4) решается методом Мюллера. Значение левой части на каждой итерации метода Мюллера определяется методом Гаусса с выделением главного элемента. Нами были составлены программы и проведены расчеты дисперсии и затухания волны Лэмба для моделей скважин, описываемых граничными условиями (3а) и (3b). Исходя из физической постановки задачи, будем считать, что поглощением обладают буровая жидкость, цемент, тампонажная смесь, поглощением же в материале колонны и в окружающей среде будем пренебрегать. Переход к системе с поглощением был сделан посредством введения комплексных параметров сред. Численные результаты получены при следующих значениях параметров:
Vp0 =1500 м/c; Vp0 =1500 м/c; Vp2 =1500 м/c;
Vp3 =5300 м/c; Vs1 =2900 м/c; Vs2 =2000 м/c;
Vs3 =2000 м/c; ρ0 =1 г/cм3; ρ1 =8 г/cм3;
Ρ2 =3 г/cм3; ρ4 =4 г/cм3; r1 =0,05 м; r2 =0,06 м; r3 =0,067 м.
Результаты расчетов представлены в табл. 1. Видно, что фазовая скорость слабо зависит от волнового числа.
Таблица 1
Изменение фазовой скорости V (м/c) в зависимости от волнового числа α/a.
|
α/a |
1 |
2 |
3 |
4 |
5 |
|
1 |
1450,121 |
1450,024 |
1451,01 |
1456,28 |
1450,82 |
|
2 |
1456,3 |
1456,09 |
1456,013 |
1456,72 |
1455,3 |
|
3 |
1462,24 |
1462,50 |
1462,03 |
1462,4 |
1461,9 |
Из анализа значений фазовой скорости выявлено, что разница между скоростями осесимметричных и не осесимметричных волн первой моды мала для всех значений волнового числа, кроме близких к нулю (область очень длинных волн), а минимумы части первой моды для всех значений n совпадают, так что и в данном случае первая резонансная скорость может быть определена из решения соответствующей осесимметричной задачи. Так при γ>250 получено С=0,31 (3ρ/G)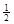
. Как показали расчеты, наименьший вклад дает поглощение продольной волны (рис. 1).
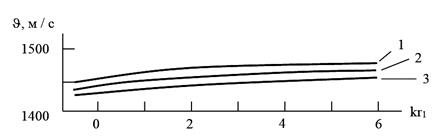
Рис. 1. Зависимости фазовой скорости от волнового числа.
Из результатов выясняется, что сжимающие контактные напряжения имеют место в некоторой окрестности приложения каждой силы. С удалением от точки приложения силы по окружности напряжения для всех рассмотренных случаев меняют знак. Это является следствием предположения двухсторонних характеров связи между оболочкой и заполнителем.
Литература:
1. Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. — Ташкент; Фан, 1992. — 250 с.
